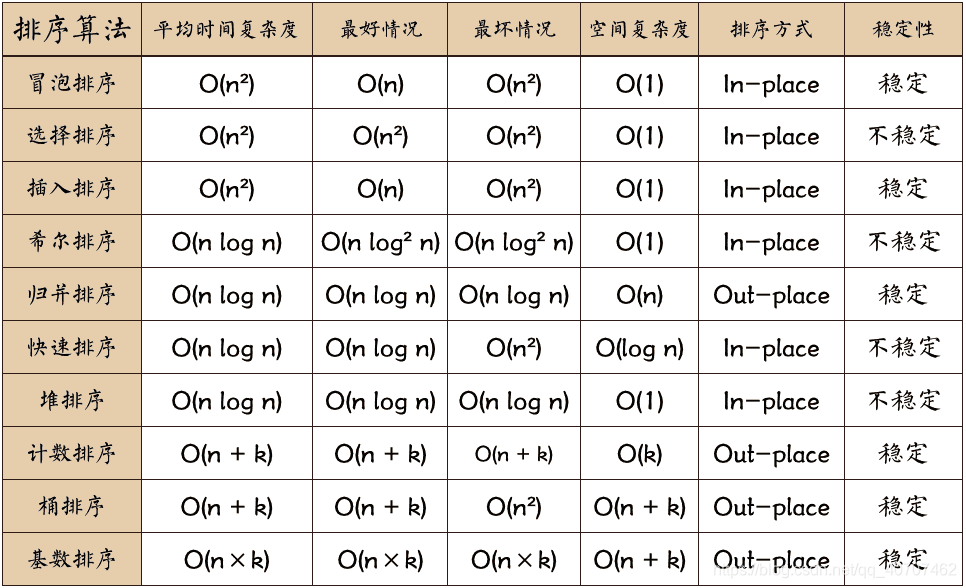
(从小到大)
①直接插入
- (第一层循环)从第一个元素i开始
- (第二层循环)取出i的下一个数,向前遍历,如果比前一个数小,就换位

public static void sort(int[] a) {
for (int i = 0; i < a.length - 1; i++) {
for (int j = i + 1; j > 0; j--) {
if (a[j] < a[j - 1]) {
int temp = a[j];
a[j] = a[j - 1];
a[j - 1] = temp;
}
}
}
}
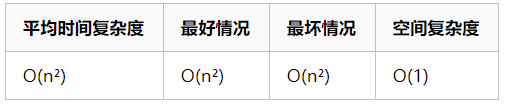
②简单选择
- (第一层循环)i遍历
- (第二层循环)从未排序序列中(i之后),找到最小的元素min,如果最小元素不是未排序序列的第一个元素(i),则min和i互换
public static void sort(int[] a) {
for (int i = 0; i < a.length; i++) {
int min = i;
//选出之后待排序中值最小的位置
for (int j = i + 1; j < a.length; j++) {
if (a[j] < a[min]) {
min = j;
}
}
//最小值不等于当前值时进行交换
if (min != i) {
int temp = a[i];
a[i] = a[min];
a[min] = temp;
}
}
}
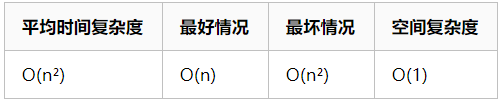
③冒泡排序
- (第一层循环)取出每个数i准备比较,只需要比较n-1个数,每次可以固定在末尾一个最大的数
- (第二层循环)每次从第一个数起比较相邻的元素。如果第一个比第二个大,就交换他们两个。从开始第一对到结尾的最后一对,一共需要比较n-i-1次(i次就代表已经固定了最大i个元素)。这步做完后,最后的元素会是最大的数。
public static void sort(int[] a) {
//外层循环控制比较的次数
for (int i = 0; i < a.length - 1; i++) {
//内层循环控制到达位置
for (int j = 0; j < a.length - i - 1; j++) {
//前面的元素比后面大就交换
if (a[j] > a[j + 1]) {
int temp = a[j];
a[j] = a[j + 1];
a[j + 1] = temp;
}
}
}
}
④快速排序(双路)
- 从数列中挑出一个元素,称为"基准"(pivot)。
- 重新排序数列,所有比基准值小的元素摆放在基准前面,所有比基准值大的元素摆在基准后面(相同的数可以到任一边)。在这个分区结束之后,该基准就处于数列的中间位置。这个称为分区(partition)操作。
递归地把小于基准值元素的子数列和大于基准值元素的子数列排序。
伪代码:
- i = L; j = R; 将基准数挖出形成第一个坑a[i]。
- j- -,由后向前找比它小的数,找到后挖出此数填前一个坑a[i]中。
- i++,由前向后找比它大的数,找到后也挖出此数填到前一个坑a[j]中。
- 再重复执行2,3二步,直到i==j,将基准数填入a[i]中
虽然 Worst Case 的时间复杂度达到了 O(n2),但是人家就是优秀,在大多数情况下都比平均时间复杂度为 O(n logn) 的排序算法表现要更好。
public static void sort(int[] a, int low, int high) {
//已经排完
if (low >= high) {
return;
}
int left = low;
int right = high;
//保存基准值
int pivot = a[left];
while (left < right) {
//从后向前找到比基准小的元素
while (left < right && a[right] >= pivot)
right--;
a[left] = a[right];//此时right后面的都比他大
//从前往后找到比基准大的元素
while (left < right && a[left] <= pivot)
left++;
a[right] = a[left];//此时left前面的都比他小
}
// left=right,放置基准值,准备分治递归快排
a[left] = pivot;
sort(a, low, left - 1);
sort(a, left + 1, high);
}
⑤归并排序
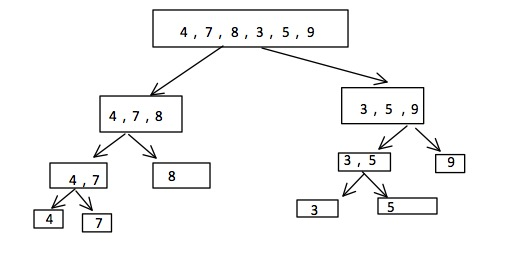

def sort(lst, low, mid, high):#合并
i = low
j = mid +1 # low到mid 代表了前面所有拍好序的一个组,mid 到 mid + 1 是乱序部分 mid+1 到最后又是另一个排好序的组
lstm = []
while i <= mid and j <= high:
if lst[i] < lst[j]: #比较两个指针指向的数的大小,把小的一个append到新列表, 并且谁放进去了,谁索引自增一
lstm.append(lst[i])
i += 1
else:
lstm.append(lst[j])
j += 1
# 出现 某一边,可能是左边可能是右边先排完了,将剩下的有序数全部处理添加到新列表
while i <= mid:
lstm.append(lst[i])
i += 1
while j <= high:
lstm.append(lst[j])
j += high
lst[low: high+1] = lstm #最后将拍好序新列表的,赋值回传入的列表的索引段
def merge_sort(lst, low, high):#分治
if low < high:
mid = (low + high) // 2
merge_sort(lst, low, mid)
merge_sort(lst, mid + 1, high)
sort(lst, low, mid, high) # 开始排序
list=[5,4,5,6,6,5,4,4,1,1,22,3,2]
n=len(list)
merge_sort(list,0,n-1)
print(list)
⑥堆排序
大根堆:每个结点的值都大于或等于左右孩子结点
小根堆:每个结点的值都小于或等于左右孩子结点
步骤:
- 首先将待排序的数组构造出一个
大根堆 - 取出这个大根堆的堆顶节点(最大值),与堆的最下最右的元素(即最小值)进行交换,然后把剩下的元素再构造出一个大根堆
(此时最大值在数组末尾,以后建堆不再用它了) - 重复第二步,直到这个大根堆里的数被取完,此时被取出的数完成
从小到大排序。
构建大根堆:
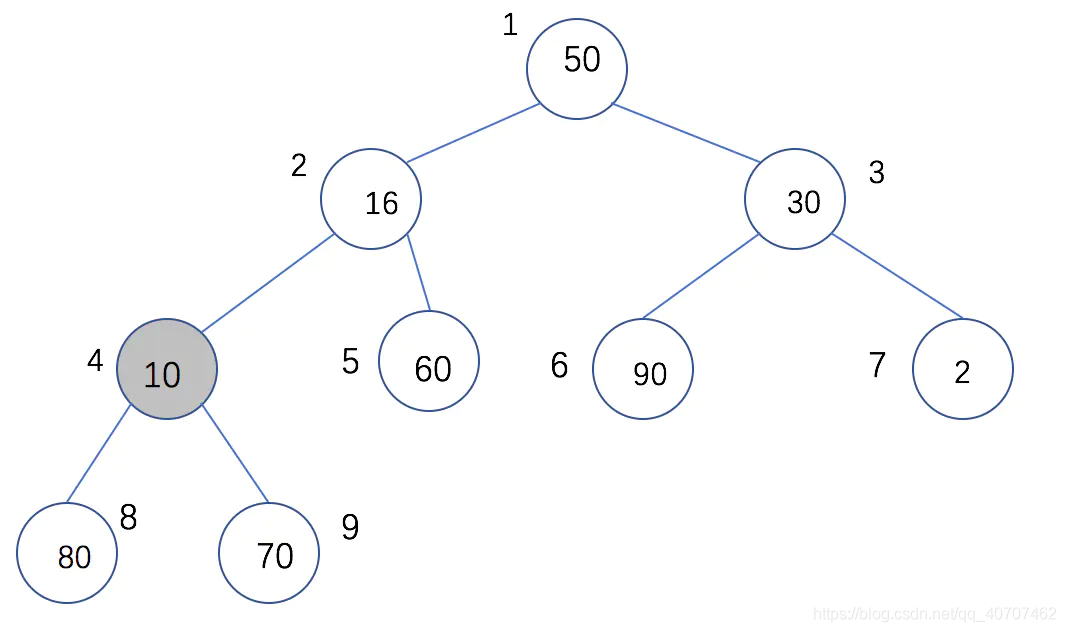
- 构造堆排序从
end // 2 - 1开始倒序,意思是找到每个有子节点的节点,调整每个小树,使它符合大顶堆 - 构建大根堆就是每个子树的根节点和较大的子节点进行值交换
def heap_sort(alist):
def siftdown(alist,begin, end): # 向下筛选
e=alist[begin]#e是最小值,处在堆顶
i, j = begin, begin * 2 + 1 # j为i的左子结点
while j < end:
if j + 1 < end and alist[j] < alist[j + 1]: # 如果左子结点小于右子结点
j += 1 # 则将j指向右子结点
if e > alist[j]: # j已经指向两个子结点中较大的位置,
break # 如果插入元素e大于j位置的值,则为3者中最大的
alist[i] = alist[j] # 能执行到这一步的话,说明j位置元素是三者中最大的,则将其上移到父结点位置
i, j = j, j * 2+1 # 更新i为被上移为父结点的原来的j的位置(左子节点),更新j为更新后i位置的左子结点
alist[i] = e # 如果e已经是某个子树3者中最大的元素,则将其赋给这个子树的父结点
end = len(alist)
for i in range(end // 2 - 1, -1, -1): # 构造堆序。
siftdown(alist, i, end)
for i in range((end - 1), 0, -1): # 进行堆排序.i最后一个值为1,不需要到0
alist[i],alist[0] = alist[0],alist[i] # 交换堆顶与最后一个元素
siftdown(alist, 0, i)
return alist
if __name__ == "__main__":
alist = [4,10,3,5,1]
print(alist)
heap_sort(alist)
print(alist)