[数据结构与算法]LeetCode 力扣周赛 256 题解

最近一直打的很烂，赛前安慰自己只要三道题不出错就算进步，结果只做出来两道题，要被自己蠢哭了。

你说是题目变难了吧，老铁们都唰唰的过题。说是自己变菜了吧，这水平下降的也太快了点，照这样下去，下次只能出一道题了。

想了半天，只能是题目变难了，老铁们也变强了，只有我留在原地了，真的太难了。

5854. 学生分数的最小差值

思路：排序，枚举

时间复杂度：$O(n\lg n)$

首先将 nums 升序排序，则答案为：
$$\underset{0\le i<n?k+1}{\min }(nums[i+k?1]?nums[i])$$

class Solution {
public:
    int minimumDifference(vector<int>& nums, int k) {
        sort(nums.begin(), nums.end());
        int anw = nums[k-1] - nums[0];
        for (int i = 1; i+k-1 < nums.size(); i++) {
            anw = min(anw, nums[i+k-1] - nums[i]);
        }
        return anw;
    }
};

5855. 找出数组中的第 K 大整数

思路：排序

时间复杂度：$O(n\lg n)$

因为输入数据不含前导零，所以长字符串对应的数字一定比短字符串的大。因此，可以先通过二级排序将 nums 降序排序，排序后的 nums[k-1] 即为答案。

二级排序规则为：

• 长度不同的按长度降序排序
• 长度相同的按字典序降序排序

class Solution {
public:
    string kthLargestNumber(vector<string>& nums, int k) {
        sort(nums.begin(), nums.end(), [](const auto &l, const auto &r) -> bool {
            if (l.size() != r.size()) {
                return l.size() > r.size();
            }
            return l > r;
        });
        return nums[k-1];
    }
};

5856. 完成任务的最少工作时间段

思路：位运算，动态规划，枚举子集

时间复杂度：$O(n?2^n+3^n)$

设有长度为 $2^n$ 的数组 $dp$，$d{p}_{mask}$ 表示任务完成状态为 $mask$ 时的最小花费。

任务完成状态 $mask$ 可理解为由 $n$ 个比特表示的集合，从低位到高位，如果第 $i$ 位比特为 1，则表示 $tas{k}_i$ 已完成，反之未完成。

显然，状态 $mask$ 可划分为两个子状态 $a$ 和 $b$，满足：

• $a\&b=0$
• $a|b=mask$

换言之，$mask$ 中为 1 的比特，仅在 $a$ 或 $b$ 中的一个为一，另一个为零。

于是，得到了状态转移方程：
$$d{p}_{mask}=\underset{a\&b=0,a|b=mask}{\min }(d{p}_a+d{p}_b)$$

特别的，当 $mask$ 代表的任务集合的耗时不超过 $sessionTime$ 时，$d{p}_{mask}=1$。

如何枚举 $a$ 和 $b$

给定 $mask$，可通过下述方式枚举 $a$ 和 $b$。

for (int a = mask, b = 0; a > b; a = (a-1)&mask, b = a^mask) {
  // do something
}

其中关键在于 a=(a-1)&mask。

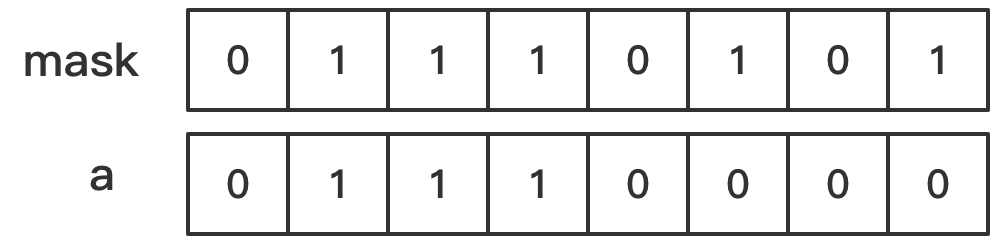
设有 $a$ 和 $mask$ 的值如上所示，减法运算和与运算对 $a$ 的影响如下图示：

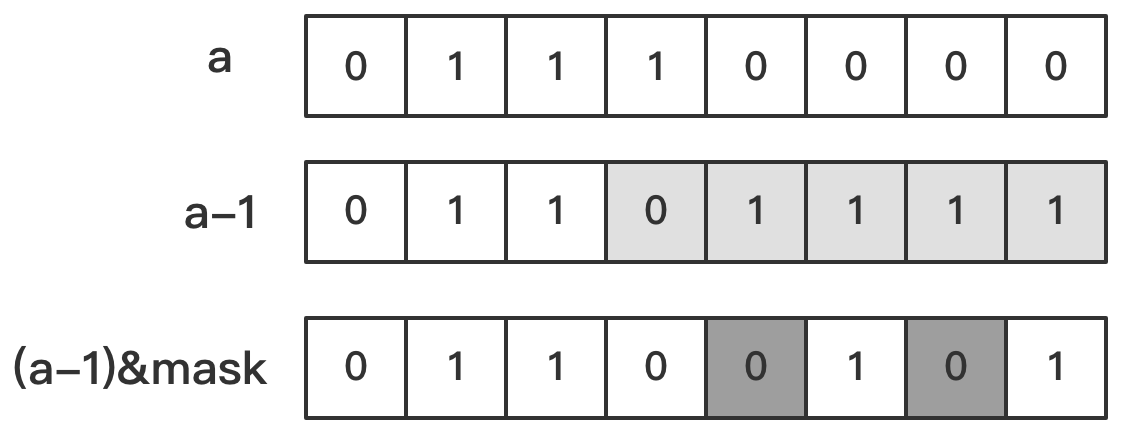
减法运算将 $a$ 中「值为 1 」的「最低位」的比特置为 0，并将其后的 0 全置为 1。

与运算将不应变为 1 的比特再置回 0。

这套组合拳可理解为：将 $a$ 中那些「在 $mask$ 中的对应比特为 0」的比特删去，然后做减法，这显然可以枚举出 $mask$ 的所有子集。

一个小剪枝

设初始时，$a=mask,b=0$。随着枚举进行，必然会从 $a\ge b$ 变为 $a<b$。显然此时没必要继续枚举下去了，因为 $(a,b)$ 和 $(b,a)$ 是对称的。

时间复杂度

对于包含 $n$ 个比特且恰有 $k$ 个比特为 1 的 $mask$，共有 $2^k$ 个子集，这样的 $mask$ 共有 $C_n^k$ 个。因此整体的计算量可用 $(2+1{)}^n$ 的二项式展开来表示：
$$

\begin{align*}
\sum_{k=0}^{n}C_nk2^k&= \sum_{k=0}^{n} C_n^k*2k1^{n-k} \
&= (2+1)^n \
&= 3^n \
\end{align*}
$$

class Solution {
public:
    int minSessions(vector<int>& tasks, int sessionTime) {
        int n = tasks.size();
        int m = (1<<n);
        vector<int> sum(m, 0);
        for (int i = 1; i < m; i++) {
            for (int j = 0, b = 1; ; b <<= 1, j++) {
                if (i&b) {
                    sum[i] = sum[i^(b)] + tasks[j];
                    break;
                }
            }
        }

        vector<int> dp(m, numeric_limits<int>::max());
        dp[0] = 0;
        for (int i = 1; i < m; i++) {
            if (sum[i] <= sessionTime) {
                dp[i] = 1;
            } else {
                for (int a = i, b = 0; a > b; a = (a-1)&i, b = a^i) {
                    dp[i] = min(dp[i], dp[a] + dp[b]);
                }
            }
        }
        return dp[m-1];
    }
};

1987. 不同的好子序列数目

思路：动态规划，滚动数组，去重

时间复杂度：$O(n)$

假设我们现在有两个集合 $zero$ 和 $one$，分别由 ‘0’ 开头的序列和 ‘1’ 开头的序列组成，且其中无重复序列。

现在我们要向所有序列的前面加 ‘1’，构成新的集合 $on{e}^{\prime }$ 包含：

• $|zero|$ 个以 ‘10’ 开头的序列
• $|one|$ 个以 ‘11’ 开头的序列

因为 $one$ 和 $zero$ 本身无重复，所以 $on{e}^{\prime }$ 也无重复。另外，$on{e}^{\prime }$ 中的序列长度均大于一，所以将 ‘1’ 插入 $on{e}^{\prime }$ 中仍不会有重复。

除了证明 $on{e}^{\prime }$ 本身无重复外，还需证明 $one?on{e}^{\prime }$，考虑 $one$ 中的三类序列：

• 以 ‘10’ 开头，必然由 $zero$ 的某个子集添加 ‘1’ 而来，这部分必然在 $on{e}^{\prime }$ 中。
• 以 $11$ 开头，必然由 $one$ 的某个子集添加 ‘1’ 而来，这部分必然也在 $on{e}^{\prime }$ 中。
• ‘1’ 本身，我们向 $on{e}^{\prime }$ 添加了 ‘1’，所以该序列也在 $on{s}^{\prime }$ 中。

所以，$one?on{e}^{\prime }$

所以有，$|on{e}^{\prime }|=|zero|+|one|+1$。

同理，向所有序列的前面加 ‘0’，构成的新集合 $zer{o}^{\prime }$ 包含：

• $|zero|$ 个以 ‘00’ 开头的序列
• $|one|$ 个以 ‘01’ 开头的序列

同样的，也可将 ‘0’ 插入 $zer{o}^{\prime }$ 中。

因此，$|zer{o}^{\prime }|=|zero|+|one|+1$

class Solution {
public:
    int numberOfUniqueGoodSubsequences(string binary) {
        int zero = 0, one = 0; // 初始时均为空集合
        int mod = 1e9+7;
        int has_zero = 0; // 判断是否幽灵
        for (int i = binary.size()-1;i >= 0; i--) {
            if (binary[i] == '0') {
                has_zero = 1;
                zero = (zero + one + 1)%mod;
            } else {
                one = (one + zero + 1)%mod;
            }
        }
        return (one + has_zero) % mod;
    }
};