[数据结构与算法]LeetCode_单调栈_困难_84.柱状图中最大的矩形

1.题目

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。
求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1：

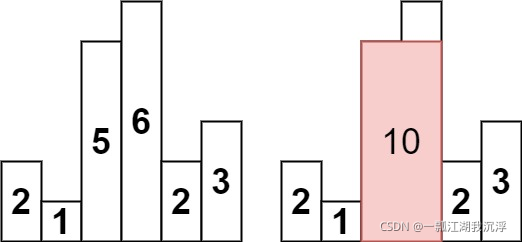
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

示例 2：

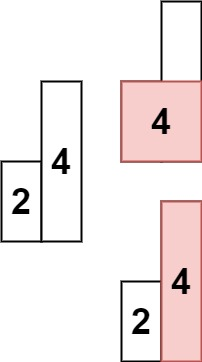
输入：heights = [2,4]
输出：4

提示：
1 <= heights.length <=10⁵
0 <= heights[i] <= 10⁴

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/largest-rectangle-in-histogram

2.思路

（1）单调栈
所谓单调栈，即元素值单调递增或单调递减的栈。单调栈这种数据结构，通常应用在一维数组上，如果需要解决的问题与前后元素之间的大小关系有关的话，此时可以考虑使用单调栈。例如在本题中，前后柱子的高度会影响最大矩形面积的计算。
（2）暴力穷举法
使用两层 for 循环穷举出所有的矩阵，然后保存最大面积并返回即可，但是该方法的时间复杂度较高，为O(n²)，所以在LeetCode中运行时存在超时现象，并不能通过。

3.代码实现（Java）

//（1）单调栈
public int largestRectangleArea(int[] heights) {
    int length=heights.length;
    //定义最大的矩形面积，初始值为0
    int maxArea=0;
    //定义单调栈，此处存储数组元素的下标，保证下标对应的值从栈底到栈顶逐渐递增
    Stack<Integer> stack = new Stack<>();
    for(int i=0;i<length;i++){
        //栈不为空，并且当前元素值小于等于数组下标为栈顶元素的值
        while(!stack.isEmpty() && heights[i]<=heights[stack.peek()]){
            //将栈顶元素出栈
            int j=stack.pop();
            //求左边界
            int left=stack.isEmpty()?-1:stack.peek();
            //矩形面积=(右边界-左边界-1)*高度
            int curArea = (i-left-1)*heights[j];
            maxArea = Math.max(maxArea, curArea);
        }
        //将当前下标加入到栈中
        stack.push(i);
    }
    //求整个高度单调递增的柱子所能勾勒出来的矩形的最大面积
    while(!stack.isEmpty()){
        int j=stack.pop();
        int left=stack.isEmpty()?-1:stack.peek();
        //此时的右边界就是数组长度
        int curArea=(heights.length-left-1)*heights[j];
        maxArea = Math.max(maxArea, curArea);
    }
    return maxArea;
}

//（2）暴力穷举法
public int largestRectangleArea(int[] heights) {
    int len=heights.length;
    int maxArea=heights[0];
    int minLength;
    //暴力穷举法
    for(int i=0;i<len;i++){
        minLength=heights[i];
        for(int j=i;j<len;j++){
            //求出当前矩阵的宽
            int width=(j>i)?(j-i+1):1;
            //求出当前矩阵的长，它由最小的柱子高度决定
            minLength=(heights[j]<minLength)?heights[j]:minLength;
            //求出当前矩阵的面积
            int curArea=width*minLength;
            //保存当前得到的最大矩阵面积
            maxArea=(maxArea>curArea)?maxArea:curArea;
        }
    }
    //返回最大面积
    return maxArea;
}