[数据结构与算法]【Java学习】顺序表和链表【详解篇9】

两个数据结构：顺序表和链表

• 数据结构是一门学科（逻辑很严谨的学科），和语言没有关系，如C语言数据结构和Java数据结构，这里的C语言和Java只是一门工具，我们只是通过某一种语言来学习这门学科。
• 数据+结构：一种描述和组织数据的方式。

那为甚麽有那么多的数据结构呢？

答：因为组织和描述数据的方式是不一样的，比如有些数据结构适合增、有些适合删、有些适合查、有些适合改等，所以才有了这么多的数据结构。

一、线性表

线性表（linear list）是n个具有相同特性的数据元素的有限序列。 线性表是一种在实际中广泛使用的数据结构，常
见的线性表：顺序表、链表、栈、队列、字符串…
线性表在逻辑上是线性结构，也就说是连续的一条直线。但是在物理结构上并不一定是连续的，线性表在物理上存
储时，通常以数组和链式结构的形式存储。

二、顺序表

概念及结构

顺序表是用一段物理地址连续的存储单元依次存储数据元素的线性结构（顺序表在逻辑上和物理上都是连续的），一般情况下采用数组存储。在数组上完成。顺序表从本质上来说就是一个数组。
数据的增删查改。
顺序表一般可以分为：
静态顺序表：使用定长数组存储。
动态顺序表：使用动态开辟的数组存储。
静态顺序表适用于确定知道需要存多少数据的场景.
静态顺序表的定长数组导致N定大了，空间开多了浪费，开少了不够用.
相比之下动态顺序表更灵活, 根据需要动态的分配空间大小.

接口实现

实现一个动态顺序表. 以下是需要支持的接口.

public class TestSequenceList {
    public void display(){   }   //打印顺序表
    public void add(int pos,int data){    }  //在pos位置新增元素
    public boolean contains(int toFind){return true ;}  //判定是否包含某个元素
    public int search(int toFind){return -1;} //查找某个元素对应的位置
    public int getPos(int pos){return -1;} //获取pos位置的元素
    public void setPos(int pos,int value){  } //给pos位置的元素设置为value
    public void remove(int toRemove){  }//删除第一次出现的关键字key
    public int size(){return 0;} //获取顺序表长度
    public void clear(){  }//清空顺序表
}

在实现接口之前我们先通过画图举一个例子来理解一下实现的思路

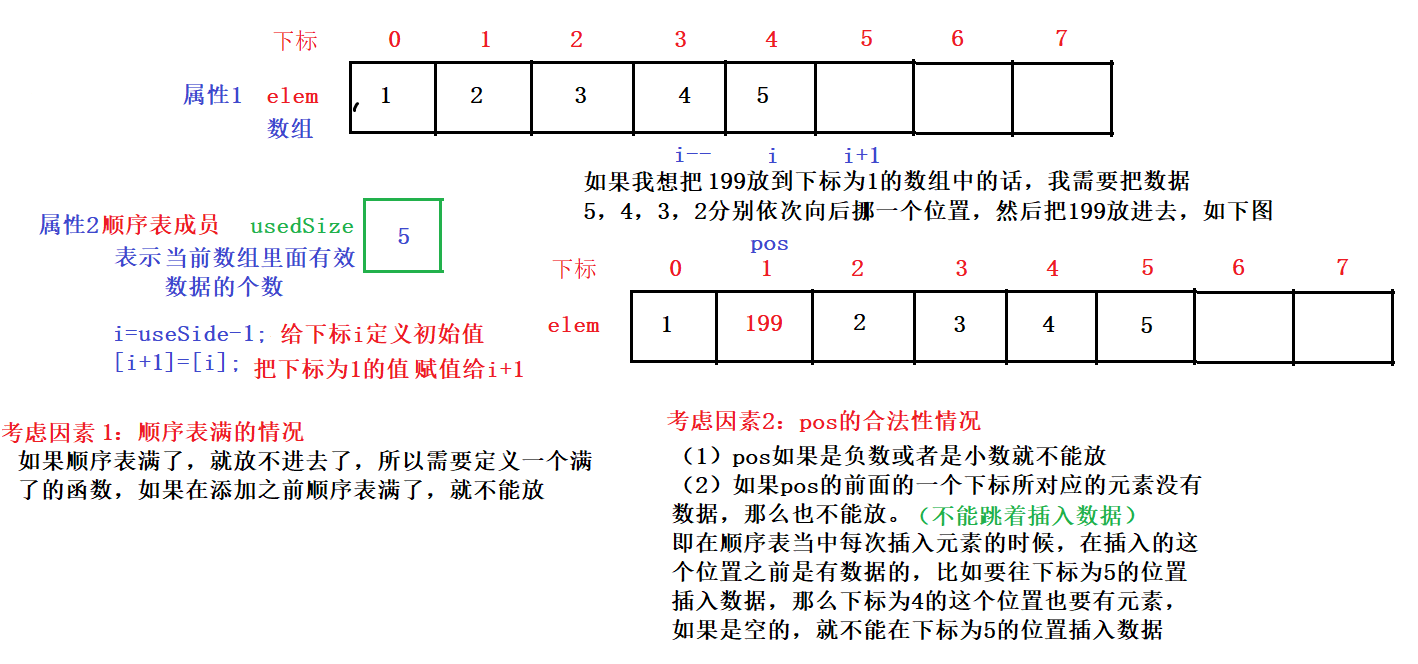
顺序表接口的实现代码

public class MyArrayList {
    public int[] elem;//elem=null
    public int usedSize;

    public static int capacity=10;//capacity=10不能改变，所以需要写一个static final
    public MyArrayList(){//构造方法
        //elem是一个数组，它需要初始化，如果不初始化的话它就会默认为null
        //usedSide可以不初始化，默认为0

        //this.elem=new int[10];//可以这样初始化elem
        this.elem=new int[capacity];//可以这样初始化elem
    }
    public boolean isFull(){//顺序表满的情况
        if(this.usedSize==capacity){
            return true;
        }
        return false;
        //return this.usedSize==capacity;也可直接写成一句
    }
//在pos位置新增元素
    public void add(int pos,int data){  //在pos位置新增元素:给你一个下标pos，然后把data数据放到对应下标里
        //pos的合法性
        if(pos<0 || pos>this.usedSize){
            System.out.println("pos的插入位置不合法");
        }
        if (isFull()) {//满了，需要扩容
            this.elem= Arrays.copyOf(this.elem,2*capacity);
            capacity*=2;//新的容量; 报错的原因是因为前面给capacity定义的final,不可更改，把final去掉就行了
        }
        for(int i=this.usedSize-1;i>=pos;i--){
            this.elem[i+1]=this.elem[i];
        }
        this.elem[pos]=data;
        this.usedSize++;
    }
    public void display(){//打印顺序表：把顺序表里面的所有元素都打印出来
        for(int i=0;i<this.usedSize;i++){
            System.out.print(this.elem[i]+" ");//打印i下标的值
        }
    }

    public boolean isEmpty(){//数组为空的情况
        return this.usedSize==0;//数组里面的有效数据的个数为0
    }
//判定是否包含某个元素
    public boolean contains(int toFind){ //判定是否包含某个元素：包含返回true
        if(isEmpty())
        return false ;//为空，找不到元素，返回false
        for(int i=0;i<this.usedSize;i++){
            if(this.elem[i]==toFind){//判断下标为i的数组的元素是否等于你要找的元素
                return true;//等于，找到了,返回true
            }
        }
        return false;//不等于，没找到，返回false
    }
//查找某个元素对应的位置
    public int search(int toFind){ //查找某个元素对应的位置:返回下标
        if(isEmpty())  return -1;//为空，找不到元素，返回-1
        for(int i=0;i<this.usedSize;i++){
            if(this.elem[i]==toFind){
                return i;//等于，找到了,返回i下标
            }
        }
        return -1;//找不到元素，返回-1
    }
//获取pos位置的元素       
    public int getPos(int pos){ //获取pos位置的元素：返回某一个下标的元素
        if(isEmpty()) {
            //return -1;//为空，找不到元素，返回-1
            throw new RuntimeException("顺序表是空的");//也可这样写，意思是手动抛出异常
        }
        if(pos<0 || pos>=this.usedSize){
            System.out.println("pos不合法");
            throw new RuntimeException("顺序表是空的");//pos不合法时，也抛出异常
        }
        return this.elem[pos];//不为空，返回pos下标的数据
    }
//给pos位置的元素设置为value
    public void setPos(int pos,int value){  //给pos位置的元素设置为value：把下标为几的元素改为其他值value
        if(pos<0 || pos>=this.usedSize){
            System.out.println("pos不合法");
            return;
        }
        if(isEmpty()){
            System.out.println("顺序表为空！");
            return ;
        }
        this.elem[pos]=value;
    }
//删除第一次出现的关键字key    
     public void remove(int toRemove){  //删除第一次出现的关键字key
        if(isEmpty()) return;//1.删的前提是不能让顺序表为空
        int index=search(toRemove);//定义index调用search函数，但是search函数里面判断的有找不到返回-1
        if(index==-1){//search函数里面判断的有找不到返回-1,所以这里也要判断一下是否找得到,然后返回
            System.out.println("没有你要删除的数字！");
            return;
        }
        //index如果你不是-1，就执行以下循环
        for(int i=index;i<this.usedSize-1;i++){//2.找到你想要删除的数据的下标，设为index
            this.elem[i]=this.elem[i+1];//3.后一个给前一个赋值;然后执行i++
        }
        this.usedSize--;//4.最后usedSize--
        
    }
//获取顺序表长度    
    public int size(){ 
        return this.usedSize;
    }
//清空顺序表    
    public void clear(){  //清空顺序表：相当于把每一个元素都置为0
        for(int i=0;i<this.usedSize;i++){
            this.elem[i]=0;
        }
        this.usedSize=0;//将usedSize也等于0，说明你当前顺序表的有效数据为0个，那再次将数据放进去的时候就可以从头开始放了。
    }
}    

删除数据的代码思路：

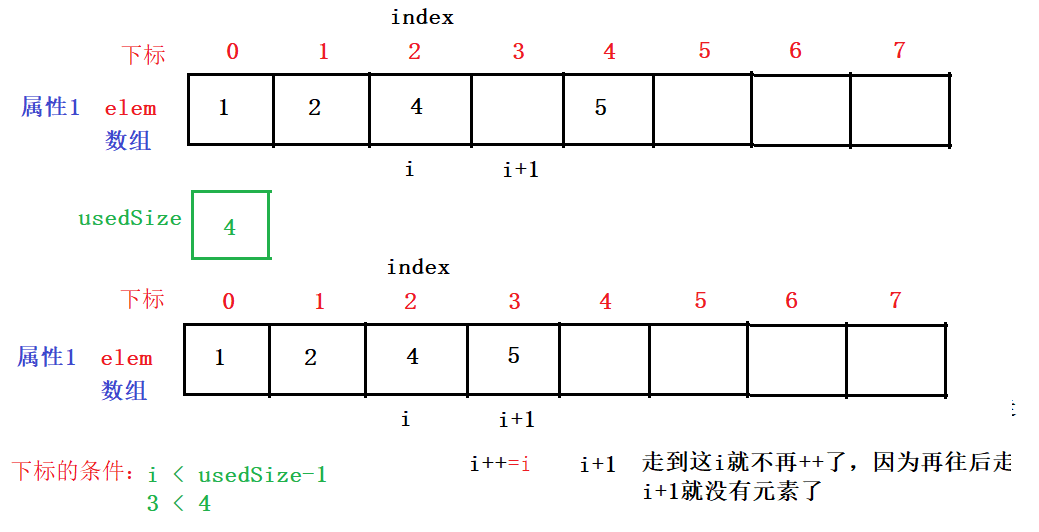
顺序表接口的测试代码

public class TestMyArrayList {
    public static void main(String[] args) {
        MyArrayList myArrayList=new MyArrayList();
        //测试add
        myArrayList.add(0,1);//表示在0下标放一个1
        myArrayList.add(1,2);//表示在1下标放一个2
        myArrayList.add(2,3);//表示在2下标放一个3
        myArrayList.add(3,4);//表示在3下标放一个4
        //测试remove
        myArrayList.remove(1);//remove没有返回值
//        myArrayList.remove(4);
        //测试clear
        myArrayList.clear();
        //测试打印
        myArrayList.display();

        //测试contains
        System.out.println(myArrayList.contains(5));
        System.out.println(myArrayList.contains(4));
        //测试search
        System.out.println(myArrayList.search(4));//查找4的下标
        System.out.println(myArrayList.search(5));//查找5的下标，不存在会返回 -1
        //测试getPos()
        System.out.println(myArrayList.getPos(1));//找下标为1的值
        System.out.println(myArrayList.getPos(10));//找下标为10的值，不合法会抛出异常
     }
}

测试打印结果

打印没有测试删除（remove）接口的结果如下：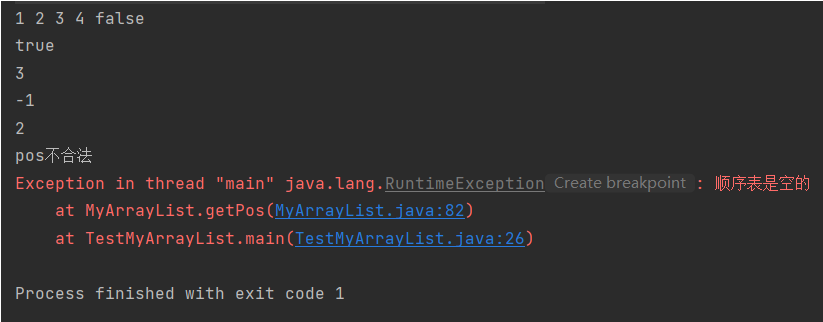

打印测试删除(remove)之后的结果如下：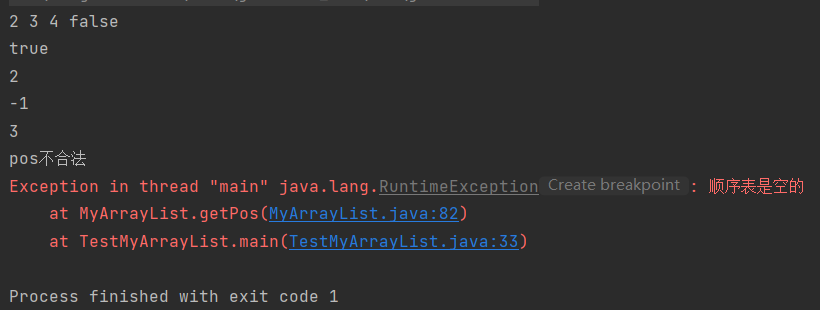

打印测试清空顺序表clear接口之后的结果：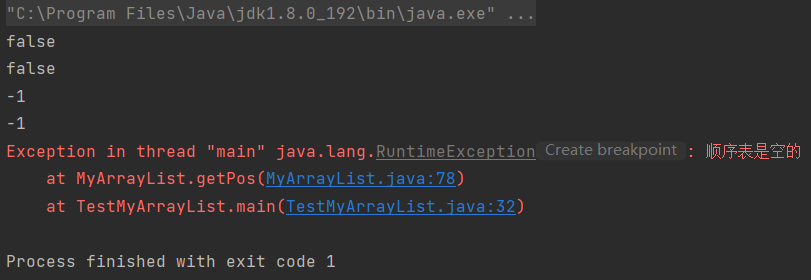

思考：顺序表增删查改的时间复杂度？

顺序表的优缺点其实就是数组的优缺点。

对顺序表来说：

1.如果要往顺序表里插入一个元素的时候，需要前后移动元素，最坏的情况就是往0下标放元素，需要把所有元素都移一遍.所以插入一个元素的时间复杂度的最坏情况是O(N)。

2.如果要删除一个元素，后面的元素需要往前移，最坏的情况就是删除第一个元素，此时需要把所有元素都往前移一遍，所以删除一个元素的时间复杂度的最坏情况是O(N)。

3.如果要查找一个元素：需要分两种情况

第一种：给定关键字：给定关键字需要一个一个找，所以它的时间复杂度是O(N);

第二种：给定下标:给定下标，直接确定元素的下标位置，找一次就能找到了，所以它的时间复杂度是O(1);

4.如果要修改一个元素，就需要给定下标才能改，所以它的时间复杂度是O(1);

所以，顺序表的优点：方便查找和修改；

如果经常涉及到查找和修改的问题，适合使用顺序表。

顺序表的缺点：1.不容易（不方便）插入和删除；

? 2.如果顺序表在满的情况需要插入数据，此时需要给顺序表扩容至2倍大，但如果只插入一个数据，那扩容之后的顺序表就只用了一个元素的空间，剩下的空间不用，就造成了浪费。

因此，如果经常涉及到插入和删除的问题，不适合使用顺序表，适合使用链表，因为链表的特点是随用随取，不会造成空间浪费；

总结：

1. 顺序表中间/头部的插入删除，时间复杂度为O(N)
2. 增容需要申请新空间，拷贝数据，释放旧空间。会有不小的消耗。
3. 增容一般是呈2倍的增长，势必会有一定的空间浪费。例如当前容量为100，满了以后增容到200，我们再继续插入了5个数据，后面没有数据插入了，那么就浪费了95个数据空间。

如何解决以上问题呢？下面给出了链表的结构来看看

三、链表

什么是链表？

链表：就是把数据以链式的形式串起来。

单链表的组织方式是由节点来组织数据（也就是由一个一个节点串起来的），每一个节点分为data域（数据域）和next域（下一个节点的引用）（也就是说每一个节点是由数值域和下一个节点的引用（地址）构成），分别存储当前节点的数据（如8,13等）和当前节点的下一个节点的地址（如0x325，0x673等），再用链表把它给串起来，最后一个节点没有下一个了，因此它的next域就是null。

通过画图来解决这个问题和上面这段话以及单链表和单链表的结构可能更好一点！

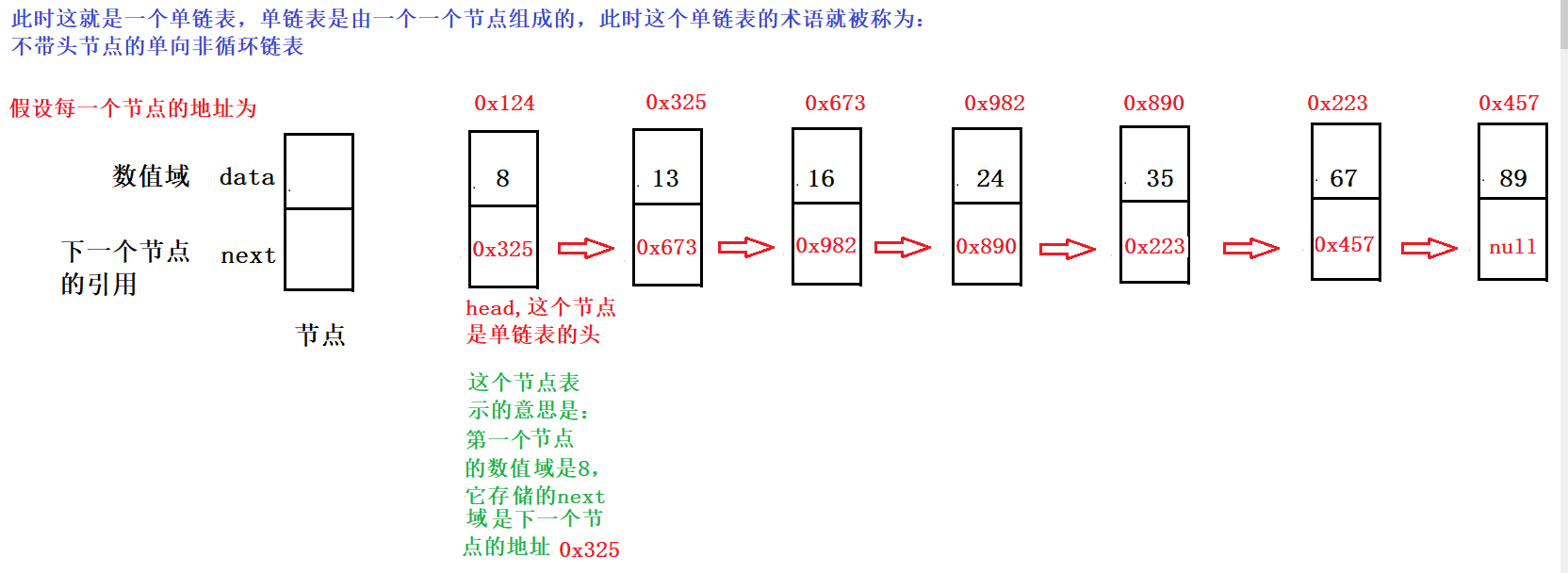
带头结点的单向非循环链表

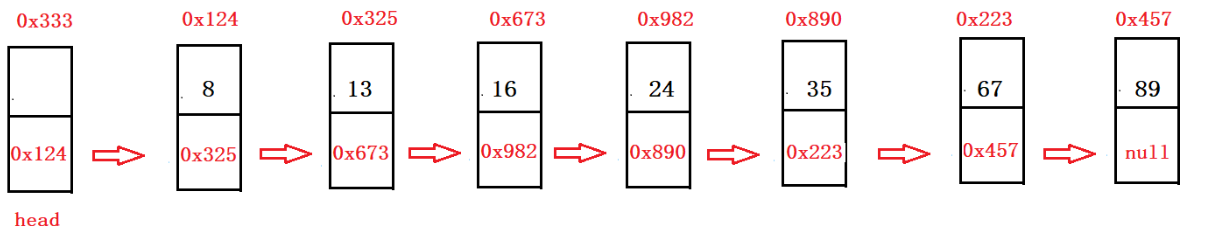
带头节点的单向循环链表

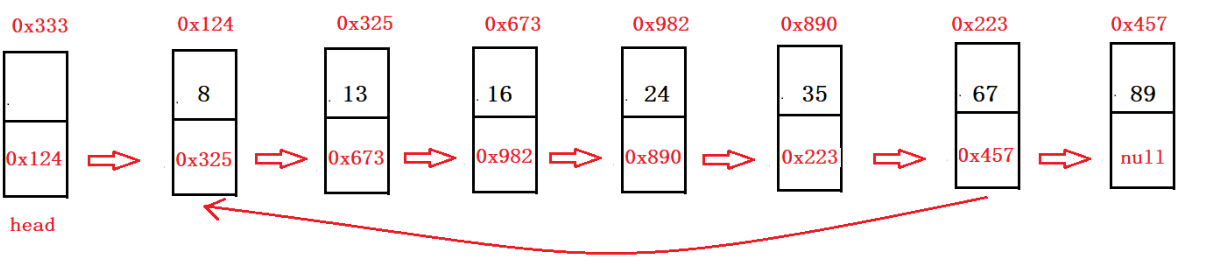
不带头节点的单向非循环链表和带头节点的单向非循环链表区别是什么呢？

• 不带头节点的单向非循环链表虽然在第一个节点的位置标注了它的头（head）,但那只是暂时的，在将来有可能当前节点就不是它的头了；
• 带头节点的单向非循环链表的data域是没有值的，不管怎样它就是单链表的头，并且不会发生改变；
• 因此他俩的唯一区别就是带头节点的单向非循环链表有一个专门来标识单链表的头的，不管在哪个地方放数据都不能把这个头部给换掉，相当于蛇头。不带头节点的单向非循环链表的头是不固定的，比如在当前节点的位置标注是它的头，如果把这个标注是它的头所存储的数据删掉，那它的头就移到了下一个节点的位置上，相当于没有头的 蛇，但对于带头节点的单向非循环链表的头，是不能删除的，只能删除它后面的节点。
• 带头节点的单向非循环链表：最后一个节点next域是null；
• 带头节点的单向循环链表:最后一个节点的next域不为空,才能循环，同时它的头不能发生改变，因此带头节点的单向循环链表比较简单。

我们重点研究不带头节点的单向非循环链表，因为带头的比较容易，不带头的研究会了，带头的就根本不是问题。

不带头节点的单向非循环列表

首先先把模型（类）写好:单链表由节点组成，所以要将节点抽象出来

链表是由一个一个节点组成的，每一个节点都有data域和next域，可以先把一个一个节点抽象出来，然后用类给它创建出来，有了类就可以产生这些对象了。

而每一个节点都是对象，它有两个属性，一个是data，一个是next；

对于属性data来说，可以是整型、字符型等，假设定义data为int类型；

next域保存的是节点地址，那它的类型就是节点类型，假设定义next的类型是Node类型

    class Node{//定义一个节点类型，Node就是节点，
        //每一个节点又有data域和next域，所以再定义两个属性
    public int data;//默认为0
    public Node next;//默认null,
    //类似于Person p1=new Person();
//Person()是一个对象，那p1也就是一个Person类型的
 
    //要产生节点，需要提供构造方法，然后实例化对象
    public Node(int data){//提供带有一个参数的构造方法，int data是Node里面的参数
        this.data=data;//实例化对象
        this.next=null;//写不写都可以，不写默认也是null
    }
}

• Node类型的next,为什么next是Node类型的？因为由next来保存下一节点的地址的话说明next也得是节点类型类似于Person p1=new Person();

如何产生一个节点？

如下图

△头插法addFirst方法

逻辑分析：使用头插法将生成的这个节点插入到单链表的头部，它的头就是head所指向的对象（这里先不考虑第一次插入）

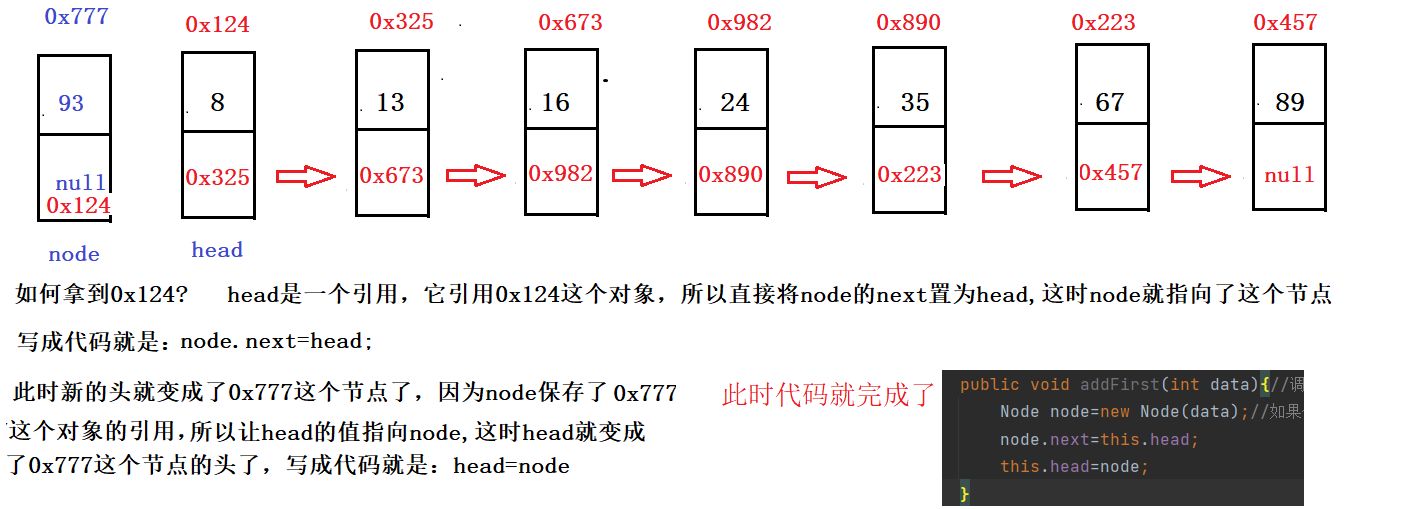
要想更加全面就要把第一次插入的情况也考虑进去，那么如果是第一次插入节点，逻辑是怎样的？代码又该怎样写呢？

逻辑分析如图：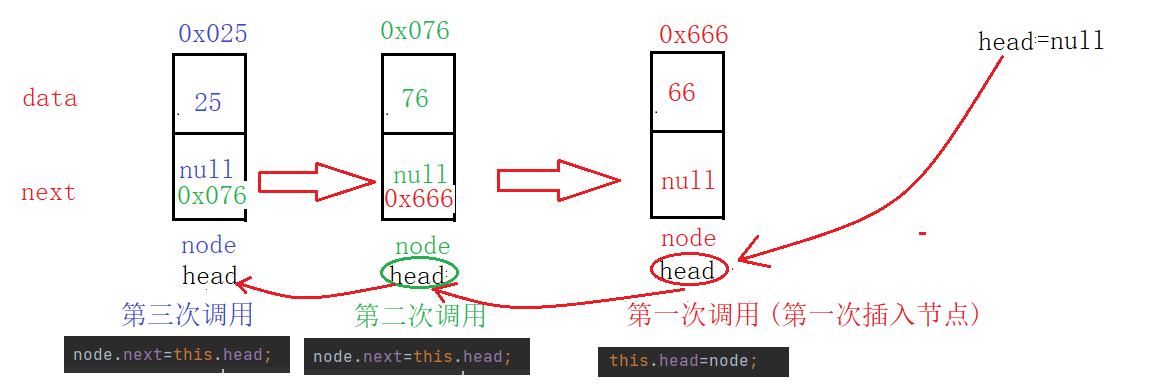

头插法的完整代码及解析如图：

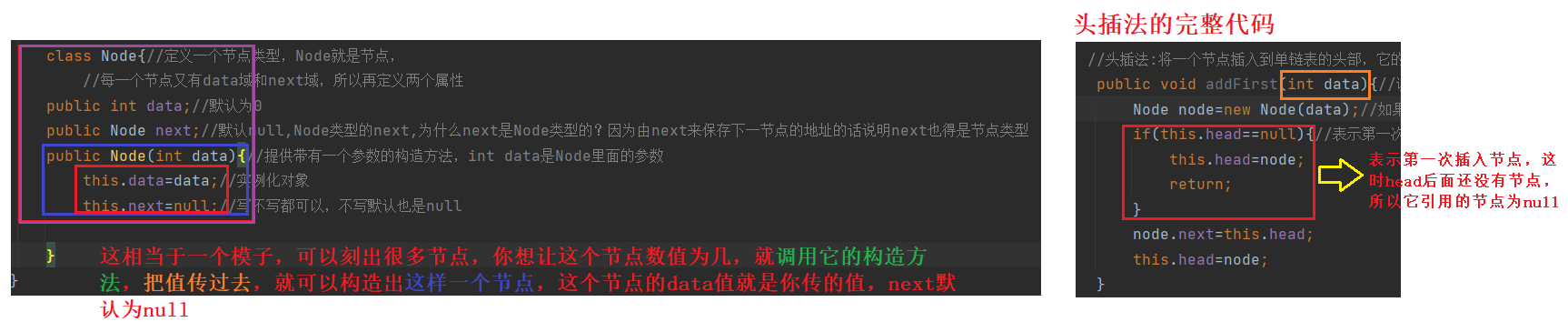
头插法addFirst方法代码示例

public class MyLinkedList {
        //为什么将head定义到MyLinkedList当中呢？因为head是它的成员属性，head标识的是整个单链表的头，而不是某个节点，所以要定义到MyLinkedList当中
       public Node head; //保存单链表的头节点的引用；head是一个引用，用来保存每个节点的地址，所以它也是Node类型，引用类型不初始化默认为null
    //这时需要使用方法将一个一个节点串起来，就成为单链表了

    //头插法:将一个节点插入到单链表的头部，它的头就是head所指向的对象
     public void addFirst(int data){//调用addFirst只能插入一个数据,因此就做到了随要随取，此时它的时间复杂度是O(1),因为没有循环
         Node node=new Node(data);//构造对象，如果传一个93，将数93传给带有一个参数的Node,对象new Node(data)就拿到了这个节点，这个节点的data域是这个数据93，而next域还为null，
         // 这个对象是由node引用的。画图
         if(this.head==null){//表示第一次插入节点，这时head后面还没有节点，所以它引用的节点为null
             this.head=node;
             return;
         }
         node.next=this.head;
         this.head=node;
     }

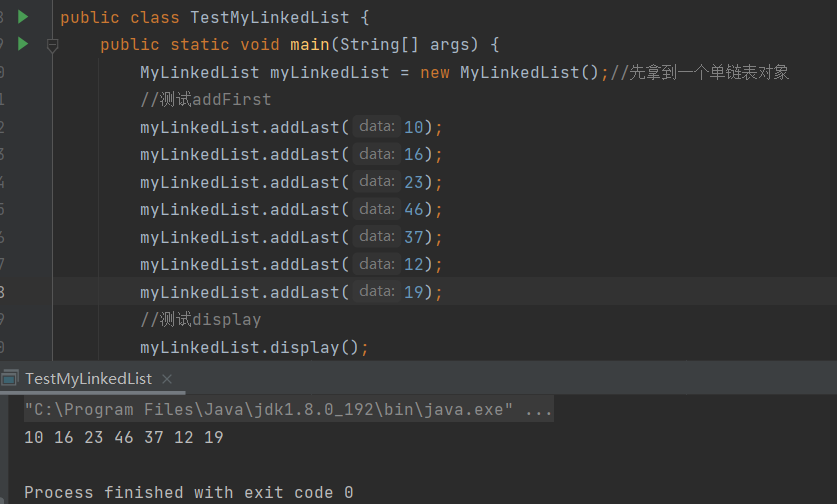
△尾插法addLast方法

尾插法：从单链表的尾部插入节点。

不考虑第一个节点为空的情况下的尾插法

逻辑分析如下：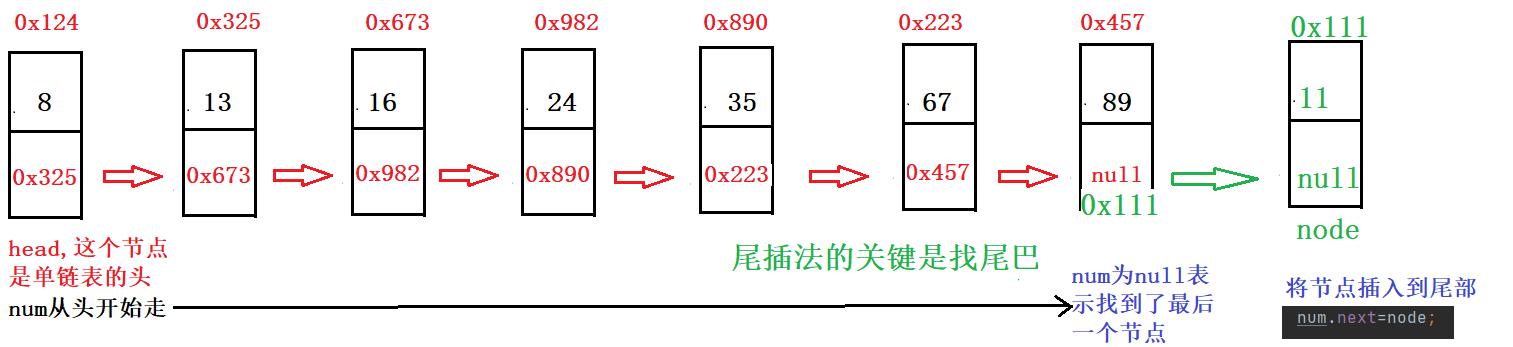

代码示例

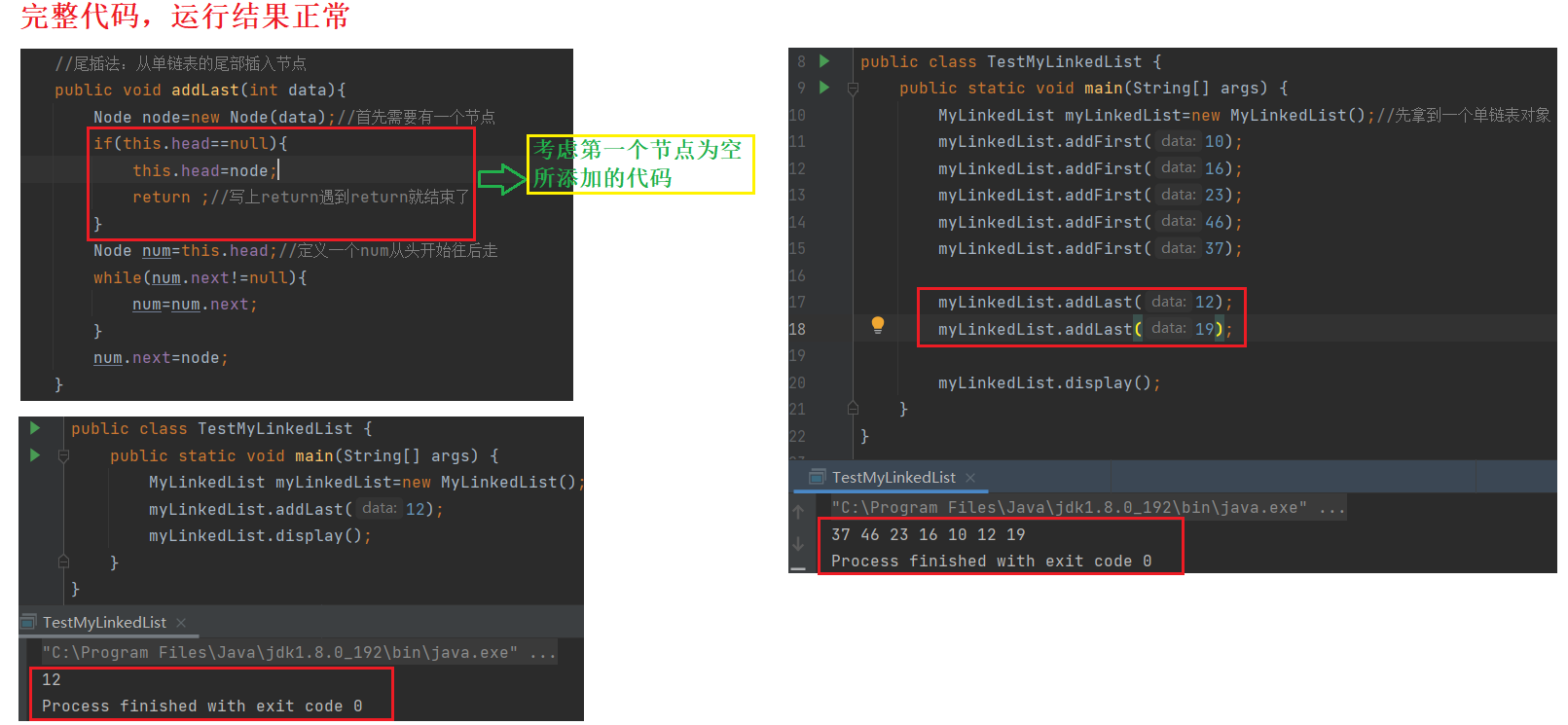
 //尾插法：从单链表的尾部插入节点
     public void addLast(int data){
         Node node=new Node(data);//首先需要有一个节点
         if(this.head==null){
             this.head=node;
             return ;//写上return遇到return就结束了
         }
         Node num=this.head;//定义一个num从头开始往后走
         while(num.next!=null){
             num=num.next;
         }
         num.next=node;
     }

考虑第一个节点为空的情况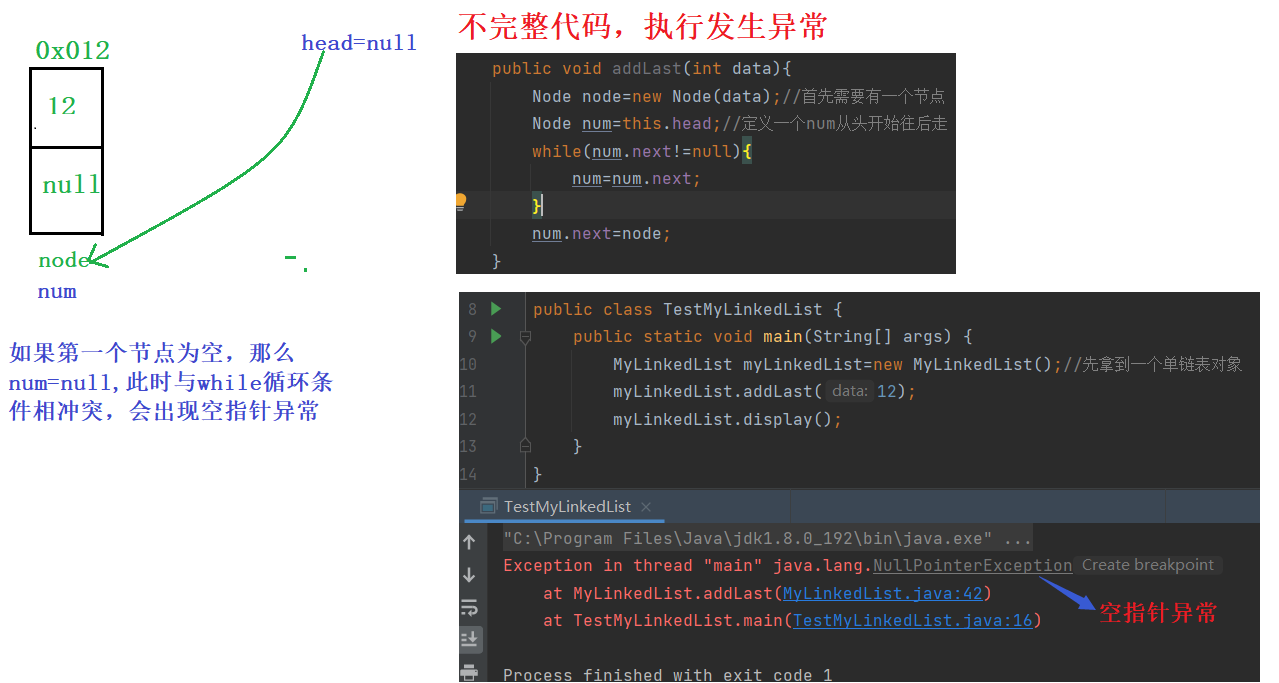

△任意位置插入addIndex方法

任意位置插入addIndex方法，第一个数据节点为0号下标

任意位置插入addIndex方法的逻辑，是addIndex有利于更好的利用头插法和尾插方法的使用。

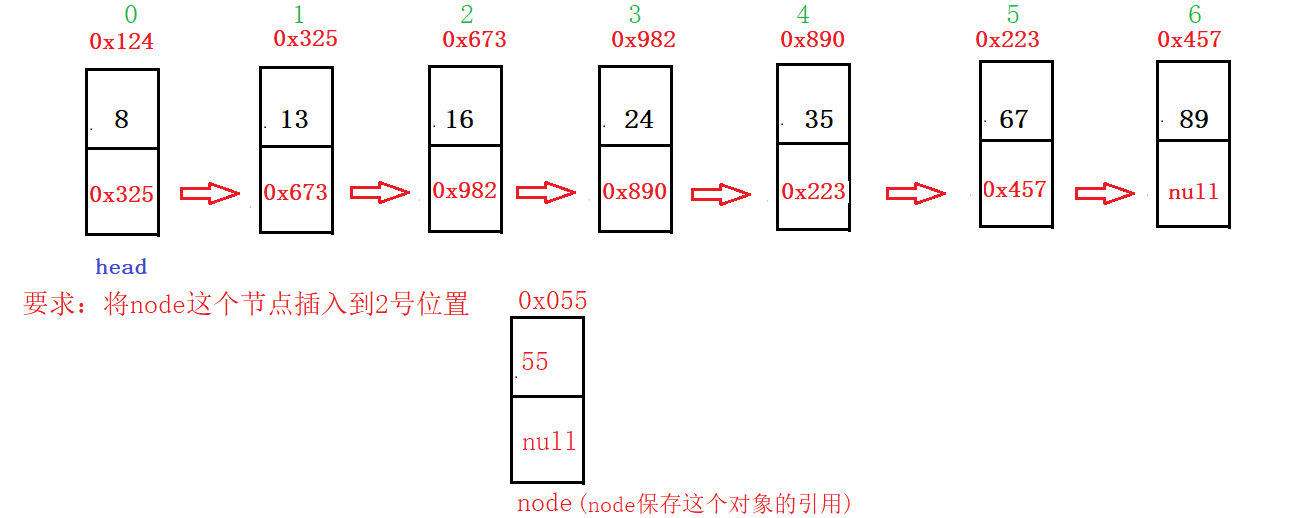
逻辑分析：想要往2号位置插入就要找到2号位置的前一节点即1号位置，因此就需要定义一个num先走到一号位置。

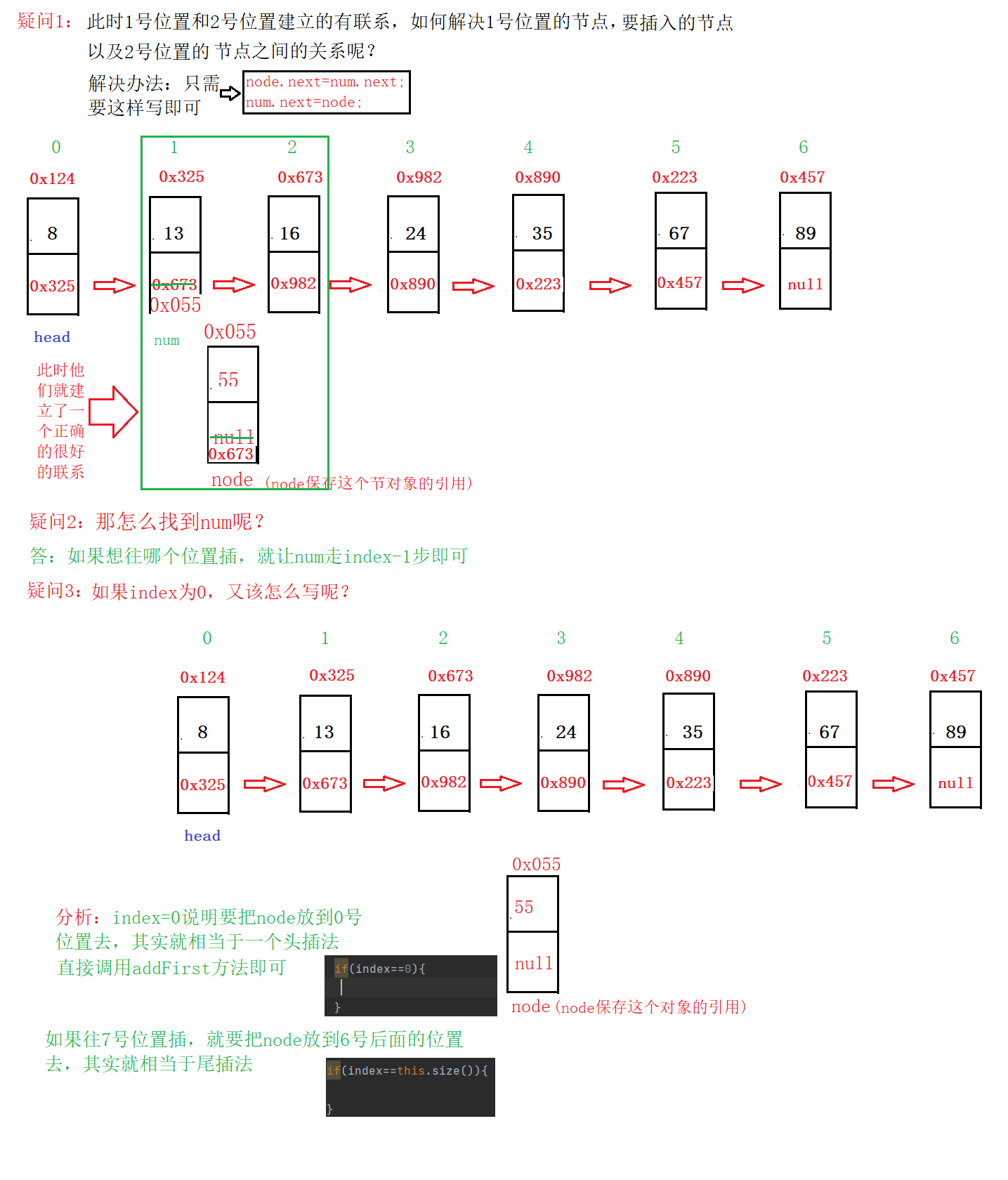
结合以上逻辑代码分析可以得出其步骤为：

1、先判断是否为头插或者尾插

2、定义一个num走index-1步，找到index位置的前一个节点的地址

3、找到之后，进行插入，插入的代码为

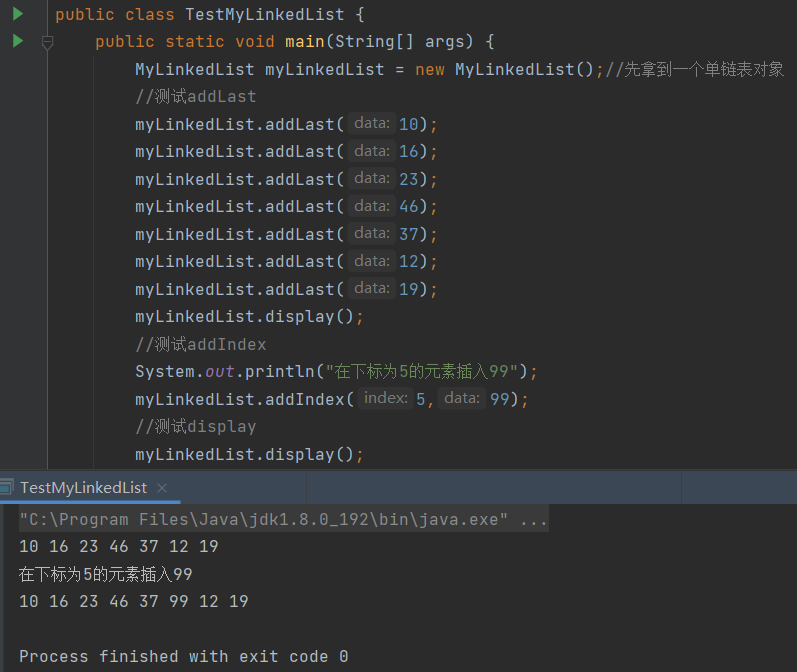
任意位置插入addIndex方法，代码示例

public void addIndex(int index,int data){//在index位置插入data数据
         if(index==0){//头插法
             addFirst(data);//调用头插法
             return;
         }
         if(index==this.size()){//尾插法
             addLast(data);//调用尾插法
             return;
         }
         Node node=new Node(data);//首先需要有一个节点
         //找index位置的前一个节点的地址
         Node num=searchIndex( index);//定义一个方法（函数），传入的值为index
         //进行插入
         node.next=num.next;
         num.next=node;
     }
     private Node searchIndex(int index){//Node是返回值，传入int index
         if(index<0||index>this.size()){   //对index进行合法性检查
             throw  new RuntimeException("index位置不合法！");
         }
         Node num=this.head;//index-1
         while(index-1!=0){
             num=num.next;
             index--;
         }
         return num;
     }

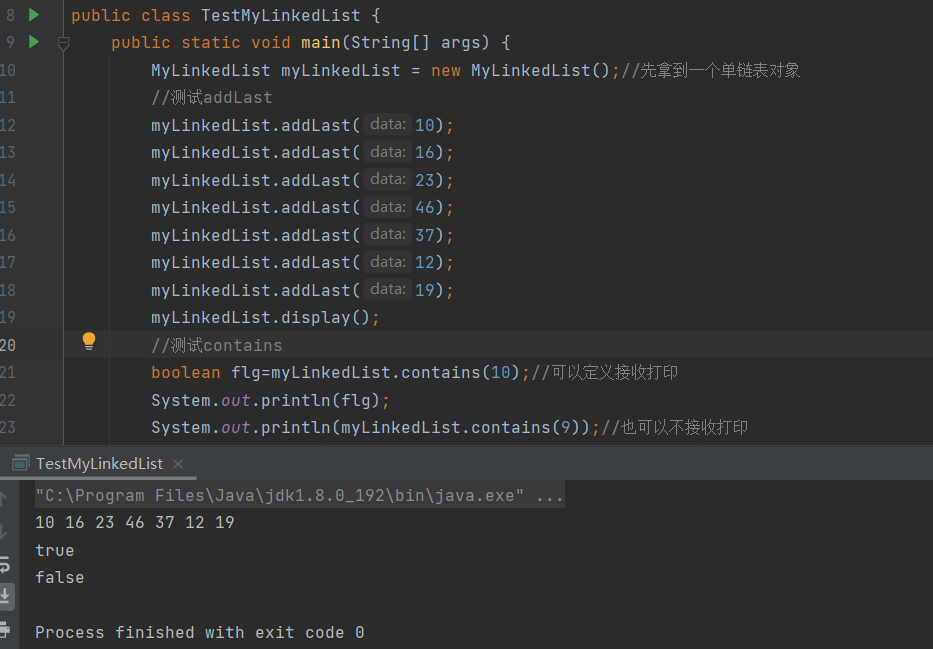
查找是否包含关键字key是否在单链表当中 contains方法

代码示例：

  public boolean contains(int key){
         Node num=this.head;
         while(num!=null){//当num为空的时候，结束循环，不为空的时候，遍历链表
             if(num.data==key){//判断数据域中的数据是否为你要找的那个数
                 return true;//是的话，返回true
             }
             num=num.next;//不是的话，继续遍历,知道遇到null
         }
         return false; //遍历完还没找到，返回false;
         // boolean类型不写返回值，会默认报错
     }

△删除第一次出现关键字为key的节点 remove方法

逻辑分析：我们可以倒着推。

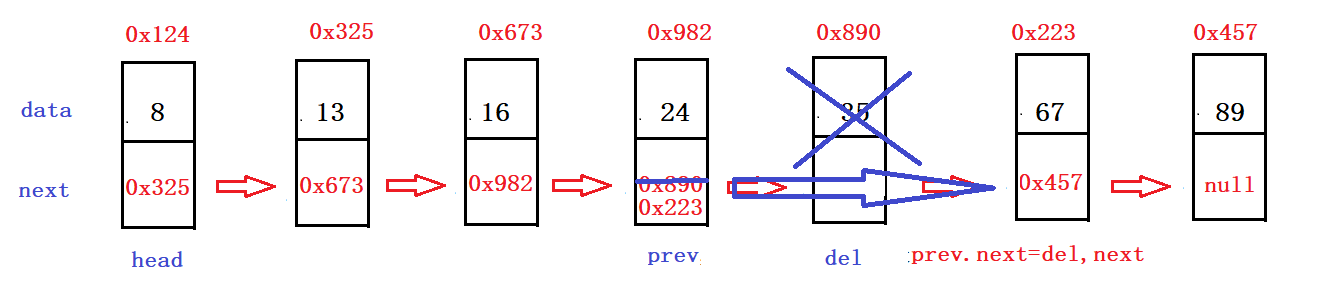
问题1：假设我们将35从这个列表中删除，需要考虑一些什么情况才能把它删除呢？

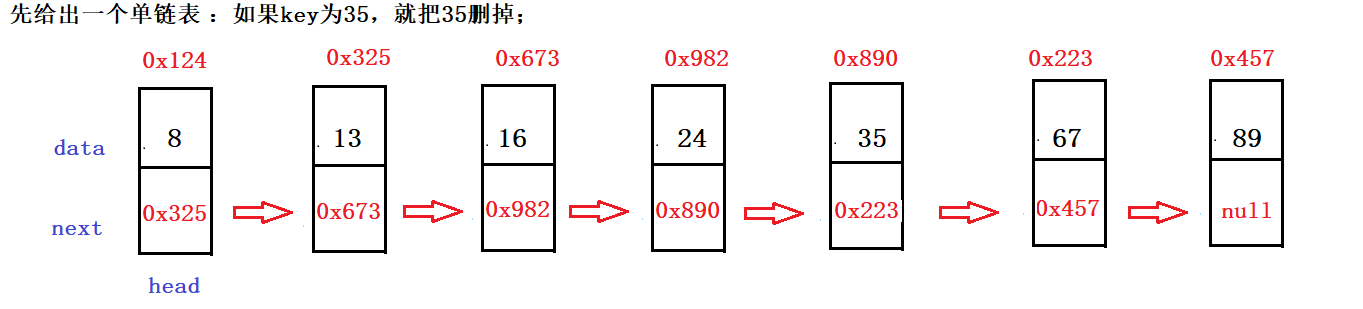
如果将保存0x890这个节点的地址变成保存0x223这个地址，那么就说明跳过了保存35这个数据的节点的地址0x890，删除这个节点也就意味着把35删除了

但是要想删除35这个节点，就必须先定义一个引用找到35前面的一个节点，然后将35前面的一个节点的next等于0x223就行了。

假设已经找到了这个节点，给它定义为prev,prev指向的就是你要删除的这个35这个节点的前驱,找到前驱之后，就可以将前驱的next值等于当前你要删除的这个节点的next值，将要删除的这个节点定义为del,那么此时写成代码就是prev.next=del,next，此时他就指向了0x223这个节点，而0x890这个节点就被删除了。

步骤总结：

首先你要知道你要删除的这个数据的节点del；

其次，你要找到你要删除的这个节点的前驱prev;

最后，让前驱的next值等于要删除的这个数据的节点next值。

问题2：那么如何知道他的前驱在哪呢？

如果想要删除35这个节点，需要定义一个引用prev从头开始走,那么如何判断prev指向了要删除的这个节点的前驱了呢？（先不考虑删除的节点是头结点）需要判断prev的下一个节点的数据，写成代码就是prev.next.data,

prev指向的是head即0x124这个节点，他的next是0x325这个值,prev.next代表prev的下一个节点，所以判断prev.next.data指向的值是否等于35即可，如果等于，就说明prev所指的就是35这个节点的前驱，此时就找到了要删除的这个节点的前驱prev,写成代码就是prev.next==35

前驱找到之后，del也就出现了，他等于当前prev的next值，写成代码就是Node del=prev.next.

根据前面的分析，使用prev.next=del,next，此时prev.next就指向了0x223这个节点。

代码如下：

//想要删除后面的，你要先找到你要删除的那个节点的前驱
         Node prev=searchPrev(key);//调用searchPrev来找当前key的前驱
         //调用完之后判断一下
         if(prev==null){
             System.out.println("表示没有这个节点");
             return;
         }
         //如果不等于空，开始删除
         Node del=prev.next;
         prev.next=del.next;
     }

步骤总结：

首先先让prev指向head,代码为prev=this.head;

其次判断prev.next.data指向的值是否等于你要删除的key,代码为if(prev.next.data== key),如果相等，就返回pretv，如果不相等，prev往后走，代码为：prev=prev.next，想要执行这个描述还需要一个循环，此时就需要考虑循环条件了，我们要找的是要删除节点的前驱，如果prev走到最后一个节点了，说明不存在prev.next.data==key，而prev的后面已经没有节点了，此时就会发生空指针异常,所以循环条件应该是while(prev.next!=null)。

如果整个循环都结束了还没有return出去，说明没有找到要删除的那个节点的前驱。那么就返回null，可以把这部分内容封装成一个函数。而这个函数的作用就是找关键字的前驱。

部分代码如下：

//封装函数
   private Node searchPrev(int key){//提供给remove的,所以写成私有的，Node设置节点类型，searchPrev找key的前驱
         Node prev=this.head;//prev从头开始走
         while(prev.next!=null){
             if(prev.next.data==key){
                 return prev;
             }else{
                 prev=prev.next;
             }
         }
       return null;//没找到前驱返回null
     } 

问题3：前面讨论的都是删除头结点后面的节点，如果想要删除第一个节点该怎么做呢？

假设要删除8这个节点，可以这样想，直接将head往后一挪就行了，此时8这个数据所在的节点就被删除了。

写成代码就是

//删除第一次出现关键字为key的节点：也就是给你一个数让你删除,这个数就是key
public void remove(int key){
         //删除头结点
         if(this.head==null){//先判断head是否为空
             return ;
         }
         if(this.head.data==key){//如果head不为null，判断head这个节点的数据是否为key,相等的话，说明你要删除的这个就是头结点，此时只需将head往后一步就好了。
             this.head=this.head.next;
             return ;
         }

完整代码如下：

//封装函数
     private Node searchPrev(int key){//提供给remove的,所以写成私有的，Node设置节点类型，searchPrev找key的前驱
         Node prev=this.head;//prev从头开始走
         while(prev.next!=null){
             if(prev.next.data==key){
                 return prev;
             }else{
                 prev=prev.next;
             }
         }
       return null;//没找到前驱返回null
     } 
//删除第一次出现关键字为key的节点：也就是给你一个数让你删除,这个数就是key
     public void remove(int key){
         //删除头结点
         if(this.head==null){//先判断head是否为空
             return ;
         }
         if(this.head.data==key){//如果head不为null，判断head这个节点的数据是否为key,相等的话，说明你要删除的这个就是头结点，此时只需将head往后一步就好了。
             this.head=this.head.next;
             return ;
         }
         //想要删除后面的，你要先找到你要删除的那个节点的前驱
         Node prev=searchPrev(key);//调用searchPrev来找当前key的前驱
         //调用完之后判断一下
         if(prev==null){
             System.out.println("表示没有这个节点");
             return;
         }
         //如果不等于空，开始删除
         Node del=prev.next;
         prev.next=del.next;
     }

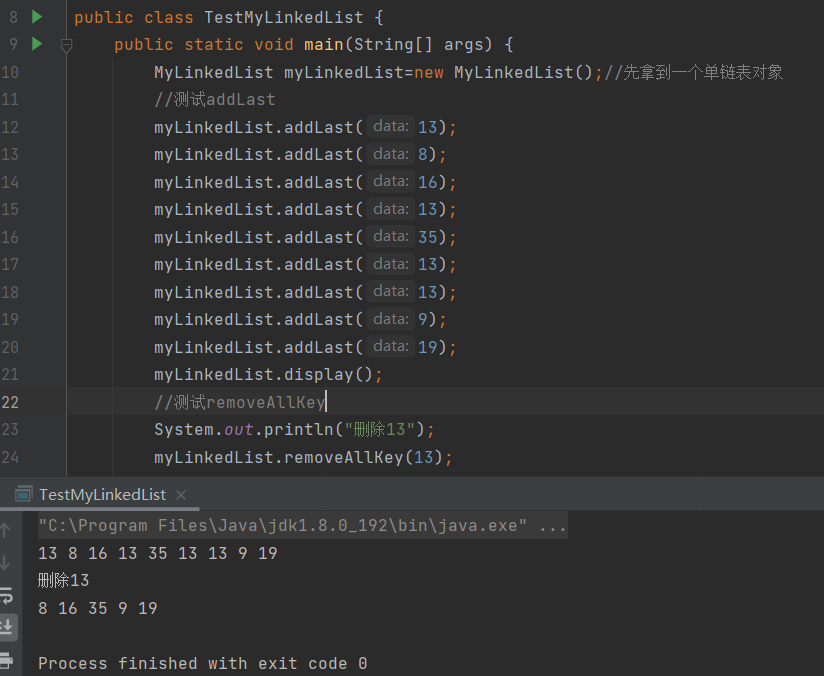
测试打印结果：

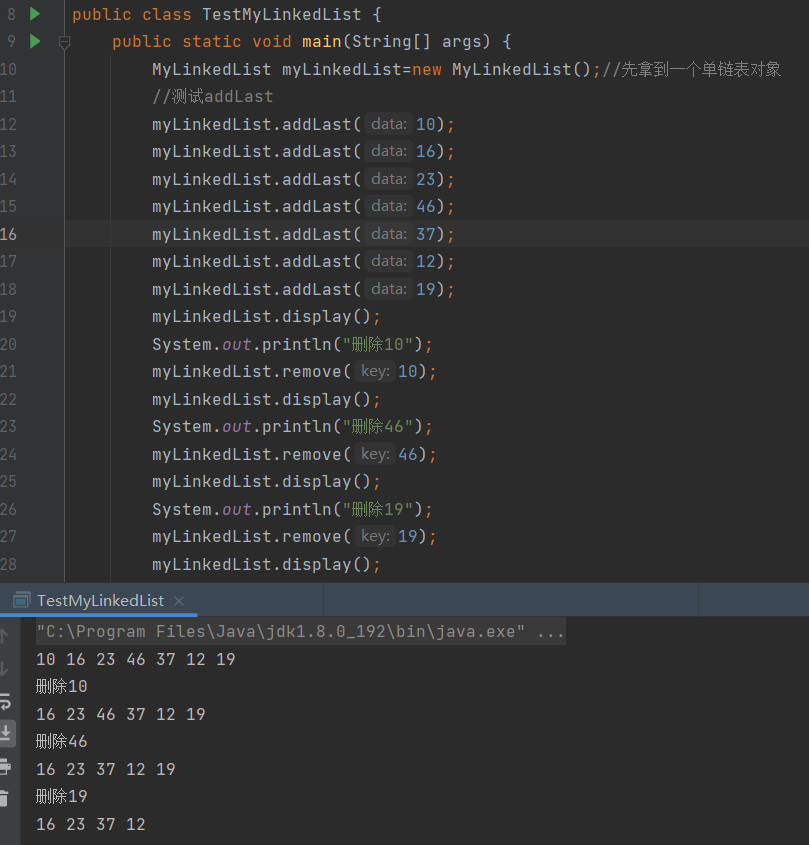
△删除所有值为key的节点removeAllKey方法

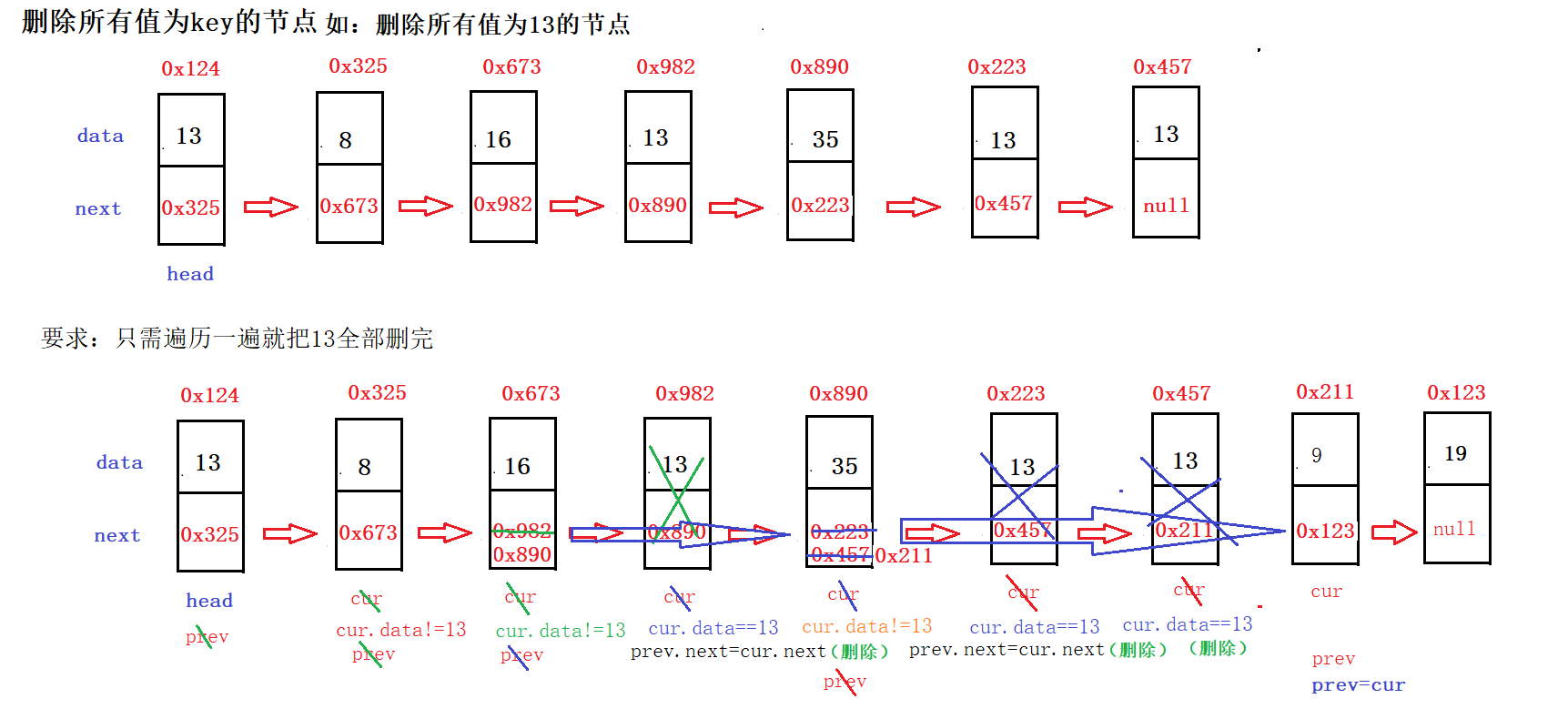
完整代码如下：

 public void removeAllKey(int key){
         Node prev=this.head;
         Node cur=prev.next;//代表要删除的节点
         //先不判断头是否为要删除的数据，只判断中间和尾部
         while(cur!=null){
             if(cur.data==key){//如果等于要删的值的话cur就继续走.prev不走
                 prev.next=cur.next;
                 cur=cur.next;
             }else{//如果不等于要删的值的话cur就继续走，prev走到cur这个地方，cur走到它的下一个节点
                 prev=cur;
                 cur=cur.next;
             }
         }
         //循环完成之后，就还剩头了，所以此时需要判断一下，如果第一个头结点就是要删除的数据该怎么办?
         if(this.head.data==key){
             this.head=this.head.next;
         }//此时就全部都删完了
        // 疑问：为什么一开始不删头呢？（单链表02   00:35:00讲解 ）
     }

得到单链表的长度 size方法

public int size(){
         int count=0;
         Node num=this.head;//定义一个num从头开始往后走
         while(num!=null){
             count++;
             num=num.next;
         }
         return count;//int类型也要写返回值，不然会报错
     }

打印单链表display方法

打印单链表:遍历链表（访问链表中的每一个元素即访问每一个节点中的data域）

public void display(){
         Node num=this.head;
         while(num!=null){//不等于null的时候说明有数据，可以打印，等于null时说明数据打印完了，
             System.out.print(num.data+" ");
             num=num.next;
         }
         System.out.println( );
     }

清除单链表clear方法

/**
     * clear是用来释放内存的
     * java当中的内存是由JVM自己回收的，但是有时候还是会有一些内存的泄露的
     * 内存泄漏指的是在程序运行过程中发生的内存泄露
     * JvM在回收对象的时候，当该对象在没有人引用他的时候，这个对象才会被回收
     */
     public void clear(){//通过clear函数将链表中的对象全部回收
         this.head=null;
     }

△链表接口的实现代码

public class MyLinkedList {
        //为什么将head定义到MyLinkedList当中呢？因为head是它的成员属性，head标识的是整个单链表的头，而不是某个节点，所以要定义到MyLinkedList当中
       public Node head; //保存单链表的头节点的引用；head是一个引用，用来保存每个节点的地址，所以它也是Node类型，引用类型不初始化默认为null
    //这时需要使用方法将一个一个节点串起来，就成为单链表了

//头插法:将一个节点插入到单链表的头部，它的头就是head所指向的对象
     public void addFirst(int data){//调用addFirst只能插入一个数据,因此就做到了随要随取，此时它的时间复杂度是O(1),因为没有循环
         Node node=new Node(data);//构造对象，如果传一个93，将数93传给带有一个参数的Node,对象new Node(data)就拿到了这个节点，这个节点的data域是这个数据93，而next域还为null，
         // 这个对象是由node引用的。画图
         if(this.head==null){//表示第一次插入节点，这时head后面还没有节点，所以它引用的节点为null
             this.head=node;
             return;
         }
         node.next=this.head;
         this.head=node;
     }    
//尾插法：从单链表的尾部插入节点
     public void addLast(int data){
         Node node=new Node(data);//首先需要有一个节点
         if(this.head==null){
             this.head=node;
             return ;//写上return遇到return就结束了
         }
         Node num=this.head;//定义一个num从头开始往后走
         while(num.next!=null){
             num=num.next;
         }
         num.next=node;
     }
//任意位置插入,第一个数据节点为0号下标
     public void addIndex(int index,int data){//在index位置插入data数据
         if(index==0){//头插法
             addFirst(data);//调用头插法
             return;
         }
         if(index==this.size()){//尾插法
             addLast(data);//调用尾插法
             return;
         }
         Node node=new Node(data);//首先需要有一个节点
         //找index位置的前一个节点的地址
         Node num=searchIndex( index);//定义一个方法（函数），传入的值为index
         //进行插入
         node.next=num.next;
         num.next=node;
     }
     private Node searchIndex(int index){//Node是返回值，传入int index
         if(index<0||index>this.size()){   //对index进行合法性检查
             throw  new RuntimeException("index位置不合法！");
         }
         Node num=this.head;//index-1
         while(index-1!=0){
             num=num.next;
             index--;
         }
         return num;
     }
//查找是否包含关键字key是否在单链表当中
     public boolean contains(int key){
         Node num=this.head;
         while(num!=null){//当num为空的时候，结束循环，不为空的时候，遍历链表
             if(num.data==key){//判断数据域中的数据是否为你要找的那个数
                 return true;//是的话，返回true
             }
             num=num.next;//不是的话，继续遍历,知道遇到null
         }
         return false; //遍历完还没找到，返回false;
         // boolean类型不写返回值，会默认报错
     }
    
//删除第一次出现关键字为key的节点
    //封装函数
     private Node searchPrev(int key){//提供给remove的,所以写成私有的，Node设置节点类型，searchPrev找key的前驱
         Node prev=this.head;//prev从头开始走
         while(prev.next!=null){
             if(prev.next.data==key){
                 return prev;
             }else{
                 prev=prev.next;
             }
         }
       return null;//没找到前驱返回null
     } 
//删除第一次出现关键字为key的节点：也就是给你一个数让你删除,这个数就是key
     public void remove(int key){
         //删除头结点
         if(this.head==null){//先判断head是否为空
             return ;
         }
         if(this.head.data==key){//如果head不为null，判断head这个节点的数据是否为key,相等的话，说明你要删除的这个就是头结点，此时只需将head往后一步就好了。
             this.head=this.head.next;
             return ;
         }
         //想要删除后面的，你要先找到你要删除的那个节点的前驱
         Node prev=searchPrev(key);//调用searchPrev来找当前key的前驱
         //调用完之后判断一下
         if(prev==null){
             System.out.println("表示没有这个节点");
             return;
         }
         //如果不等于空，开始删除
         Node del=prev.next;
         prev.next=del.next;
     }
//删除所有值为key的节点
public void removeAllKey(int key){
         Node prev=this.head;
         Node cur=prev.next;
         //先不判断头是否为要删除的数据，只判断中间和尾部
         while(cur!=null){
             if(cur.data==key){//如果等于要删的值的话cur就继续走.prev不走
                 prev.next=cur.next;
                 cur=cur.next;
             }else{//如果不等于要删的值的话cur就继续走，prev走到cur这个地方，cur走到它的下一个节点
                 prev=cur;
                 cur=cur.next;
             }
         }
         //循环完成之后，就还剩头了，所以此时需要判断一下，如果第一个头结点就是要删除的数据该怎么办?
         if(this.head.data==key){
             this.head=this.head.next;
         }//此时就全部都删完了
        // 疑问：为什么一开始不删头呢？（单链表02   00:35:00讲解 ）
     }
//得到单链表的长度
     public int size(){
         int count=0;
         Node num=this.head;//定义一个num从头开始往后走
         while(num!=null){
             count++;
             num=num.next;
         }
         return count;//int类型也要写返回值，不然会报错
     }
//打印单链表:遍历链表（访问链表中的每一个元素即访问每一个节点中的data域）
     public void display(){
         Node num=this.head;
         while(num!=null){//不等于null的时候说明有数据，可以打印，等于null时说明数据打印完了，
             System.out.print(num.data+" ");
             num=num.next;
         }
         System.out.println( );
     }
//清楚单链表
      public void clear(){//通过clear函数将链表中的对象全部回收
         this.head=null;
     }
     
}

△链表接口的测试代码

public class TestMyLinkedList {
    public static void main(String[] args) {
        MyLinkedList myLinkedList=new MyLinkedList();//先拿到一个单链表对象
        //测试addFirst
        myLinkedList.addFirst(10);
        myLinkedList.addFirst(16);
        myLinkedList.addFirst(23);
        myLinkedList.addFirst(46);
        myLinkedList.addFirst(37);
        //测试addLast
        myLinkedList.addLast(12);
        myLinkedList.addLast(19);
        myLinkedList.display();
        //测试addIndex
        myLinkedList.addIndex(5,99);
        //测试display
        myLinkedList.display();
        //测试contains
        boolean flg=myLinkedList.contains(10);//可以定义接收打印
        System.out.println(flg);
        System.out.println(myLinkedList.contains(9));//也可以不接收打印
        //测试size
        System.out.println(myLinkedList.size());
        //测试remove
        
        //打印数据链表
        myLinkedList.addLast(13);
        myLinkedList.addLast(8);
        myLinkedList.addLast(16);
        myLinkedList.addLast(13);
        myLinkedList.addLast(35);
        myLinkedList.addLast(13);
        myLinkedList.addLast(13);
        myLinkedList.addLast(9);
        myLinkedList.addLast(19);
        myLinkedList.display();
        //测试removeAllKey
        System.out.println("删除13");
        myLinkedList.removeAllKey(13);
        myLinkedList.display();
         
        //打印数据链表
        myLinkedList.addLast(10);
        myLinkedList.addLast(16);
        myLinkedList.addLast(23);
        myLinkedList.addLast(46);
        myLinkedList.addLast(37);
        myLinkedList.addLast(12);
        myLinkedList.addLast(19);
        myLinkedList.display();
        //测试remove
        System.out.println("删除10");
        myLinkedList.remove(10);
        myLinkedList.display();
        System.out.println("删除46");
        myLinkedList.remove(46);
        myLinkedList.display();
        System.out.println("删除19");
        myLinkedList.remove(19);
        myLinkedList.display();
        //清除单链表
        myLinkedList.addLast(10);
        myLinkedList.addLast(16);
        myLinkedList.addLast(23);
        myLinkedList.addLast(46);
        myLinkedList.addLast(37);
        myLinkedList.addLast(12);
        myLinkedList.addLast(19);
        myLinkedList.display();
        myLinkedList.clear();
    }
}

四、 顺序表和链表的区别和联系

顺序表

1、空间连续、支持随机访问。

2、中间或前面部分的插入删除时间复杂度为O(N)

3、增容的代价比较大。

链表：

1、以节点为单位存储，不支持随机访问

2、任意位置插入删除时间复杂度为O(1)

3、没有增容问题，插入一个开辟一个空间。