题目概述
如果希望循环队列中的元素都能得到利用,则可设置一个标志域tag,并以tag值为0或1来区分尾指针和头指针相同时的队列状态是“空”还是“满”,其数据结构如下:
typedef struct {
ElemType *elem;
int front;
int rear;
int tag;
int maxSize;
}CTagQueue;
1)写出此结构对应的队空判断条件表达式。
2)试编写与此结构对应的入队列算法 Status EnCQueue(CTagQueue &Q,ElemType x),插入元素为x,其返回值为 ERROR或OK.
题目解答
1)
(Q.tag==0)&&(Q.rear==Q.front)
2)
Status EnCQueue(CTagQueue &Q,QElemType x)
{
if((Q.tag==1)&&(Q.rear==Q.front))//队满
return ERROR;
Q.elem[Q.rear]=x;//新元素插入队尾
Q.rear=(Q.rear+1)%MAXQSIZE;//队尾指针加1
if(Q.tag==0) Q.tag=1;//标志改1,表示队列非空
return OK;
}
相关知识
背景问题
为了在C语言中描述方便起见,在此约定:初始化创建空队列时,令 front = rear = 0 , 每当插入新的队列尾元素时,尾指针 rear 增 1; 每当删除队列头元素时 , 头指针 front 增 1 。因此,在非空队列中,头指针始终指向队列头元素,而尾指针始终指向队列尾元素的下一个位置,如图所示。

假设当前队列分配的最大空间为 6, 则当队列处于上图(d) 所示的状态时不可再继续插入新的队尾元素,否则会出现溢出现象,即因数组越界而导致程序的非法操作错误。事实上,此时队列的实际可用空间并未占满,所以这种现象称为“假溢出”。这是由“队尾入队,队头出队”这种受限制的操作造成的。
循环队列
怎样解决这种“假溢出”问题呢?一个较巧妙的办法是将顺序队列变为一 个环状的空间,如图所示,称之为循环队列。
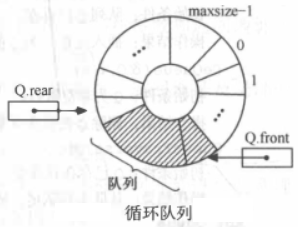
头、 尾指针以及队列元素之间的关系不变,只是在循环队列中,头、 尾指针“依环状增1”的操作可用“模”运算来实现。 通过取模,头指针和尾指针就可以在顺序表空间内以头尾衔接的方式“循环”移动。
在下图(a)中,队头元素是
J
5
J_5
J5?, 在元素
J
6
J_6
J6?入队之前,在Q.rear 的值为
5
5
5,当元素
J
6
J_6
J6?入队之后,通过“模”运算,
Q
.
r
e
a
r
=
(
Q
.
r
e
a
r
+
1
)
Q.rear = (Q.rear + 1)%6
Q.rear=(Q.rear+1), 得到 Q.rear 的值为0, 而不会出现前面普通队列“假溢出”状态。

在图(b)中,
J
7
、
J
8
、
J
9
、
J
10
J_7、J_8、J_9、J_{10}
J7?、J8?、J9?、J10? 相继入队, 则队列空间均被占满, 此时头、尾指针相同。
在图( c )中,
J
5
、
J
6
J_5、J_6
J5?、J6? 相继从图(a)所示的队列中出队, 使队列此时呈“空”的状态, 头、尾指针的值也是相同的。
由此可见,对于循环队列不能以头、尾指针的值是否相同来判别队列空间是“满”还是“空” 。在这种情况下, 如何区别队满还是队空呢?
通常有以下两种处理方法。
- 少用一个元素空间, 即队列空间大小为m时,有m-1个元素就认为是队满。这样判断队空的条件不变, 即当头、 尾指针的值相同时, 则认为队空;而当尾指针在循环意义上加1后是等于头指针, 则认为队满。因此, 在循环队列中队空和队满的条件是:
- 队空的条件: Q . f r o n t = Q . r e a r Q.front = Q.rear Q.front=Q.rear
- 队满的条件: ( Q . r e a r + 1 ) % M A X Q S I Z E = Q . f r o n t (Q.rear+ 1)\%MAXQSIZE = Q.front (Q.rear+1)%MAXQSIZE=Q.front
如图(d)所示, 当 J 7 、 J 8 、 J 9 J_7、J_8 、J_9 J7?、J8?、J9?进入图(a)所示的队列后, ( Q . r e a r + 1 ) % M A X Q S I Z E = Q . f r o n t (Q.rear+ 1)\%MAXQSIZE = Q.front (Q.rear+1)%MAXQSIZE=Q.front, 此时认为队满。
- 另设一个标志位 T a g Tag Tag以区别队列是“空”还是“满” 。具体描述参考本文题目解答
完整代码
#include<stdlib.h>
#include<stdio.h>
#define MAXQSIZE 100
#define OK 1
#define ERROR -1
#define OVERFLOW -1
typedef int QElemType;
typedef int Status;
typedef struct
{
QElemType *elem;
int front;
int rear;
int tag;
int maxSize;
}CTagQueue;
Status InitQueue(CTagQueue &Q)
{
Q.elem=(QElemType*)malloc(MAXQSIZE*sizeof(QElemType));
if(!Q.elem)
exit(OVERFLOW);//存储分配失败
Q.front=Q.rear=0;//头尾指针置为0
Q.tag=0;//标志初始化为0,队列为空
return OK;
}
int QueuenLength(CTagQueue Q)
{
return (Q.rear-Q.front+MAXQSIZE)%MAXQSIZE;//返回Q的元素个数,即队列长度
}
//入队
Status EnCQueue(CTagQueue &Q,QElemType x)
{
if((Q.tag==1)&&(Q.rear==Q.front))//队满
return ERROR;
Q.elem[Q.rear]=x;//新元素插入队尾
Q.rear=(Q.rear+1)%MAXQSIZE;//队尾指针加1
if(Q.tag==0) Q.tag=1;//标志改1,表示队列非空
return OK;
}
//出队
Status DeQueue(CTagQueue &Q,QElemType &e)
{
if((Q.tag==0)&&(Q.rear==Q.front))//队空
return ERROR;
e=Q.elem[Q.front];//保存队头元素
Q.front=(Q.front+1)%MAXQSIZE;//对头指针加1
if(Q.tag==1) Q.tag=0;//标志改0,表示队列非满
return OK;
}
//打印队列
void PrintQueue(CTagQueue Q)
{
while (((Q.rear+1)%MAXQSIZE==Q.front)||Q.front!=Q.rear)
{
printf("%d ",Q.elem[Q.front]);
Q.front++;
}
printf("\n");
}
int main()
{
CTagQueue Q;
QElemType m_e;
InitQueue(Q);
printf("入队顺序:\n");
for(int i=0;i<10;i++)
EnCQueue(Q,i);
for(int i=0;i<10;i++)
printf("%d ",Q.elem[i]);
printf("\n");
printf("出队顺序:\n");
for(int i=0;i<10;i++)
{
DeQueue(Q,m_e);
printf("%d ",m_e);
}
printf("\n");
system("pause");
return 0;
}
输出结果
参考文献
[1] 严蔚敏,吴伟民. 数据结构(C语言版). 北京: 清华大学出版社,2020
[2] 严蔚敏,李冬梅,吴伟民. 数据结构(C语言版)(第二版). 北京: 人民邮电出版社,2021
[3] 王道论坛. 2022数据结构考研复习指导. 北京:电子工业出版社,2021