本人能力有限,只是一个入门的学生,各位多多指教
题解只包括 (Cut The Wire)( Power Sum )(Command Sequence)
Cut The Wire
Problem Description In the country of Infinity , there is a strange
road. This road only has a starting point, but no end. Since this road is infinite, there are also countless street lights. The street lights are numbered from 1(the starting point) to infinity. The street lights are connected by wires under a strange law:For a street light x, if x is even, then x is connected with x2 by a wire; if x is odd, then x and 3x+1 is connected by a wire.Now Kris is standing in the middle of street light n and n+1, and he
is able to cut all wires passing by. That is, he will cut all wires
connecting street lights a and b satisfying a≤n and b>n.Now he wonders, how many wires he will cut. Please help him calculate.
Input
This problem contains multiple test cases.The first line contains an integer T(1≤T≤105) indicating the number of test cases.
The next T lines each contains one integer n(1≤n≤109).
Output
For each test case, output one line of one integer indicating
the answer.Sample Input
2
12
60
Sample Output
10
50
此题需要明白题意,了解题目意思,意思如下:假设有电线杆数从一开始下标,从中间有一个数n 和 n+1电线杆之间 有许多电线,问你能剪短多少根电线,电线连接方式 两种 ① 如果第 x 根电线是偶数 那么他和第 x/2 根电线连接 ② 如果第 x 根电线是奇数 那么他和第 3*x+1 根电线连接 (电线的跨度必须是大于n 小于 n+1)
如下图表示:
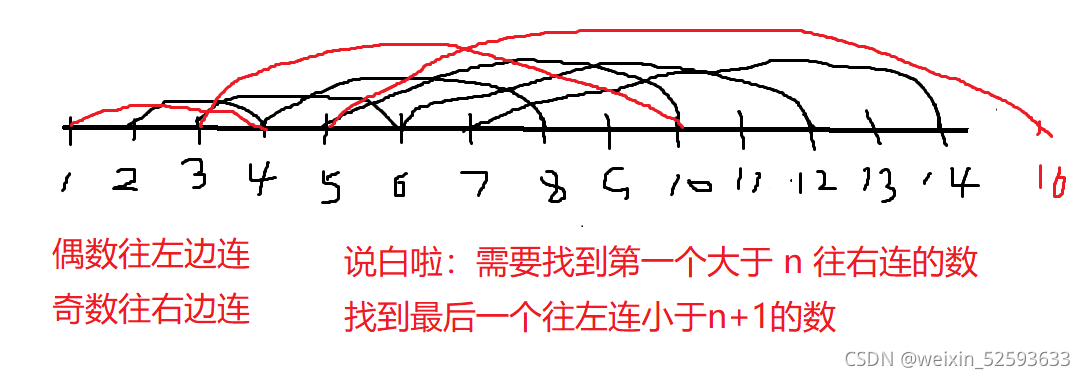
左边:用 n=3x+1 得 x= (n-1)/3 ; n-(n-1)/3 是 n-3 到 n 的个数
加一不加一是奇偶的差别 除2 是区间奇偶个数
右边:(2n - n)/2 =n/2 加一不加一是奇偶的差别

#include<iostream>
using namespace std;
int main()
{
int T;
cin >>T;
while(T--)
{
int n;
cin >>n;
int res=0;
//左边的数连线大于 n
if(n%2==0)
res+=(n-n/3)/2;
else
res+=((n-(n-1)/3)+1)/2;
//右边的数连线小于 n+1
if(n%2==0)
res+=n/2;
else
res+=(n/2)+1;
cout <<res <<endl;
}
return 0;
}
Power Sum
Problem Description Given a positive number n, Kris needs to find a positive number k and an array {ai}(ai∈{?1,1}) of length k (1≤k≤n+2)
such that:
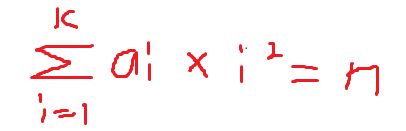
This is too hard for Kris so you have to help him.
Input
The input contains multiple test cases.The first line contains an integer T(1≤T≤100) indicating the number of test cases.
Each of the next T lines contains one integer n(1≤n≤106).
It’s guaranteed that ∑n≤3?107.
Output
The output should contain 2T lines.
For each test case, output two lines.The first line contains one integer, k.
The second line contains a 01-string of length k representing the array, with 0 in the ith position denoting ai=?1 and 1 denoting ai=1.If there are multiple answers, print any.
Sample Input
2
1
5
Sample Output
1
1
2
11
题目理解:
本来这个题用递归就行啦,但是 用递归需要自己手写栈 要不然就爆啦
仔细一想这这题应该是又能统一起来找点规律,每一项都是正负这种形式,
是不是可以有确定项的加减,总结规律如下(a1+a4) - (a2+a3)=4
所以就要搞 一下 n%1==0 1 2 3 这四种情况,构造出来,1 2 3
构造如下:
① 1=1 ‘1’
② -1-4-9+16 =2 “0001”
③ -1+4 =3 ‘‘01’’
#include<iostream>
using namespace std;
int main()
{
int T;
cin >>T;
while(T--)
{
int n;
cin >>n;
int k;
string s;
if(n%4==1)
{
k=1+(n/4)*4;
s+='1';
for(int i=1;i<=n/4;i++) s+="1001";
}
else if(n%4==2)
{
k=4+(n/4)*4;
s+="0001";
for(int i=1;i<=n/4;i++) s+="1001";
}
else if(n%4==3)
{
k=2+(n/4)*4;
s+="01";
for(int i=1;i<=n/4;i++) s+="1001";
}
else
{
k=n;
for(int i=1;i<=n/4;i++) s+="1001";
}
cout <<k <<endl<<s<<endl;
}
return 0;
}
Command Sequence
Problem Description
There is a robot that can move by receiving a sequence of commands.
There are four types of command in the command sequence:
U: robot moves one unit up. D: robot moves one unit down. L: robot moves one unit left. R: robot moves one unit right.Now, given a command sequence of length n. You need to find out how many substrings of the command sequence satisfy that if the robot execute the substring command, it can return to the starting position.
A substring is a contiguous sequence of characters within a string.
For instance, “the best of” is a substring of “It was the best of times”. For example, “Itwastimes” is a subsequence of “It was the best of times”, but not a substring.Input
This problem contains multiple test cases.
The first line contains an integer t (1≤t≤20) indicating the number of
test cases.For each test case, the first line contains one integer n (2≤n≤105).
The second line contains a UDLR string of length n.
Output
For each test case, output one line one integer indicating the answer.
Sample Input
1
6
URLLDRSample Output
2
题目解释:
就是一个图题,按照以往的经验,是用dfs ,最短路都不是 所以这可能还是需要总结考虑如果是想回到起点
当然想到的就是相互抵消,那如果是子字符串呢?当然就是枚举前缀和,但是提交就是超时
当然如果想到是用开数组那就更不行啦,因为数组一开必然就会超时啦,但是转念一想,用map的一维数组记录每个点的次数,pair存一下点的坐标,无非就是看一下该点是否出现不止一次,
解释样例:
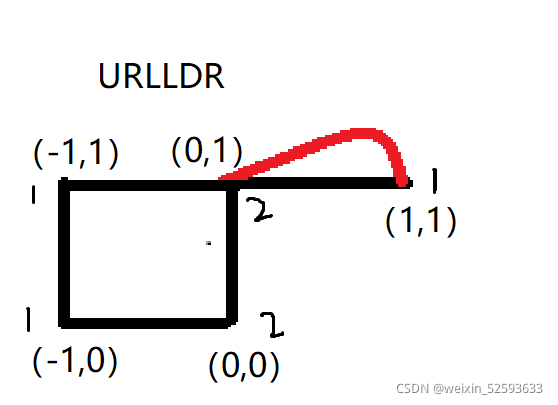
样例中有两个点出现了两次,说明有两个点可以回到原点,其他点都只走了一回,不可能回到原点,
如果一个点出现了三次 比如 UDDURL
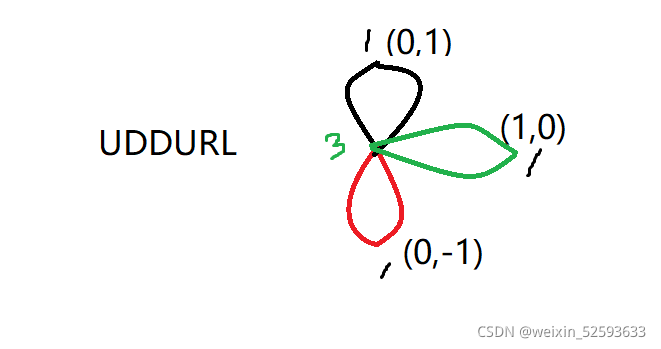
他可能的序列有六个
UD
UDDU
UDDURL
DU
DURL
RL
6 = 1 + 2 + 3
#include<iostream>
#include<map>
using namespace std;
typedef long long ll;
typedef pair<int,int>PII;
int main()
{
int T;
cin>>T;
while(T--)
{
map<PII,int>mp; //每次重新定义一个map数组
int n;
string s;
cin>>n >>s;
mp[{0,0}]++; //按起始点为1 开始
ll res=0,p=0,q=0;
for(int i=0;i<s.size();i++)
{
if(s[i]=='U') p++;
else if(s[i]=='R') q++;
else if(s[i]=='L') q--;
else p--;
res+=mp[{p,q}]; //这里先加上这个点的个数
mp[{p,q}]++; //然后这个点在 加一
}
cout <<res <<endl;
}
return 0;
}