ST表简介
ST表(Sparse Table,稀疏表)是一种简单的数据结构,主要用来解决RMQ(Range Maximum/Minimum Query,区间最大/最小值查询)问题。它主要应用倍增的思想,可以实现 O(nlogn) 预处理、O(1) 查询。
所谓RMQ问题,以最大值为例,是假如有一个数列 A ,给你一个区间 [l , r] ,要求 max(A_i),l<=i<=r。
ST表使用一个二维数组f,对于范围内的所有 f[a][b],先算出并存储 max(A_i),a<=i<a+2^b(本文中的区间都是离散意义下的,只包含整数,所以此区间也可以写成 a<=i<=a+2^b-1 ),这称为预处理。查询时,再利用这些子区间算出待求区间的最大值。
动态规划的预处理(以2为倍数增加长度)
为了减少时间复杂度,可以用动态规划的方法进行预处理:
int f[MAXN][21]; // 第二维的大小根据数据范围决定,不小于log(MAXN),故遍历的时间复杂度是O(NlogN)
for (int i = 1; i <= n; ++i)
f[i][0] = read(); // 读入数据
//这段转移过程的原理在于,先算出长度为2的区间max,再根据2的次数幂进一步扩散,而由于区间长度总是上一次的两倍,所以可以直接两个上一次的答案推出这次的答案,故得图下的状态转移过程
for (int i = 1; i <= 20; ++i)
for (int j = 1; j + (1 << i) - 1 <= n; ++j)
f[j][i] = max(f[j][i - 1], f[j + (1 << (i - 1))][i - 1]);
这个地方就是ST表的妙处之一,用第二维表示2的指数,也是一个很妙的思想了,这样大大节约了存储空间。
原理如下图所示:
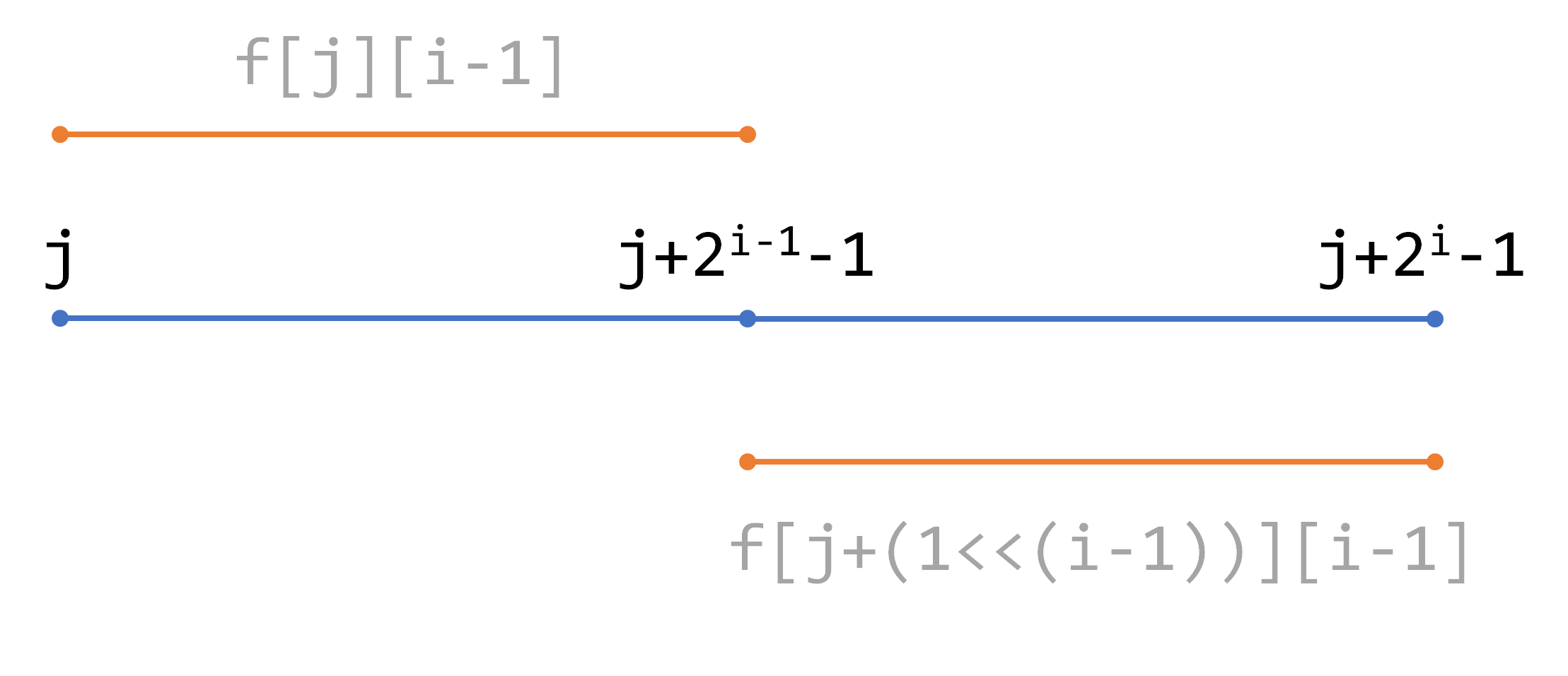
注意1<<i 相当于 2^i 。
区间查询的方法
比如我们要查询 [l , r] 的最大值,我们需要找到两个 [l , r] 的子区间,他们的并集恰好是 [l , r] (不需要严格不相交,只需要两者把整个区间包含)。具体地说,我们要找的是一个整数 s ,两个子区间分别为 [l , l+2^s-1] 和 [r-2^s+1 , r] 。
(如下图)

所以我们希望前一个子区间的右端点尽可能接近r。当 l+2^s-1=r 时,得到表达式 s=log2(r-l+1) ,由于 s 需要为整数,所以这个结果需要向下取整。
每次计算log太花时间了,我们可以对log也进行一次递推的预处理:
for (int i = 2; i <= n; ++i)
Log2[i] = Log2[i / 2] + 1;
当然这个过程也可以用 std::__lg() 这个函数来代替,它也是求log2的向下取整的值,同样也是O(1)复杂度。
- 有了以上过程的分析,查询过程的代码就出来了:
for (int i = 0; i < m; ++i)
{
int l = read(), r = read();
int s = Log2[r - l + 1];
printf("%d\n", max(f[l][s], f[r - (1 << s) + 1][s]));
}
其实ST表不仅能处理最大值/最小值,凡是符合结合律且可重复贡献的信息查询都可以使用ST表高效进行。什么叫可重复贡献呢?设有一个二元运算 f(x,y) ,满足 f(a,a) = a 则 f 是可重复贡献的。显然最大值、最小值、最大公因数、最小公倍数、按位或、按位与都符合这个条件。可重复贡献的意义在于,可以对两个交集不为空的区间进行信息合并。
例题一:ST表模板题
解题代码:
#include <bits/stdc++.h>
using namespace std;
#define MaxN 100002
int f[MaxN][22];
int N, M;
inline int read() {
int x = 0, f = 1;
char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-')
f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + ch - 48;
ch = getchar();
}
return x * f;
}
int main() {
scanf("%d%d", &N, &M);
for (int i = 1; i <= N; i++) {
f[i][0] = read();
}
//更新f数组
for (int i = 1; i < 22; i++) {
for (int j = 1; j + (1 << i) - 1 <= N; j++) {
f[j][i] = max(f[j][i - 1], f[j + (1 << (i - 1))][i - 1]);
}
}
//打印答案
for (int i = 0; i < M; i++) {
int l = read();
int r = read();
int s = __lg(r - l + 1);
printf("%d\n", max(f[l][s], f[r - (1 << s) + 1][s]));
}
return 0;
}
例题二:ST表变式例题
题目背景
每天,农夫 John 的N(1 <= N <= 50,000)头牛总是按同一序列排队. 有一天, John 决定让一些牛们玩一场飞盘比赛. 他准备找一群在对列中为置连续的牛来进行比赛. 但是为了避免水平悬殊,牛的身高不应该相差太大. John 准备了Q (1 <= Q <= 200,000) 个可能的牛的选择和所有牛的身高 (1 <= 身高 <= 1,000,000). 他想知道每一组里面最高和最低的牛的身高差别.
输入格式
第1行:N,Q
第2到N+1行:每头牛的身高
第N+2到N+Q+1行:两个整数A和B,表示从A到B的所有牛。(1<=A<=B<=N)
输出格式
输出每行一个数,为最大数与最小数的差
题目链接:
(洛谷P2880 [USACO07JAN]平衡的阵容Balanced Lineup)
#include <bits/stdc++.h>
#define MAXN 50005
using namespace std;
int read()
{
int ans = 0;
char c = getchar();
while (!isdigit(c))
c = getchar();
while (isdigit(c))
{
ans = ans * 10 + c - '0';
c = getchar();
}
return ans;
}
int Log2[MAXN], Min[MAXN][17], Max[MAXN][17];
int main()
{
int n = read(), m = read();
for (int i = 1; i <= n; ++i)
{
int x = read();
Min[i][0] = x;
Max[i][0] = x;
}
//这里可以换成是std::__lg(),就没必要求这个Log2了
for (int i = 2; i <= n; ++i)
Log2[i] = Log2[i / 2] + 1;
for (int i = 1; i <= 16; ++i)
for (int j = 1; j + (1 << i) - 1 <= n; ++j)
{//同时求出最大值区间和最小值区间
Min[j][i] = min(Min[j][i - 1], Min[j + (1 << (i - 1))][i - 1]);
Max[j][i] = max(Max[j][i - 1], Max[j + (1 << (i - 1))][i - 1]);
}
for (int i = 0; i < m; ++i)
{//求出这个区间的最大值和最小值便可得到最大差值
int l = read(), r = read();
int s = Log2[r - l + 1];
int ma = max(Max[l][s], Max[r - (1 << s) + 1][s]);
int mi = min(Min[l][s], Min[r - (1 << s) + 1][s]);
printf("%d\n", ma - mi);
}
return 0;
}
例题三:ST表的思想解决多数求gcd
题目背景
“叮铃铃铃”,随着高考最后一科结考铃声的敲响,三年青春时光顿时凝固于此刻。毕业的欣喜怎敌那离别的不舍,憧憬着未来仍毋忘逝去的歌。1000多个日夜的欢笑和泪水,全凝聚在毕业晚会上,相信,这一定是一生最难忘的时刻!
题目描述
彩排了一次,老师不太满意。当然啦,取每位同学的号数来找最大公约数显然不太合理。于是老师给每位同学评了一个能力值。于是现在问题变为,从n个学生中挑出k个人使得他们的默契程度(即能力值的最大公约数)最大。但因为节目太多了,而且每个节目需要的人数又不知道。老师想要知道所有情况下能达到的最大默契程度是多少。这下子更麻烦了,还是交给你吧~
PS:一个数的最大公约数即本身。
输入格式
第一行一个正整数n。
第二行为n个空格隔开的正整数,表示每个学生的能力值。
输出格式
总共n行,第i行为k=i情况下的最大默契程度。
题目链接:
解题分析:
我们想到,k个数的公约数含义就是这k个数均含有某个因数,如果我们把所有数的因数全部求出来,发现有k个数均含有某个因数,那么这个数必然是这k个数的公约数。其中找出最大的就是它们的最大公约数。
求出出现任取k个数的最大公约数后,我们发现有些数如果没有对应的次数,则一直是0未更新的状态,实际上我们只要约数出现次数大于了k次,都可以被 k 次当做结果来利用,所以还会出现一个状态转移过程:
ans[k]=max(ans[k],ans[k+1])。意思就是选取大于k次的最大因子,实际上是可以为k次所用。
解题代码:
#include<cstdio>
#include<iostream>
#include<cmath>
using namespace std;
const int MaxM=1e6+5,MaxN=1e4+5;
int n,x,maxx,a[MaxM],b[MaxN];
void work(int x){
for(int i=1;i*i<x;i++)
if(x%i==0)a[i]++,a[x/i]++;
int m=sqrt(x);
if(m*m==x)a[m]++;//x是完全平方数,单独考虑
}
void print(){
for(int i=1;i<=maxx;i++)
if(b[a[i]]<i)b[a[i]]=i;//b[t]表示出现t次的最大因子
for(int i=n-1;i>=1;i--)//递推
b[i]=max(b[i],b[i+1]);
for(int i=1;i<=n;i++)cout<<b[i]<<endl;
}
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>x;
if(maxx<x)maxx=x;
work(x);
}
print();
return 0;
}