ps:题面收集于民间
第一题:差分数组
题目描述
生牛得到了一个长度为 n n n 的只包含正整数的数组 a = { a 1 , a 2 , … , a n } a=\left\{a_{1}, a_{2}, \ldots, a_{n}\right\} a={a1?,a2?,…,an?}. 他将对数组执行下列的操作直到数组只剩下一个数字:
- 假设当前数组长度为 l l l, 则对于所有的 1 ≤ i ≤ l ? 1 1 \leq i \leq l-1 1≤i≤l?1, 按 i i i 从小到大的顺序令 a i = a_{i}= ai?= a i + 1 ? a i a_{i+1}-a_{i} ai+1??ai? 井删除 a i a_i ai?.
请你写一个程序帮助牛牛计算最后剩下的数字是几, 由于答案可能很大, 你只需输出答案对 1 0 9 + 7 10^{9}+7 109+7 取摸的结果即可。
输入描述:
第一行输入一个正整数
n
n
n 。
1
≤
n
≤
5
×
1
0
3
,
1
≤
a
i
≤
1
0
9
1 \leq n \leq 5 \times 10^{3}, 1 \leq a_{i} \leq 10^{9}
1≤n≤5×103,1≤ai?≤109
输出描述:
输出一个数表示最终的答案。
样例
输入
4
1 2 3 4
输出
0
解释:第一次操作后数组变成了{1,1,1},第二次操作后变成{0,0},第三次操作后变成{0},此时只剩下一个元素,所以输出答案0。
输入
3
5 3 2
输出
1
解释:第一次操作后数组变成{-2,-1},第二次操作后数组变成 {1},此时只剩下一个元素,所以输出答案1。
思路
由于数据 1 ≤ n ≤ 5 × 1 0 3 1 \leq n \leq 5 \times 10^{3} 1≤n≤5×103比较小,两重 f o r for for循环暴力复杂度为 O ( ( n ? ( n + 1 ) / 2 ) O((n*(n+1)/2) O((n?(n+1)/2)大概是 1 0 7 10^7 107常数比较小可过,每次把数组长度 ? 1 -1 ?1,然后更新数组中的每个数,记得取模,最后数组只剩一个输出就行了。(!!!!注意减法过程中可能出现负数,负数mod要先+mod再%mod,我看好多人都死在这上面了,,
参考代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
int n;
ll a[5005];
int main()
{
cin >> n;
for (int i = 1; i <= n; i++)
{
cin >> a[i];
}
int len = n;
while (len > 1)
{
for (int i = 1; i < len; i++)
{
a[i] = (a[i + 1] - a[i] + mod) % mod;
}
len--;
}
cout << (a[1] + mod) % mod << endl;
return 0;
}
/*
4
1 2 3 4
0
3
5 3 2
1
*/
第二题:跳跳乐
题目描述
给出一个
n
n
n 个节点
m
m
m 条边的有向连通图, 节点编号
1
1
1 到
n
n
n, 保证图中没有环也没有重
边。 现在
A
l
i
c
e
Alice
Alice 和
B
o
b
Bob
Bob 在这个图上玩游戏, 首先由一个人将
1
1
1号节点涂色, 另一个人可以在上 一个人最后一次涂色的节点出边所指向的节点中任选一个并涂色。两人交替染色,谁最后能将
n
n
n号节点染色,谁就是赢家。
例如下面这个图:

n = 5 n=5 n=5, 假设由 A l i c e Alice Alice 开始, 且游戏过程为 A l i c e Alice Alice 涂 1 1 1, B o b Bob Bob 涂 2 2 2, A l i c e Alice Alice 涂 3 3 3, B o b Bob Bob 涂 5 5 5 游戏结束, 由 B o b Bob Bob获胜。
输入描述
T T T组输入,输入两个整数 n n n和 m m m分别表示点数和边数,接下来 m m m条边 ( a , b ) (a,b) (a,b),最后一行输入先手是谁,其中( T ≤ 10 , 1 ≤ N ≤ 10000 , M ≤ 10 × N , 1 ≤ a , b ≤ N T \leq 10,1 \leq N \leq 10000, M \leq 10 \times N,1 \leq a, b \leq N T≤10,1≤N≤10000,M≤10×N,1≤a,b≤N)。
输出描述
输出一个人名作为答案, A l i c e Alice Alice或者 B o b Bob Bob表示赢家的名字。(其中每次策略都会选择最优)
样例
输入
1
5 6
1 2
1 3
2 3
2 4
3 5
4 5
Alice
输出
Bob
解释: A l i c e Alice Alice先涂 1 1 1, B o b Bob Bob涂 2 2 2, A l i c e Alice Alice涂 3 3 3, B o b Bob Bob涂 5 5 5,游戏结束 B o b Bob Bob获胜。
输入
1
3 2
1 2
2 3
Alice
输出
Alice
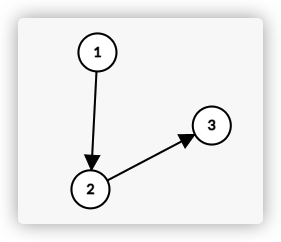
解释: A l i c e Alice Alice先涂 1 1 1, B o b Bob Bob涂 2 2 2, A l i c e Alice Alice涂 3 3 3,游戏结束 A l i c e Alice Alice获胜。(如图:
)
思路
显然是一个图上博弈问题,考虑拓扑排序和
s
g
sg
sg函数。
先把边反向,然后从
n
n
n号点开始拓扑排序求
s
g
sg
sg函数即可,
s
g
[
i
]
sg[i]
sg[i]表示先手选了第
i
i
i个点是否能必胜,
s
g
[
i
]
=
1
sg[i]=1
sg[i]=1为必胜,
0
0
0为必输,然后拓扑排序更新的时候就是,如果
x
x
x点相连的点中只要存在一个点的
s
g
sg
sg值为
1
1
1,那么
s
g
[
x
]
=
0
sg[x]=0
sg[x]=0,否则
s
g
[
x
]
=
1
sg[x]=1
sg[x]=1,最后按照
s
g
[
1
]
sg[1]
sg[1]和先手是谁输出谁赢即可。
参考代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int n, m, l;
int to[N], h[N], s[N], d[N], sg[N];
void add(int x, int y)
{
to[++l] = y, h[l] = s[x], s[x] = l;
}
int main()
{
int T;
cin >> T;
while (T--)
{
l = 0;
cin >> n >> m;
for (int i = 1; i <= m; i++)
{
int x, y;
cin >> x >> y;
add(y, x);
d[x]++;
}
d[n] = 0;
string ch;
cin >> ch;
int fg = 0;
if (ch == "Alice")
{
fg = 1;
}
for (int i = 1; i <= n; i++)
{
sg[i] = 1;
}
sg[n] = 1;
queue<int> Q;
Q.push(n);
while (!Q.empty())
{
int x = Q.front();
Q.pop();
for (int i = s[x]; i; i = h[i])
{
d[to[i]]--;
sg[to[i]] = sg[to[i]] & (sg[x] ^ 1);
if (!d[to[i]])
{
Q.push(to[i]);
}
}
}
if ((!sg[1] && !fg) || (sg[1] && fg))
{
puts("Alice");
}
else
{
puts("Bob");
}
for (int i = 1; i <= n; i++)
{
s[i] = d[i] = sg[i] = 0;
}
}
return 0;
}
/*
1
5 6
1 2
1 3
2 3
2 4
3 5
4 5
Alice
Bob
1
3 2
1 2
2 3
Alice
Alice
*/