T1：
问题 A: 方程 f(x)的根(equation)
题目描述
求方程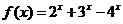
在[1，2]内的根。
?
输入
输入[1，2]的区间端点（也就是1和2），用一个空格隔开。
输出
输出方程 f(x)=0 的根，x 的值精确小数点 10 位。
样例输入
1 2
样例输出
请自行求解。
提示
2x可以表示成exp(x*log(2))的形式（需包含cmath库）。
题解
看到该题，首先想到的就是二分（当然，大多数方程求根的算法都和二分有关）。由于并不知道该函数在[1,2]上有几个解，因此普遍的做法是先划分小区间，判断可能有多少个根，再通过二分，求出各个根。第二种方式就是用数学方法证明其在该区间的单调性，然后直接二分也可以。我用的就是第二种方法（好吧，其实我做这道题的时候没有想到可能有很多解，所以也没法证明单调性，但是实验证明：该区间只存在一个解）。
参考代码
#include<cstdio>
#include<cmath>
#define MAXN 0.0000000000001
using namespace std;
double l,r;
double figure(double x)
{
return exp(x*(log(2)))+exp(x*(log(3)))-exp(x*(log(4)));
}
int main()
{
scanf("%lf%lf",&l,&r);
while(r-l>MAXN)
{
double mid=(l+r)/2;
if(figure(mid)<0) r=mid;
else l=mid;
}
printf("%.10f",l);
return 0;
}
T2：
问题 B: 骨牌问题（dominoes）
题目描述
??? 有2xn的一个长方形方格,要用若千1x2的骨牌铺满方格。例如,n=3时,为2x3方格，此时用3个1x2的骨牌铺满方格,共有3种铺法,见图。
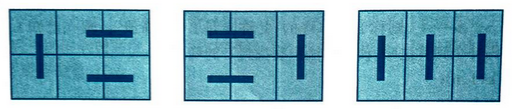
??? 编程,输入n(1≤n≤30），输出铺法总数。
?
输入
一行一个正整数n。
输出
一行一个整数，表示答案。
样例输入
3
样例输出
3
题解
该类型的题目都可以考虑用DP，有些题层数较高，n却不大，可以考虑二进制压缩的DP。由于该题只有2层，所以直接扫描一遍即可。由于对第一层而言，每一格只可能是上下型的上，左右型的左或右，所以dp的第二维开三层，0表示上，1表示左，2表示右。转移方程也就十分明显了。
参考代码
#include<cstdio>
#define LL long long
using namespace std;
LL dp[1000][3],n;
int main()
{
scanf("%lld",&n);
dp[1][0]=1ll;
for(int i=2;i<=n;i++)
{
dp[i][0]=dp[i-1][0]+dp[i-1][2];
dp[i][1]=dp[i-1][0]+dp[i-1][2];
dp[i][2]=dp[i-1][1];
}
printf("%lld",dp[n][0]+dp[n][1]+dp[n][2]);
return 0;
}
T3：问题 C: 大神排队（queue）
目描述
??? 现在共有n个同学要排成一列,每个同学有两个属性:影响力和承受能力。给一个同学造成的心理创伤指数等于所有在他前面同学的影响力之和减去他的承受能力。
??? 请安排一下排队顺序，尽量使受到心理创伤最大的同学少受创伤。
输入
??? 第1行是整数n,表示同学人数。
??? 第2~n+1行,每行两个自然数,分别是该同学的影响力和承受能力。
输出
????输出1行1个整数,为你安排的顺序中受到心理创伤最大的同学受到的创伤。
样例输入
3
10 3
2 5
3 3
样例输出
2
提示
【数据规模】
??? 对于100%的数据满足:1≤n≤50000，1≤影响力≤10000，1≤承受能力≤109。
题解
这道题乍一看是搜索题，但一看数据范围，就知道肯定是贪心了。首先我们来考虑两个人的情况（假定两人编号为A，B，防御力为F，攻击力为G）。那么只可能是A在前，造成的影响最大值为A.F-B.G，或者说B在前，造成结果B.F-A.G。我们假设A在前，为了使结果最优，必然得满足：A.F-B.G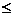
B.F-A.G，移项之后就是：A.F+A.GB.F+B.G。所以我们按照F和G的和作为关键字拍一遍序，即可得到答案中的组合。最后扫描一遍心里伤害，即可得出答案。值得注意的一点，因为第一个人之前没有人了，影响力之和为0，所以第一个人的影响力应该为其防御力的相反数。
?
参考代码
#include<algorithm>
#include<cstdio>
#define LL long long
using namespace std;
struct node
{
LL ata,ret;
int num;
}a[500100];
int n;LL minn=0,s=0;
bool comp1(node p,node q)
{
if(p.ata+p.ret<q.ata+q.ret) return 1;
else return 0;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
LL u,v;
scanf("%lld%lld",&u,&v);
a[i].num=i;
a[i].ata=u;a[i].ret=v;
}
sort(a+1,a+n+1,comp1);
minn=-a[1].ret;
s=a[1].ata;
for(int i=2;i<=n;i++)
{
if(s-a[i].ret>minn) minn=s-a[i].ret;
s+=a[i].ata;
}
printf("%lld",minn);
return 0;
}
T4：问题 D: 新约瑟夫游戏（josephus）
题目描述
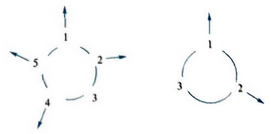
????? 你一定听说过经典的“约瑟夫”问题吧?现在来组织一个皆大欢喜的新游戏(图9.4- 5):假设n个人站成一圈,从第1人开始交替的去掉游戏者，但只是暂时去掉(例如，首先去掉2),直到最后剩下唯一的幸存者为止。幸存者选出后,所有比幸存者号码高的人每人将得到1块钱,并且永久性地离开,其余剩下的人将重复以上过程，比幸存者号码高的人每人将得到1块钱后离开。一旦经过这样的过程后,人数不再减少,最后剩下的那些人将得到2块钱。请计算一下组织者一共要付出多少钱?
????? 如图所示,第一轮有5人,幸存者是3,所以4、5得到1块钱后离开,下一轮幸存者仍然是3,因此没有人离开,所以每人得到2块钱,总共要付出2+2x 3=8块钱。
?
输入
一行一个整数n,不超过32767。
输出
一行一个整数,不超过65535,表示总共要付出多少钱。
样例输入
10
样例输出
13
题解
首先，肯定有一种证明方式，能够证明无论是从谁开始，最后剩下的人数一定是一样的。其实很好想（此处可略过），由于答案可以视为两部分相加，第一部分为每个人的一块金币（至少可以得到），第二部分则为剩下的人的一块金币。
因此，问题就转化为求：最后剩下几人（显而易见...）。
首先考虑最简单的方法：模拟。我用的方法是用队列模拟。假设n轮后还剩下k个人，那么编号小于等于k的人不可能出去，也就是说，此时队列中的初值为1~k。由于游戏规则为隔人才出，因此可以将满足条件的人编号加在队尾，不符合的直接出队，如此循环，直到人数不变，就可以得到下一次结果k1，如果k=k1，
那么就是说剩下的人数不变，那ans即为n+k；反之则令k=k1，重复上述过程，即可得到答案。
参考代码
#include<cstdio>
#include<queue>
using namespace std;
queue<int>q;
int a[100000],n,win=999999999;
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) q.push(i);
while(1)
{
while(q.size()>1)
{
q.push(q.front());
q.pop();q.pop();
}
if(win==q.front())
{
printf("%d",n+win);
return 0;
}
win=q.front();q.pop();
for(int i=1;i<=win;i++) q.push(i);
}
}
这种进、退、退的思路，在许多循环题中都有体现。
参考代码2
#include<cstdio>
using namespace std;
int n,a[66000],b[66000],ans=0,f[66000];
int main()
{
scanf("%d",&n);
a[1]=1;
for(int i=2;i<=n;i++)
{
a[i]=(a[i-1]+1)%i+1;
if(a[i]==i) f[i]=i;
else f[i]=f[a[i]];
}
ans=n+f[n];
printf("%d",ans);
return 0;
}
除了模拟以外，还可以用公式的思想来直接顺推，此处暂不叙述，给出代码以供参考。
T4： 问题 E: 开心的金明
题目描述
??? 金明今天很开心,家里购置的新房就要领钥匙了,新房里有一间他自己专用的很宽敞的房间。更让他高兴的是，妈妈昨天对他说:“你的房间需要购买哪些物品,怎么布置,你说了算,只要不超过N元钱就行”。今天一早金明就开始做预算,但是他想买的东西太多了,肯定会超过妈妈限定的N元。于是,他把每件物品规定了一个重要度,分为5等:用整数1~5表示,第5等最重要。他还从因特网上查到了每件物品的价格(都是整数元)。他希望在不超过N元(可以等于N元)的前提下,使每件物品的价格与重要度的乘积的总和最大。
??? 设第j件物品的价格为v[j],重要度为w[j],共选中了k件物品,编号依次为j1,j2, ...,jk, 则所求的总和为:v[j1]xw[j1]+v[j2]xw[j2]...+v[jk]xw[jk]。
??? 请帮助金明设计一个满足要求的购物单。
输入
??? 第1行2个正整数n和m,用一个空格隔开,其中n(n≤30000)表示总钱数,m(m≤25)为希望购买物品的个数。
??? 从第2行到第m+1行,第j行给出了编号为j-1的物品的基本数据,每行有2个非负整数v和p。其中,v表示该物品的价格( v ≤ 10000);p表示该物品的重要度(1~5),中间用一个空格隔开。
输出
??? 一行一个正整数，为不超过总钱数的物品的价格与重要度乘积的总和的最大值，一定不超过108。
样例输入
1000 5
800 2
400 5
300 5
400 3
200 2
样例输出
3900
题解
这道题其实就是一个简单的背包问题，我们可以人为的将每个物品的价值定为，这样就与最基本的01背包无区别了。
关键词 ： 01背包
参考代码
#include<cstdio>
#define LL long long
using namespace std;
int n,m;
struct node
{
LL val,num;
}a[30];
LL dp[30010],maxn=-1;
LL max1(LL p,LL q) { return p>q?p:q; }
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
scanf("%lld%lld",&a[i].val,&a[i].num);
for(int j=0;j<=n-a[i].val;j++)
{
dp[j]=max1(dp[j],dp[j+a[i].val]+a[i].val*a[i].num);
maxn=max1(maxn,dp[j]);
}
}
printf("%lld",maxn);
return 0;
}
T6：问题 F: 奇怪的电梯
题目描述
大楼的每一层楼都可以停电梯，而且第?i?层楼（1<=i<=N）上有一个数字?Ki（0<=Ki<=N）。电梯只有四个按钮：开，关，上，下。上下的层数等于当前楼层上的那个数字。当然，如果不能满足要求，相应的按钮就会失灵。例如：3 3 1 2 5?代表了?Ki（K1=3,K2=3,……），从一楼开始。在一楼，按“上”可以到?4?楼，按“下”是不起作用的，因为没有-2?楼。那么，从A?楼到?B?楼至少要按几次按钮呢？
输入
共有二行，第一行为三个用空格隔开的正整数，表示?N,A,B(1≤N≤200, 1≤?A,B≤N)，第二行为?N?个用空格隔开的正整数，表示?Ki。
输出
一行，即最少按键次数,若无法到达，则输出-1。
样例输入
5 1 5
3 3 1 2 5
样例输出
3
题解
经典题。直接暴击搜索，再加上记忆化，即可求出答案。
（不水了）看到这道题，很容易想到链表，但是又容易出现无限循环的情况，所以我选择直接用普通数组来搜索。搜索可以按照层数来搜，如果满足条件（没有飞天或者遁地），就有机会通过这一层到达那一层，这也就是递归的规则。这道题数据范围并不大，但是细节很多。首先是跳多少层，显而易见最多不超过200层，因此超过200层直接return，同时一个简单优化，当你发现有一个min时，一旦按的层数多于min，那肯定不是最优的，所以也可以return。同时如果该层曾经走过，并且标记未被消除，那也不能再走，最后当层数为b时，更新答案（不要让ans清零），然后return。而判断循环的一个简单方法，假设当前层数为k，由f层转移而来，即将到达z层，如果z=k，那说明在走循环了，只有当zk时，才可以按键穿层。
换成代码语言就是：
void dfs(int k,int f,int dep)
{
if(dep>200) hint=1;
if(hint==1) return;
if(dep>min1) return;
if(vis[k]) return;
if(k==b)
{
if(dep<min1) min1=dep;
return;
}
vis[k]=1;
if(pd(k+get[k]))
if(k+get[k]!=f)
dfs(k+get[k],k,dep+1);
if(pd(k-get[k]))
if(k-get[k]!=f)
dfs(k-get[k],k,dep+1);
vis[k]=0;
}
最后-1的情况要单独判断。
因此本题不复杂，但是细节多。
参考代码：
#include<cstdio>
using namespace std;
int n,a,b,min1=999999999;
int get[300],vis[300],hint=0;
bool pd(int k)
{
return (k<=n)&&(k>0);
}
void dfs(int k,int f,int dep)
{
if(dep>200) hint=1;
if(hint==1) return;
if(dep>min1) return;
if(vis[k]) return;
if(k==b)
{
if(dep<min1) min1=dep;
return;
}
vis[k]=1;
if(pd(k+get[k]))
if(k+get[k]!=f)
dfs(k+get[k],k,dep+1);
if(pd(k-get[k]))
if(k-get[k]!=f)
dfs(k-get[k],k,dep+1);
vis[k]=0;
}
int main()
{
scanf("%d%d%d",&n,&a,&b);
for(int i=1;i<=n;i++) scanf("%d",&get[i]);
if(a==b)
{
printf("0");
return 0;
}
dfs(a,-1,0);
if(hint==1||min1==999999999) printf("-1");
else printf("%d",min1);
return 0;
}
T7:问题 G: 团伙
题目描述
在某城市里住着 n 个人，任何两个认识的人不是朋友就是敌人，而且满足：
1、我朋友的朋友是我的朋友；
2、我敌人的敌人是我的朋友；
所有是朋友的人组成一个团伙。告诉你关于这 n 个人的 m 条信息，即某两个人是朋友，或者某两个人是敌人，请你编写一个程序，计算出这个城市最多可能有多少个团伙？
输入
第1 行为 n 和 m，1<n<1000,1<=m<=100000；
以下 m 行，每行为 p、x、y，p 的值为 0 或 1，p 为 0 时，表示 x 和 y 是朋友，p 为 1 时，表示 x 和 y 是敌人。
输出
一个整数，表示这 n 个人最多可能有几个团伙。
样例输入
6 4
1 1 4
0 3 5
0 4 6
1 1 2
样例输出
3
题解：
这是一道并查集的板题，考的知识点很单一，但是细节方面很容易错（一旦少一个find，样例能过，但是绝对WA）。首先是写find函数（见下），然后注意将1到2n的fa值都定为本身。之后如果是朋友，首先就find（x），find（y），再建立关系（我的find是实时更新fa值的），对于敌人，我们可以把y和x+n建立联系，同理，也可以把x与y+n建立联系，具体的是要先find，再建立，然后注意是，最后只用找没有父亲的点，就是一个组群了。
参考代码
#include<cstdio>
using namespace std;
int n,m,fa[100010],vis[100001],ans=0,head[100001];
int x[1000000],y[1000000],p[1000000];
int find(int v)
{
if(fa[v]==v) return v;
else return fa[v]=find(fa[v]);
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n*2;i++) fa[i]=i;
for(int i=1;i<=m;i++){
scanf("%d%d%d",&p[i],&x[i],&y[i]);
if(p[i]==0)
{
x[i]=find(x[i]);y[i]=find(y[i]);
fa[x[i]]=y[i];
}
else
{
fa[find(x[i]+n)]=find(y[i]);
fa[find(y[i]+n)]=find(x[i]);
}
}
for(int i=1;i<=n;i++)
{
if(fa[i]==i) ans++;
}
printf("%d",ans);
return 0;
}
T8问题 H: 遭遇战
题目描述
??????小林和小华在一个nx?n的矩形方格里玩游戏,矩形左上角为(0,0),右下角为(n-1,n-1)。两人同时进入地图的随机位置,并以相同速度进行走位。为了隐蔽性,两人都不会再走自己走过的格子。如果两人向某一方向前进,那么他们会跑到不能跑为止,当不能跑的时候,小林会向右转,小华则会向左转,如果不能跑,则不再动。现在已知两人进人地图的初始位置和方向，请算出两人遭遇的位置。
输入
??? 第1行1个正整数t,表示测试数据组数,1≤t≤10。
??? 接下来的t组数据，每组数据的第1行包含1个整数n, 1≤n≤1000。
??? 第2行包含3个整数x、y和d,表示小林的初始位置和一开始跑的方向。其中，d=0表示东;d=1表示南;d=2表示西;d=3表示北。
??? 第3行与第2行格式相同,但描述的是小华。
输出
??? 输出t行,若会遭遇,则包含两个整数,表示他们第一次相遇格子的坐标，否则输出“-1”。
样例输入
2
2
0 0 0
0 1 2
4
0 1 0
3 2 0
样例输出
-1
1 3
提示
【问题分析】
??? 设置两个布尔型数组，分别记录模拟每个人走过的格子。如果两人没有相遇并且还可以跑，就让他们按照规则一直跑下去。
题解
问题分析很简单，实现起来却有点麻烦。主要是这道题中人可以一直转（走不动），而不是只转一次就结束。其实也很好理解，转身是不计入时间的。由于两人的方向改变相反，因此假定有一个方向常量d，则一个是+1，一个是-1，然后取模4并且取正，就可以得到下一个方向。然后建立两个map地图，分别记录小华和小林走过的地方，最后当两人相遇（交叉而过不算，看样例1）于同一格子，或者两人都走不动了，就可以统计答案，return了（在dfs函数中）。思路真的很简单，我却满打满算写了3个。
这道题同T7，不难，但是特别需要细心！
参考代码
#include<cstdio>
#include<cstring>
using namespace std;
int vis1[1001][1001],vis2[1001][1001],n,t;
int d1,d2,pk_a=0,pk_b=0;
int d1x[4]={0,1,0,-1};
int d1y[4]={1,0,-1,0};
int d2x[4]={0,-1,0,1};
int d2y[4]={1,0,-1,0};
int x1,x2,y1,y2;
bool pd(int x,int y)
{
return (x<=n)&&(x>0)&&(y<=n)&&(y>0);
}
void bfs()
{
while(1)
{
if(x1==x2&&y1==y2)
{
printf("%d %d\n",x1-1,y1-1);
pk_a=0;pk_b=0;
break;
}
if(pk_a==1&&pk_b==1)
{
printf("%d\n",-1);
pk_a=0;pk_b=0;
break;
}
int x11=x1,y11=y1;
int x22=x2,y22=y2;
if(!pk_a)
{
int pd1=0;
x11=x1+d1x[d1];y11=y1+d1y[d1];
if(!pd(x11,y11)||vis1[x11][y11])
{
for(int i=0;i<3;i++)
{
d1=(d1+1)%4;
x11=x1+d1x[d1];y11=y1+d1y[d1];
if(!pd(x11,y11)||vis1[x11][y11]) continue;
pd1=1;break;
}
}
else pd1=1;
if(pd1==0)
{
x11=x1;y11=y1;
pk_a=1;
}
vis1[x11][y11]=1;
}
if(!pk_b)
{
int pd1=0;
x22=x2+d2x[d2];y22=y2+d2y[d2];
if(!pd(x22,y22)||vis2[x22][y22])
{
for(int i=0;i<3;i++)
{
d2=(d2+1)%4;
x22=x2+d2x[d2];y22=y2+d2y[d2];
if(!pd(x22,y22)||vis2[x22][y22]) continue;
pd1=1;break;
}
}
else pd1=1;
if(pd1==0)
{
x22=x2;y22=y2;
pk_b=1;
}
vis2[x22][y22]=1;
}
x1=x11;x2=x22;y1=y11;y2=y22;
}
}
int main()
{
scanf("%d",&t);
while(t--)
{
memset(vis1,0,sizeof(vis1));
memset(vis2,0,sizeof(vis2));
scanf("%d",&n);
scanf("%d%d%d",&x1,&y1,&d1);
scanf("%d%d%d",&x2,&y2,&d2);
if(x1==x2&&y1==y2)
{
printf("%d %d\n",x1,y1);
continue;
}
if(d2==3) d2=1;
else if(d2==1) d2=3;
x1++;x2++;y1++;y2++;
bfs();
}
}