一、问题描述

给定一个链表，返回链表开始入环的第一个节点。如果链表无环，则返回 null。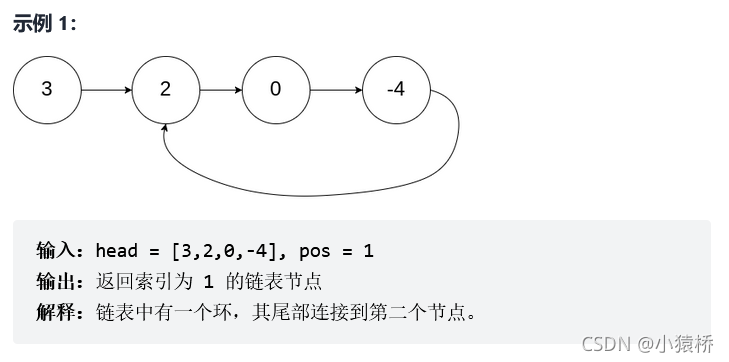在这里插入图片描述
其中pos为圆环的入口点序号，但返回值并不是用pos，返回节点地址。

二、如何判断链表是否带环

假设链表带环，那么这个链表就会一直循环下去；假设这个链表没有环，那么这个链表最终就会走到空。基于此，我们定义两个指针（快慢指针），fast与slow。循环一直往后走，当fast为空或者fast->next为NULL时，代表无环；当fast==slow时，即相遇，即有环。

#fast和slow每次走几步合适#
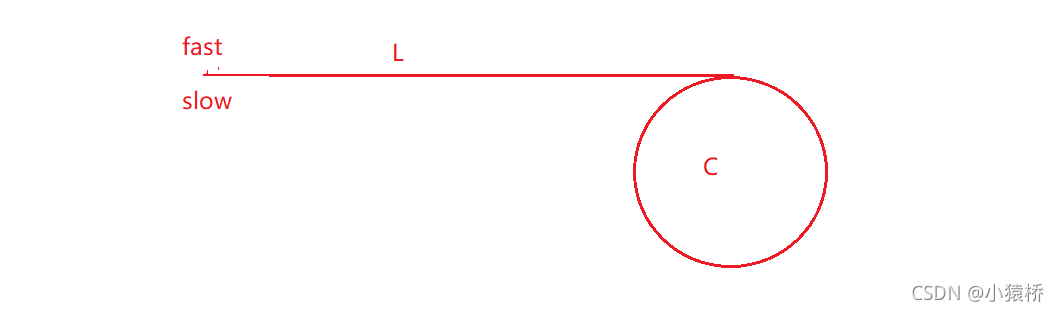
在这里插入图片描述

slow很明显每次只走一步最合适，那么fast该走几步，是否一定能相遇？
首先，当fast进环时，slow走到了L的中点。如下图：
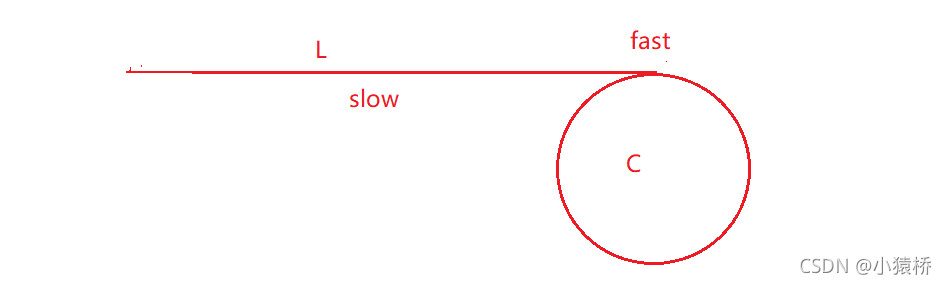
在这里插入图片描述

此后，fast开始转圈圈，当slow开始进环，fast可能在环内任意一点。然后fast开始追逐slow。（思考：为什么在slow的一圈之内，fast必追上slow？）
如果fast一次走2步，fast和slow必能一圈之内相遇。因为速度差为1，他们之间的距离每次缩减1，所以必能相遇。

如果fast一次走3步，这里就要分情况讨论：
在这里插入图片描述此时fast和slow相距C-X，距离依次减小：
第一圈：
C-X
C-X-2
C-X-4
…
0或者-1
当走到最后一步为0，则能相遇；为-1，代表反超，错过。即C-X为偶数时能相遇，否则不能。继续考虑第二圈是否能追上。

第二圈：
在这里插入图片描述此时fast比slow快1，距离为C-1。此时按每步距离减2
C-1
C-3
C-5
…
0/-1
同理，当最后一步为0，则能相遇；为-1，代表反超，错过，而此次错过则为永远错过。（因为接下来距离又会变成C-1）。所以当C-1为偶数时，第二圈能遇见，否则，永远不可能相遇。

三、如何求进环点

1、这里先给出结论：
在这里插入图片描述
如图所示，假设meet为相遇点，则一个指针从head开始走，一个指针从meet开始走，一定会在进环点相遇。接下来给出证明。

2、结论证明：
在这里插入图片描述相遇时slow走的距离：L+X
fast走的距离：NC+L+X
有NC+L+X = 2(L+X)----->L = NC-X ------>L = (N-1)C+C-X
注意：这里N代表N圈，由于不知道圈C和L的大小，所以无法判断在相遇前，fast转了多少圈。
由L = (N-1)C+C-X 可知两指针head和meet必会在进环口相遇。

四、代码实现

struct ListNode *detectCycle(struct ListNode *head) 
{
    struct ListNode* slow = head;
    struct ListNode* fast = head;
    while(fast && fast->next)     //fast和fast->next的顺序不能反
    {                             //不然就会出现访问空指针的情况
        slow = slow->next;
        fast = fast->next->next;
        if(fast == slow)         //有环
        {
            struct ListNode* meet = fast;   //相遇点
            while(meet != head)
            {
                meet = meet->next;
                head = head->next;
            }
            return meet;
        }
    }
    return NULL;
}