二叉树路径
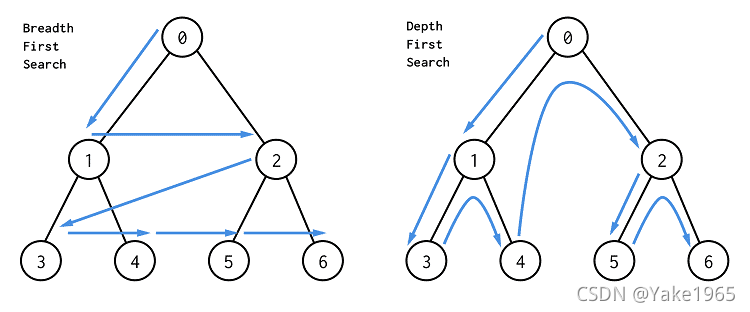
深度优先搜索(DFS)和广度优先搜索(BFS)
左边是 BFS,按照层进行搜索;图右边是 DFS,先一路走到底,然后再回头搜索。
257. 二叉树的所有路径
112. 路径总和
113. 路径总和 II
437. 路径总和 III
面试题 04.12. 求和路径
988. 从叶结点开始的最小字符串
124. 二叉树中的最大路径和
687. 最长同值路径
543. 二叉树的直径
257. 二叉树的所有路径
DFS
一、空结点处理
1、递归中空结点返回
class Solution:
def binaryTreePaths(self, root: TreeNode) -> List[str]:
def dfs(node, path):
if not node: return # 空结点返回
path += str(node.val)
if not (node.left or node.right): # 叶子结点
res.append(path)
return
dfs(node.left, path + '->')
dfs(node.right, path + '->')
res = []
dfs(root, '')
return res
2、判断空结点,递归中不含空结点
class Solution:
def binaryTreePaths(self, root: TreeNode) -> List[str]:
def dfs(node, path):
path += str(node.val)
if not (node.left or node.right): # 叶子结点
res.append(path)
node.left and dfs(node.left, path + '->') # 判断空结点
node.right and dfs(node.right, path + '->')
res = []
dfs(root, '')
return res
二、路径全局变量与传参
全局变量需要拷贝与回溯,参数为不可变对象时不需要,参数各是各的,如上。参数是列表,使用 path = path + [root.val] 添加元素,事实上 path 已经变了。
1、path 定义成 list
class Solution:
def binaryTreePaths(self, root: TreeNode) -> List[str]:
def dfs(node):
path.append(node.val)
if not (node.left or node.right): # 叶子结点
res.append(path[:]) # copy
node.left and dfs(node.left)
node.right and dfs(node.right)
path.pop() # 回溯
path = []
res = []
dfs(root)
return ['->'.join(map(str,x)) for x in res]
2、path 定义成 str
class Solution:
def binaryTreePaths(self, root: TreeNode) -> List[str]:
def dfs(node):
nonlocal path
path += str(node.val) if node == root else '->' + str(node.val)
if not (node.left or node.right): # 叶子结点
res.append(path)
node.left and dfs(node.left)
node.right and dfs(node.right)
path = path.rsplit('->', 1)[0] # 回溯
path = ''
res = []
dfs(root)
return res
BFS
class Solution:
def binaryTreePaths(self, root: TreeNode) -> List[str]:
q = deque([(root, str(root.val))]) # 携带路径元组
res = []
while q:
cur, path = q.popleft()
if not cur.left and not cur.right: # 叶子结点
res.append(path)
cur.left and q.append((cur.left, path + '->' + str(cur.left.val)))
cur.right and q.append((cur.right, path + '->' + str(cur.right.val)))
return res
112. 路径总和
根结点到叶子结点的路径上值的和 :在叶子结点上判断。
方法一:递归 DFS
class Solution:
def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
if not root:return False
if not root.left and not root.right: # 叶子结点
return root.val == targetSum
# 问题转化为左右子树递归
return self.hasPathSum(root.right, targetSum - root.val) or self.hasPathSum(root.left, targetSum - root.val)
方法二:广度优先搜索 BFS
class Solution:
def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
if not root: return False
q = deque([(root, targetSum)]) # 通过元组携带值
while q:
cur, tem = q.popleft()
tem -= cur.val
if not cur.left and not cur.right: # 叶子结点
if tem == 0: return True
continue
cur.left and q.append((cur.left, tem))
cur.right and q.append((cur.right, tem))
return False
113. 路径总和 II
方法一:DFS
cclass Solution:
def pathSum(self, root: Optional[TreeNode], targetSum: int) -> List[List[int]]:
def dfs(cur, tem):
# 如果 path 作为参数传入,此处用 path = path + cur.val,就不用 copy 和回溯了。
path.append(cur.val)
tem -= cur.val
if not (cur.left or cur.right or tem):
res.append(path[:]) # copy
cur.left and dfs(cur.left, tem)
cur.right and dfs(cur.right, tem)
path.pop() # 回溯
if not root:return []
res , path = [], []
dfs(root, targetSum)
return res
方法二:BFS
class Solution:
def pathSum(self, root: TreeNode, sum: int) -> List[List[int]]:
class Solution:
def pathSum(self, root: Optional[TreeNode], targetSum: int) -> List[List[int]]:
if not root: return []
res = []
q = deque([(root, [], targetSum)]) # 结点,路径,路径和
while q:
cur, path, tem = q.popleft()
# path += [cur.val]
# path.append(cur.val) # 列表 +=,append 对象不变 !!!
path = path + [cur.val] # 对象变了
tem -= cur.val
# 如果是叶子节点,同时和为零。
if not cur.left and not cur.right and not tem:
res.append(path) # 保存路径
cur.left and q.append((cur.left, path, tem))
cur.right and q.append((cur.right, path, tem))
return res
面试题 04.12. 求和路径
437. 路径总和 III
方法一:
class Solution:
def pathSum(self, root: TreeNode, targetSum: int) -> int:
def calPathSum(root, sum):
if not root: return 0
tmp = 0
sum -= root.val
if sum == 0:
tmp += 1
return tmp + calPathSum(root.left, sum) + calPathSum(root.right, sum)
if not root: return 0
return calPathSum(root, targetSum) + self.pathSum(root.left, targetSum) + self.pathSum(root.right, targetSum)
方法二:
class Solution:
def pathSum(self, root: TreeNode, targetSum: int) -> int:
def f(r, s):
if r:
s = [i + r.val for i in s] + [r.val]
return s.count(targetSum) + f(r.left, s) + f(r.right, s)
return 0
return f(root, [])
124. 二叉树中的最大路径和
687. 最长同值路径
543. 二叉树的直径
vector<vector> res;
vector<vector> pathSum(TreeNode *root, int targetSum)
{
vector path;
dfs(root, targetSum, path);
return res;
}
void dfs(TreeNode*root, int sum, vector path)
{
if (!root)
return;
sum -= root->val;
path.push_back(root->val);
if (!root->left && !root->right && sum == 0)
{
res.push_back(path);
return;
}
dfs(root->left, sum, path);
dfs(root->right, sum, path);
}
437. 路径总和 III
双重递归:先调用dfs函数从root开始查找路径,再调用pathsum函数到root左右子树开始查找
没有通过
class Solution:
def __init__(self):
self.count = 0
def pathSum(self, root: TreeNode, sum: int) -> int:
@lru_cache(None)
def dfs(node, sum):
sum -= root.val
# 注意不要return,因为不要求到叶节点结束,所以一条路径下面还可能有另一条
if sum == 0:
self.count += 1 # 如果找到了一个路径全局变量就 + 1
node.left and dfs(node.left, sum)
node.right and dfs(node.right, sum)
if not root: return 0
dfs(root, sum)
self.pathSum(root.left, sum)
self.pathSum(root.right, sum)
return self.count
- 从叶结点开始的最小字符串
换汤不换药,套用模板1
vector path;
string smallestFromLeaf(TreeNode *root)
{
dfs(root, “”);
sort(path.begin(), path.end()); //升序排序
return path[0];
}
void dfs(TreeNode *root, string s)
{
if (!root)
return;
s += ‘a’ + root->val;
if (!root->left && !root->right)
{
reverse(s.begin(), s.end()); //题目要求从根节点到叶节点,因此反转
path.push_back(s);
return;
}
dfs(root->left, s);
dfs(root->right, s);
}
二、非自顶向下
124. 二叉树中的最大路径和
/left,right分别为根节点左右子树最大路径和,注意:如果最大路径和<0,意味着该路径和对总路径和做负贡献,因此不要计入到总路径中,将它设置为0
int res = INT_MIN; //注意节点值可能为负数,因此要设置为最小值
int maxPathSum(TreeNode *root)
{
maxPath(root);
return res;
}
int maxPath(TreeNode *root) //以root为路径起始点的最长路径
{
if (!root)
return 0;
int left = max(maxPath(root->left), 0);
int right = max(maxPath(root->right), 0);
res = max(res, left + right + root->val); //比较当前最大路径和与左右子树最长路径加上根节点值的较大值,更新全局变量
return max(left + root->val, right + root->val); //返回左右子树较长的路径加上根节点值
}
687. 最长同值路径
int longestUnivaluePath(TreeNode *root)
{
if (!root)
return 0;
longestPath(root);
return res;
}
int longestPath(TreeNode *root)
{
if (!root)
return 0;
int left = longestPath(root->left), right = longestPath(root->right);
// 如果存在左子节点和根节点同值,更新左最长路径;否则左最长路径为0
if (root->left && root->val == root->left->val)
left++;
else
left = 0;
if (root->right && root->val == root->right->val)
right++;
else
right = 0;
res = max(res, left + right);
return max(left, right);
}
543. 二叉树的直径
int res1 = 0;
int diameterOfBinaryTree(TreeNode *root)
{
maxPath(root);
return res1;
}
int maxPath(TreeNode *root)
{
// 这里递归结束条件要特别注意:不能是!root(而且不需要判断root为空,因为只有非空才会进入递归),因为单个节点路径长也是0
if (!root->left && !root->right)
return 0;
int left = root->left ? maxPath(root->left) + 1 : 0; //判断左子节点是否为空,从而更新左边最长路径
int right = root->right ? maxPath(root->right) + 1 : 0;
res1 = max(res, left + right); //更新全局变量
return max(left, right); //返回左右路径较大者
}
以上就是二叉树路径问题的
作