1. 冒泡排序

冒泡排序

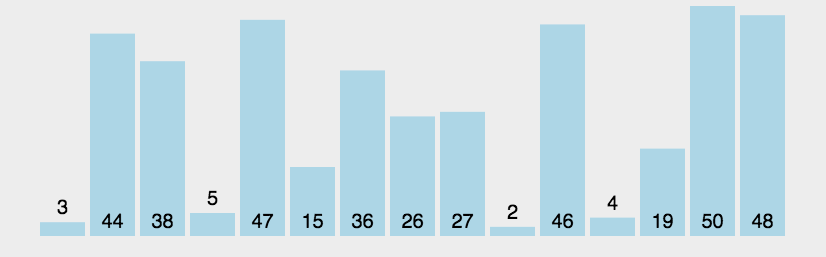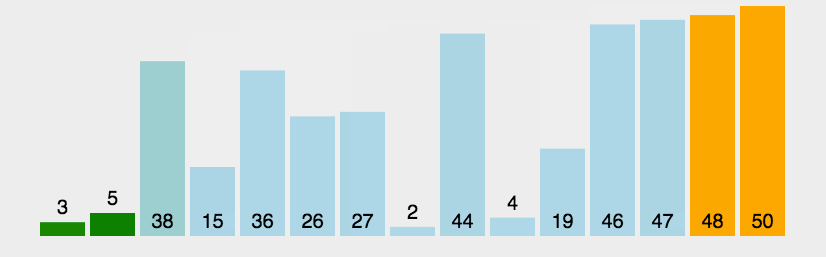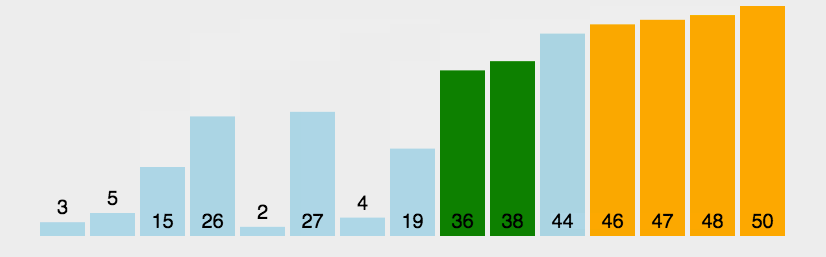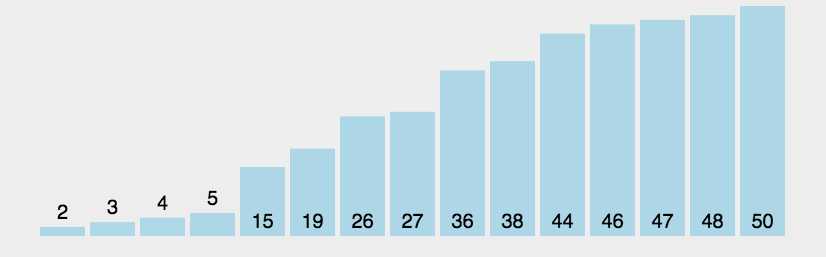
比较相邻的元素，前一个比后一个大（或者前一个比后一个小）调换位置

public static void bubbleSort(int a[]) {
   int n = a.length;
   for (int i = n - 1; i > 0; i--) {
       for (int j = 1; j <= i; j++) {
           if (a[j] < a[j - 1]) {
               int t = a[j];
               a[j] = a[j - 1];
               a[j - 1] = t;
           }
       }
   }
}

2. 选择排序

选择排序
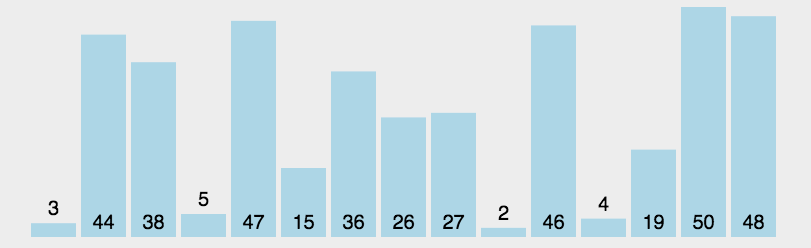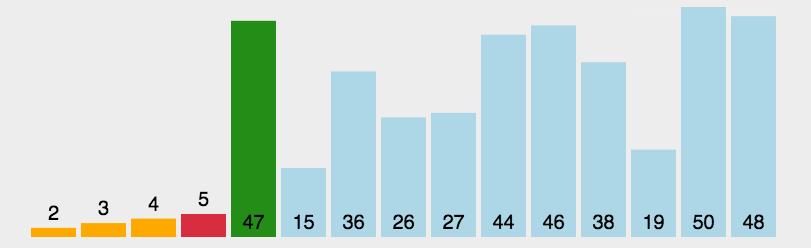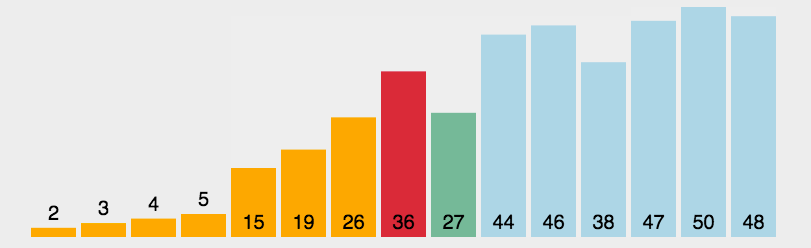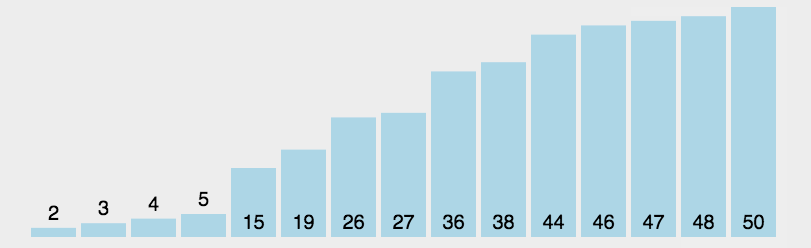
思想：

找到一个最小值与最前面一个数进行交换
在第2个数~最后一个数中，找到次小值与第二个数进行交换
依次类推… 直到最后

public static void choiceSort(int a[]) {
	int n = a.length;
    for (int i = 0; i < n; i++) {
        int idx = i;//记录每次需要交换的点的下标
        //在 i+1 到 n-1 中的数寻找最小值的下标
        for (int j = i + 1; j < n; j++) {
            if (a[j] < a[idx]) {
                idx = j;//记录最小值的
            }
        }
        int t = a[i];
        a[i] = a[idx];
        a[idx] = t;
    }
}

3. 插入排序

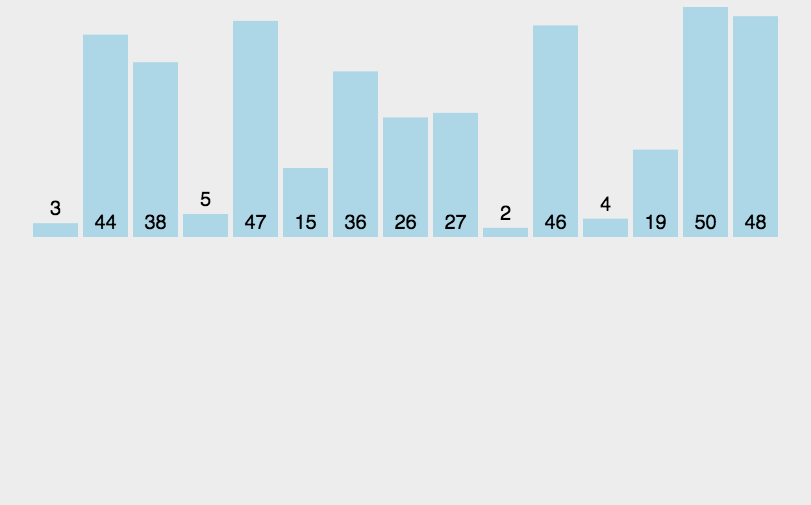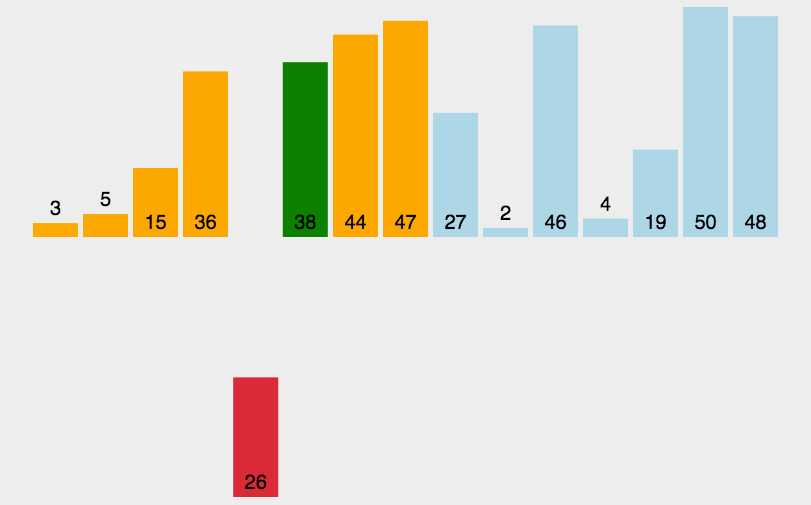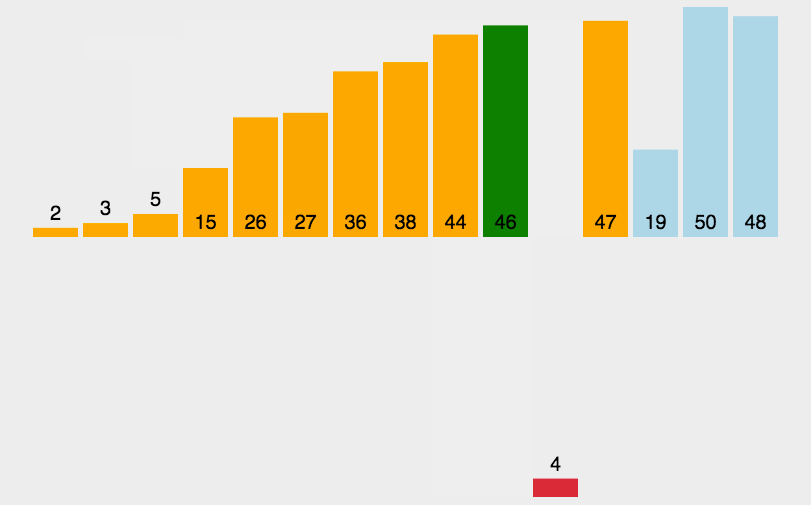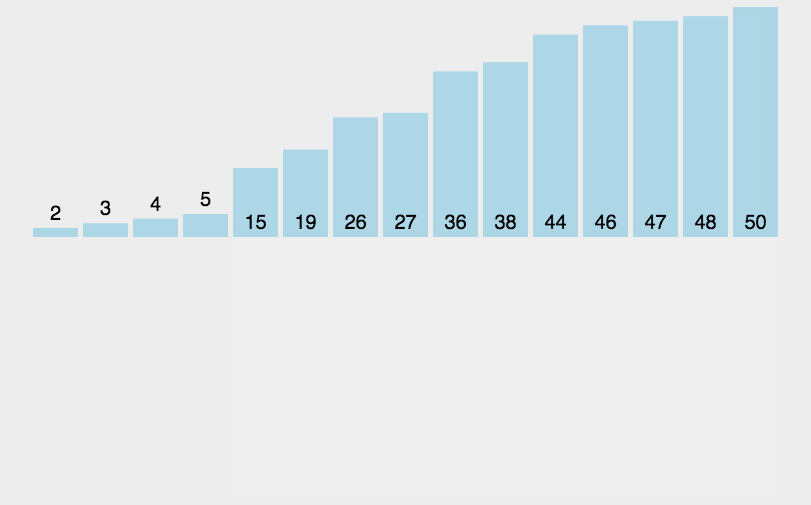
插入排序思想：前面设置好一个已经排好序的部分，如上图橙色部分所示，依次遍历未排序的部分，将当前遍历到的数抽出来，插入到已经排好序的数组中。

public static void insertSort(int a[]) {
    int n = a.length;
    for (int i = 1; i < n; i++) {
        int t = a[i];//暂存a[i]的值
        int idx = i - 1;//已经排好序数组的最后一个位置
        //从idx往前遍历，保证不越界，并且大于a[i]
        while (idx >= 0 && a[idx] > t) {
        	//将这些数往后挪一个位置出来，腾出位置放a[i]
            a[idx + 1] = a[idx];
            idx--;
        }
        //因为上面的while循环是要求满足a[idx]>t，所以结束的时候说明a[i] > a[idx]，所以将a[i]的值放到idx + 1的位置。
        a[idx + 1] = t;
    }
}

4. 堆排序

堆排序
上图是大顶堆的演示，原理是相同的。

堆：一棵完全二叉树。
完全二叉树：除了最后一层不满，上面是满二叉树，但最后一层从左到右。

独特的存储方式：
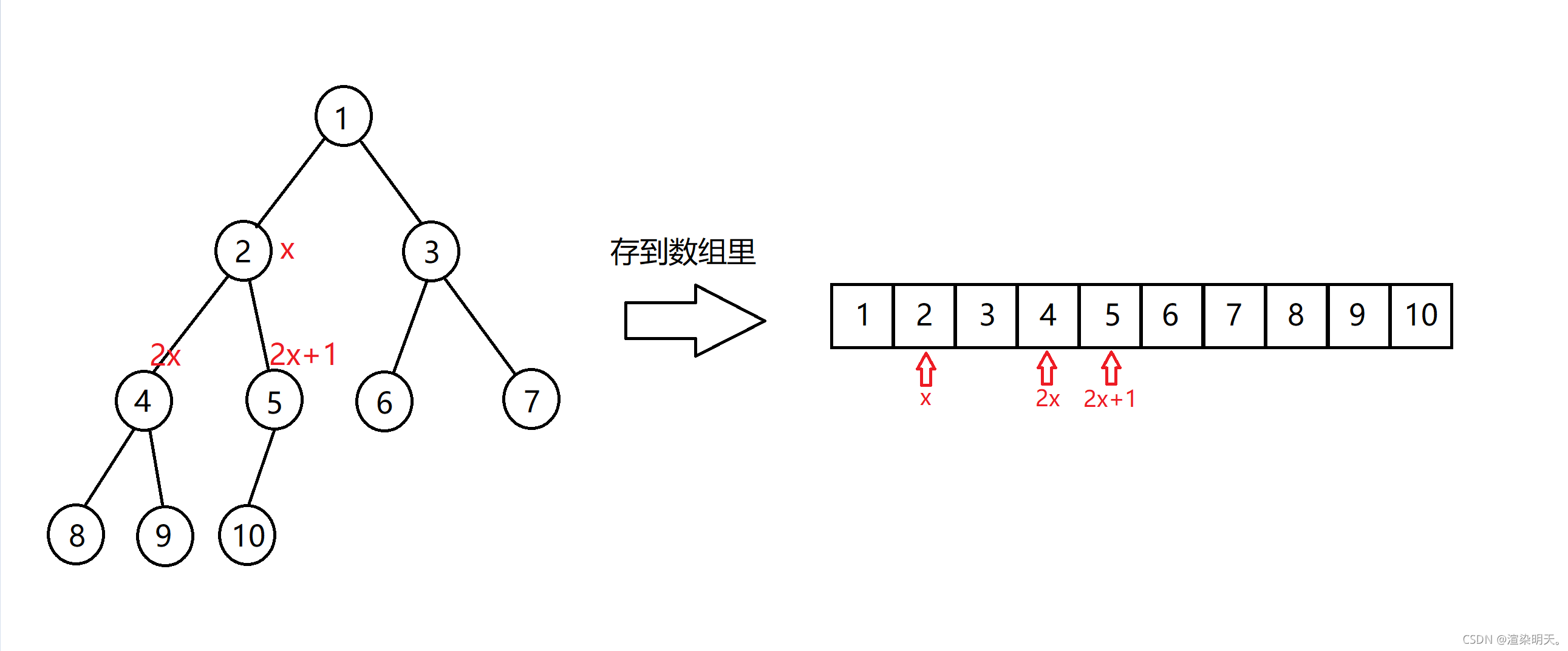
在这里插入图片描述

作业题目是小顶堆。
个人习惯：以下标1作为堆顶元素，感觉比用下标0作为堆顶元素舒服，2x和2x+1，如果是0的话，左子节点也是0，需要操作一波，我比较懒，所以就，dddd

解释一下代码中的 down(x) 操作：
down顾名思义，即将当前节点往下调整，因为要维护一个堆，就要保证
根节点是小于等于左右子节点 (小顶堆)
即： $a [x] \leq a [2 ? x]$ && $a [x] \leq a [2 ? x + 1]$
所以要从前往后遍历一遍，找到左右子节点和根节点的最小值，如果最小值出现在左右字节点中，就要与根节点位置进行交换。递归的down就行

建堆的两种方式：
1. O(nlogn)建堆，一个一个点插入。
在堆中插入一个数x：
heap[++size] = x;//将需要插入的数放到堆的最后面，进行up操作
up(x);
2. O(n) 的方式建堆

public class HeapSort {
    public static int n;
    public static int h[] = {0, 25, 30, 11, 7, 22, 16, 18, 33, 40, 55};
    public static void down(int u){
        int t = u;
        if (u << 1 <= n && h[t]> h[u << 1]) t = u << 1;
        if ((u << 1 | 1) <= n && h[t] > h[u << 1 | 1]) t  = u << 1 | 1;
        if (t != u) {
            int tmp = h[u];
            h[u] = h[t];
            h[t] = tmp;
            down(t);
        }
    }
    public static void main(String args[]){
        n = h.length;
        n--;
        //建堆
        for (int i = n / 2; i >= 1; i--) down(i);

        int len = n;
        //依次提出堆顶元素
        for (int i = 1; i <= len; i++) {
            System.out.print(h[1] + " ");
            h[1] = h[n--];//删除堆顶元素
            down(1);//将堆顶元素down一遍
        }
    }
}

5. 百钱百鸡问题

问题提出：公元前5世纪末，中国古代数学家张丘建在他的《算经》中提出了著名的 “百钱买百鸡问题”：鸡翁一，值钱五，鸡母一，值钱三，鸡雏三，值钱一，百钱买百鸡，问翁、母、雏各几何？即一百个铜钱买了一百只鸡，其中公鸡一只5钱、母鸡一只3钱，雏鸡一钱3只，问一百只鸡中公鸡、母鸡、雏鸡各多少? 算法的伪代码如下：

for x = 0 to 100
	for y = 0 to 100
     	for z = 0 to 100
         	if  (x+y+z=100)  and  (5*x + 3*y + z/3 = 100)  then
           		System.out.println("  "+x+"  "+y+"  "+z)
         	end if

实验要求： 对上述算法做出改进以提高算法的效率，要求将算法的时间复杂性由Ο(n3)降为 Ο(n2)，并将改进的算法编程实现。
思想： 将a, b, c 转换成 a, b, (100 - a - b);

public class moneyCock {
    public static void main(String[] args) {
        for (int i = 0; i <= 100; i++) {
            for (int j = 0; j <= 100; j++) {
                boolean edge = 100 - i - j >= 0 && 100 - i - j <= 100;
                boolean money = i * 5 + j * 3 + (100 - i - j) / 3 == 100;
                boolean flagTimes = (100 - i - j) % 3 == 0;
                if (edge && money && flagTimes) {
                    System.out.println("公鸡数量" + i + ' ' + "母鸡数量为" + j + ' ' + "小鸡数量为" + (100 - i - j));
                }
            }
        }
    }
}