[数据结构与算法]基本数据结构-队列(C语言实现)

队列的概念

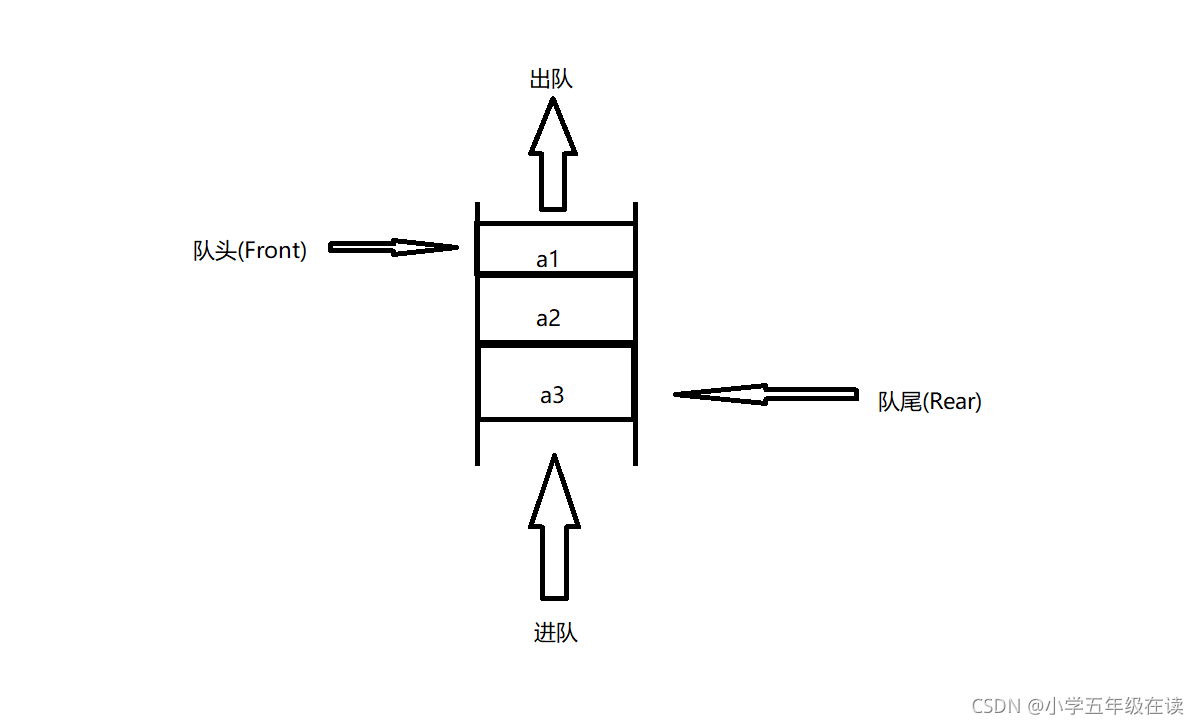
队列是一种特殊的线性表，特殊之处在于它只允许在表的前端（front）进行删除操作，而在表的后端（rear）进行插入操作，和栈一样，队列是一种操作受限制的线性表。进行插入操作的端称为队尾，进行删除操作的端称为队头。是一种先进先出的线性表
插入元素称为入队；删除元素称为出队

队列示意图

队列的实现

• 使用链表的实现

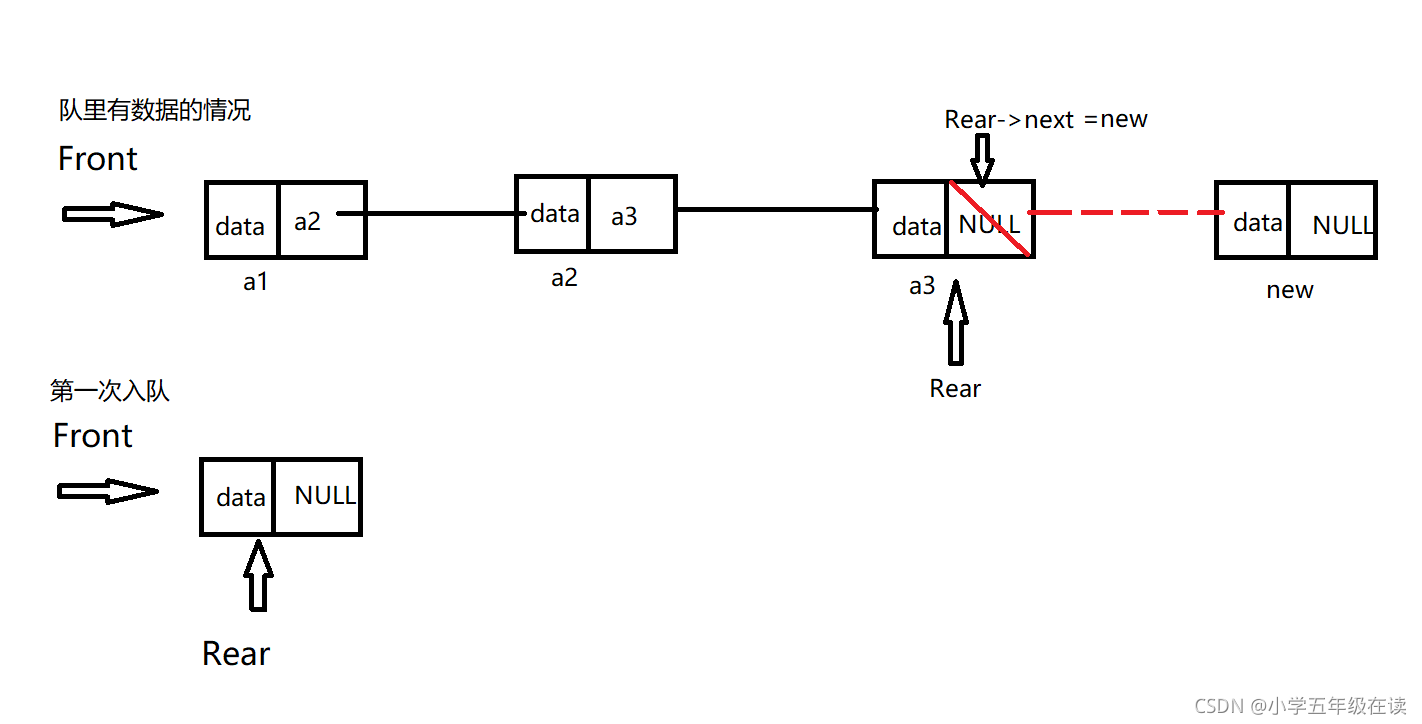
这句代码的实际目的用一张图来表示
 q->rear->next = new;

#include <stdio.h>
#include <stdlib.h>
//定义队列元素的结构体
typedef struct queue {
    int data;
    struct queue *next;
} *queue;
//定义队首和队尾指针
typedef struct queue_list {
    queue front;
    queue rear;
} *queue_list;
//队列初始化
queue init() {
    queue_list q = (queue) malloc(sizeof(queue));
    q->front = q->rear = NULL;
    return q;
}
//进队操作
void EnQueue(queue_list q, int num) {
    queue new = (queue) malloc(sizeof(queue));
    new->data = num;
    new->next = NULL;
    if(q->front==NULL){
        q->front=new;
        q->rear=new;
    } else {
        //将new成为当前尾部节点的下一节点
        q->rear->next = new;
        //将当前尾部节点更新成new
        q->rear = new;
    }
}
//出队操作
void DeQueue(queue_list q) {
    if (q->front) {
        //获取队列首地址
        queue p = q->front;
        free(p);
        //释放完首元素修改首地址指向后面一个元素地址
        q->front = q->front->next;
    } else {
        return;
    }
}
//查看队列内的元素
void print(queue_list L){
    //直接获取队列首地址
    queue q=L->front;
    if(q) {
        while (q) {
            printf("%d", q->data);
            q = q->next;
        }
        printf("\n");
    } else{
        printf("队内无元素\n");
    }
}
int main() {
    queue_list head;
    head = init();
    EnQueue(head, 3);
    EnQueue(head, 5);
    EnQueue(head, 1);
    EnQueue(head, 1);
    print(head);
    DeQueue(head);
    print(head);
    return 0;
}

• 数组实现（循环队列）
  每次尾指针都指向最后一个有效元素的下一个地址
  顺序队列必须是循环队列使用下标对队列最大值取模来不断的循环地址

#include <stdio.h>
#include <stdlib.h>
//数组最大长度
#define MAXSIZE 6
typedef struct {
    int *data;
    int front;
    int rear;
} *queue;

//初始化队列
queue init() {
    queue new = (queue) malloc(sizeof(queue));
    new->data = (int *) malloc(sizeof(queue) * MAXSIZE);
    new->front = new->rear = 0;
    return new;
}

//入队
void InsertQueue(queue q, int num) {
    //判断是否已满
    if ((q->rear + 1) % MAXSIZE == q->front) {
        printf("队列已满\n");
        return;
    }
    if (q->front) {
        q->data[(q->rear)] = num;
        q->rear = (q->rear + 1) % MAXSIZE;
    } else {
        q->data[(q->rear)] = num;
        q->rear = (q->rear + 1) % MAXSIZE;
    }
}

//出队
void DeQueue(queue q) {
    q->front = (q->front + 1) % MAXSIZE;
}

//遍历
void print(queue q) {
    int index = q->front;
    if (q->front == q->rear) {
        printf("队列中无数据\n");
        return;
    } else {
        while (index != q->rear) {
            printf("%d", q->data[index]);
            index = (index + 1) % MAXSIZE;;
        }
    }
    printf("\n");
}

int main() {
    queue L;
    L = init();
    InsertQueue(L, 3);
    InsertQueue(L, 1);
    InsertQueue(L, 5);
    print(L);
    DeQueue(L);
    print(L);
    InsertQueue(L, 5);
    InsertQueue(L, 5);
    InsertQueue(L, 5);
    InsertQueue(L, 5);
    InsertQueue(L, 5);
    InsertQueue(L, 5);
    print(L);
    return 0;
}