2.1 线性表及其表现
一、什么是线性表
1. 一元多项式的表示
方法1:顺序存储结构直接表示 —— 适用于多项式中每一项的指数较小的情况
用一维数组的各分量表示多项式各项,即数组元素a[i]表示多项式中项
x
i
x^i
xi的系数
a
i
a_i
ai?;两个多项式相加,就是两个数组对应的分量相加
例1,表示
f
(
x
)
=
4
x
5
?
3
x
2
+
1
f(x)=4x^5-3x^2+1
f(x)=4x5?3x2+1,则利用数组可以有如下表示:
| 下标i | 0 | 1 | 2 | 3 | 4 | 5 | ... |
| a[i] | 1 | 0 | -3 | 0 | 0 | 4 | ... |
方法2:顺序存储结构表示非零项
用二维数组的各分量表示多项式各项,即数组元素a[i][j]中,下标i不一定表示多项式中第i+1项,a[i][0]表示多项式系数
a
i
a^i
ai,a[i][1]表示多项式中项
x
i
x^i
xi的指数i的值。这样,每个数组元素a[i][j]指向非零项。这样,每一个多项式可以看成是一个
(
a
i
,
i
)
(a_i,i)
(ai?,i)二元组的集合。
在该法中,最号按照指数大小有序存储。
例2,表示
P
1
(
x
)
=
9
x
12
+
15
x
8
+
3
x
2
P_1(x)=9x^{12}+15x^8+3x^2
P1?(x)=9x12+15x8+3x2和
P
2
(
x
)
=
26
x
19
?
4
x
8
?
13
x
6
+
82
P_2(x)=26x^{19}-4x^8-13x^6+82
P2?(x)=26x19?4x8?13x6+82
使用多行2列的二维数组表示,如下
| P1(x)的表示 | ||||
| 下标i | 0 | 1 | 2 | ... |
| 系数a^i | 9 | 15 | 3 | ... |
| 指数 | 12 | 8 | 2 | ... |
| P2(x)的表示 | |||||
| 下标i | 0 | 1 | 2 | 3 | ... |
| 系数a^i | 26 | -4 | -13 | 82 | ... |
| 指数 | 19 | 8 | 6 | 0 | ... |
方法3:链表结构存储非零项
链表中的每一个结点存储多项式中的一个非零项,包括系数和指数两个数据域以及一个指针域。
在例2中,可以声明链表
struct PolyNode {
int coef; // 系数
int expon; // 指数
Polynomial link; // 指针
}
typedef struct PolyNode *Polynomial;

2. 表示一元多项式的启示
- 同一问题可以有不同的表示和储存方法
- 有序线性序列可以用线性表
3. 线性表:由同类型数据元素构成有序序列的线性结构
- 线性表的长度:线性表中元素个数
- 空表:线性表没有元素
- 表头:线性表起始位置
- 表尾:线性表结束位置
4. 线性表的抽象数据类型描述
- 类型名称:线性表
- 数据对象集:线性表是
n个元素构成的有序序列( a 1 , a 2 , . . . , a n a_1,a_2,...,a_n a1?,a2?,...,an?) - 操作集:线性表
L用List表示,整数i表示位置,元素x用ElementType表示 - 线性表的基本操作:
List MakeEmpty (); // 初始化一个空线性表
ElementType FindKth (int k, List L); // 根据位序K,返回相应元素
int Find (ElementType X, List L); // 在线性表L中查找X的第一次出现位置
void Insert (ElementType X, int i, List L); // 在位序i前插入一个新元素X
void Delete (int i, List L); // 删除指定位序i的元素
int Length (List L); // 返回线性表L的长度n
5. 线性表的顺序存储:可以利用数组的连续存储空间顺序存放线性表的各元素
-
直观表示

-
数据结构
struct LNode { ElementType Data[MAXSIZE]; int Last; // 线性表中最后一个元素的索引号 }; typedef struct LNode* List; // 声明指向线性表的指针的数据类型 struct LNode L; // L线性表 List PtrL; //指向线性表的指针 // 访问下标为i的元素 L.Data[i]; PtrL->Data[i]; // 线性表的长度 L.Last+1; PtrL->Last+1; -
算法
-
初始化(建立空的顺序表)
List MakeEmpty() { List PtrL; PtrL = (List )malloc( sizeof(struct LNode)); // malloc创建一个用于存放一个线性表的空间,并且PtrL指向该空间首地址 PtrL->Last = -1; // 目前该空间是空顺序表,没有任何元素 return Ptrl; } -
查找
/* 输入:ElementType X 要查找的元素 * List PtrL 指向线性表首地址的指针 * 输出:线性表中对应元素的索引号 */ int Find(ElementType X, List PtrL) { int i = 0; // i是线性表中元素的索引号 // 遍历线性表,查找元素X while (i <= PtrL->Last && PtrL->Data[i] != X) { i++; } if (i > PtrL->Last) { return -1; // 没找到元素X,返回-1 } else { return i; // 找到元素X,返回对应的索引号 } }
复杂度:平均比较次数为 ( n + 1 ) / 2 (n+1)/2 (n+1)/2,平均时间性能为 O ( n ) O(n) O(n)
运气好,线性表中第一个元素是所查找的元素,比较次数是1;运气好,线性表中最后一个元素是所查找的元素,比较次数是n。
-
插入元素(在索引号为
i的位置上插入一个值为X的新元素)
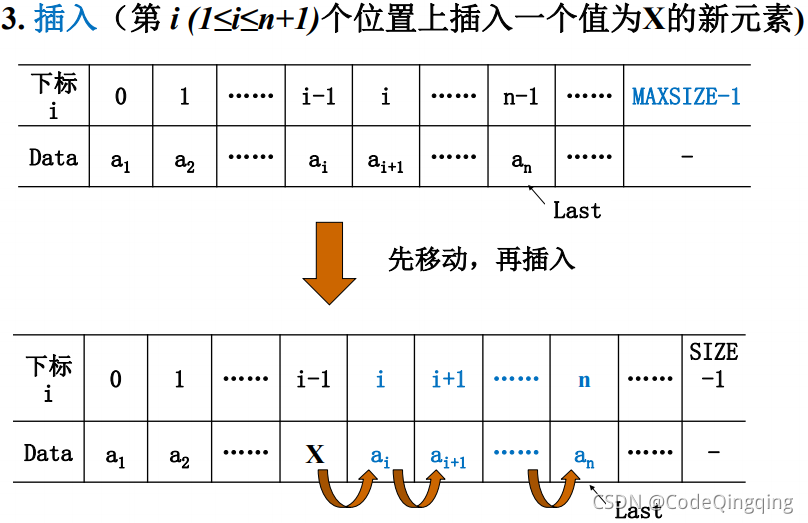
/* 输入:ElementType X 要插入的元素 * int i 要插入的位置(元素索引号) * List PtrL 指向线性表首地址的指针 * 输出: */ void Insert(ElementType X, int i, List PtrL) { int j; // 判断插入操作是否可行 if (PtrL->Last == MAXSIZE-1) { // 线性表可用空间已满,不能插入 printf("线性表已满\n"); return; } if (i < 1 || i > PtrL->Last + 2) { // i<1时会影响下面的移动元素的操作;i > PtrL->Last + 2时说明插入的位置在合理范围外,该合理范围为插入元素后的索引号的取值范围,即0~PtrL->Last + 1 printf("插入位置不合法\n"); return; } /* 实施插入操作 */ // 先将a_i~a_n范围内的所有元素整体向后移动一格,且遍历的顺序从后往前 for (j = PtrL->Last; j >= i-1; j--) { // j的起始位置是线性表的最后一个元素的索引号。一般地,与PtrL->Last相比,MAXSIZE较大,故可以放心向后移动元素而不用担心丢失最后一个元素 PtrL->Data[j+1] = PtrL->Data[j]; // 在线性表中,从后往前取相邻的两个元素,并将前面的元素复制到后面的位置上 } PtrL->Data[i-1] = X; // 插入新元素 PtrL->Last++; // Last保存新线性表末尾元素的索引号 return; }复杂度:平均移动次数为 n / 2 n/2 n/2,平均时间性能为 O ( n ) O(n) O(n),主要由
for循环决定 -
删除第
i个元素 a i a_i ai?
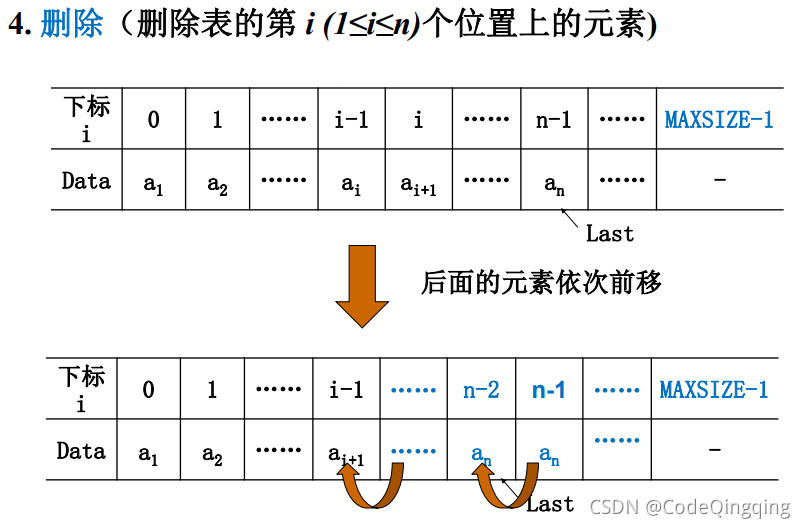
/* 输入:int i 删除第i个项a_i(对应元素索引号为i-1) * List PtrL 指向线性表的指针 * 输出:void */ void Delete(int i, List PtrL) { int j; if (i < 1 || i > PtrL->Last + 1) { // 检查删除元素的位置的合法性 printf("不存在第%d个元素\n"); return; } for (j = i; j <= PtrL->Last; j++) { PtrL->Data[j-1] = PtrL->Data[j]; // 将a_i+1 ~ a_n依次向前移动 } PtrL->Last--; // 更新Last的值 return; }复杂度:平均移动次数为 ( n ? 1 ) / 2 (n-1)/2 (n?1)/2,平均时间性能为 O ( n ) O(n) O(n)
6. 线性表的链式存储实现
- 该存储方式只要求两个元素在逻辑上相邻,而不要求在物理上相邻
- 插入、删除元素不需要移动数据元素,秩序奥修改“链”
- 数据结构:

struct LNode {
ElementType Data;
List Next;
};
typedef struct LNode* List;
struct LNode L;
List PtrL;
- 算法
-
求单向链表长
/* 输入:List PtrL 链表表头 * 输出:int j 链表的长度 */ int Length(List PtrL) { List p = PtrL; // 指针p指向表的第一个结点 int j = 0; while (p) { // 每一次循环中,p指向下一个元素的空间,同时j加1。 p = p->Next; // 为p赋值后,在j自加前,p指向第j个结点 j++; } return j; }复杂度:时间性能为 O ( n ) O(n) O(n)
-
查找元素
(1) 按序号查找/* 输入:int K 要查找第k个结点 * List PtrL 链表表头 * 输出:List p 要查找的元素的地址 */ List FindKth(int K, List PtrL) { List p = PtrL; // p指向表头 int i = 1; while (p != NULL && i < K) { // 未找到指定序号,但i在合理范围内时,则遍历线性表 p = p->Next; i++; } if (i == k) { // 找到指定序号,返回对应的存储地址 return p; } else { // 没有找到指定序号,返回空 return NULL; } }复杂度:时间性能为 O ( n ) O(n) O(n)
(2) 按值查找
/* 输入:ElementType X 要查找的元素 * List PtrL 链表表头 * 输出:List P 要查找的元素的地址 */ List Find(ElementType X, List PtrL) { List p = PtrL; while (p != NULL && p->Data != X) { // 未找到指定的元素,且在合理的范围内,则遍历线性表 p = p->Next; } return p; // 若找到了指定元素,则返回对应的储存地址 // 若未找到指定元素,则返回NULL }
复杂度:时间性能为 O ( n ) O(n) O(n)
-
插入元素(在第
i-1个结点后插入一个值为X的新结点)
思路:- 先构造一个新结点,用
s指向; - 再找到链表的第
i-1个结点,用p指向; - 然后修改指针,在
p指向的结点后插入新结点

/* 输入:ElementType X 要插入的元素的值 * int i 在第i个结点处(第i-1个结点后面)插入新元素 * List PtrL 旧链表表头 * 输出:List PtrL 插入元素后的新链表的首地址 */ List Insert(ElementType X, int i, List PtrL) { List p, s; /* 旧链表为空时,直接插入新结点(在表头处插入结点) */ if (i == 1) { s = (List)malloc(sizeof (struct LNode)); // 申请新结点的存储空间 s->Data = X; // 设置新结点的元素值 s->Next = PtrL; // 设置新结点的Next链 return s; // 返回插入元素后新链表的首地址 } p = FindKth(i-1, PtrL); // 找到链表的第i-1个结点 /* 旧链表非空时 */ if (p == NULL) { // 找不到第i-1个结点 printf("参数i错误\n"); return NULL; } else { // 找到了第i-1个结点 s = (List)malloc(sizeof (struct LNode)); // 申请新结点的存储空间 s->Data = X; // 设置新结点的元素值 s->Next = P->Next; // 设置新结点的Next链指向旧链表的第i个结点,即新结点在第i-1个结点和第i个结点间 p->Next = s; // 旧链表的第i个结点指向新结点。27行和26行的代码顺序不可调换 return PtrL; // 返回添加元素后新链表的首地址 } } - 先构造一个新结点,用
-
删除元素(删除旧链表的第
i个位置上的结点)
思路:- 先找到链表的第
i-1个结点,用p指向; - 再用指针
s指向要被删除的结点,即p指向的结点的下一个结点; - 修改指针,使
p指向的结点指向指针s指向的结点的下一个结点; - 最后释放
s指向的结点的空间。
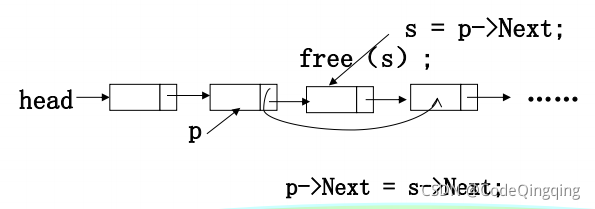
/* 输入:int i 要删除旧链表第i个结点 * List PtrL 旧链表表头 * 输出:List PtrL 返回删除结点后的新链表的首地址 */ List Delete(int i, List PtrL) { List p, s; if (i == 1) { // 若删除表头结点 s = PtrL; if (PtrL != NULL) { // 若旧链表不空,则将下一个结点的首地址当做表头地址 PtrL = PtrL->Next; } else { // 旧链表为空,无法删除结点 return NULL; } free(s); // 释放被删除的结点 return PtrL; // 返回删除结点后的新链表的表头地址 } p = FindKth(i-1, PtrL); // 查找第i-1个结点(要删除的结点的前一个结点) if (p == NULL) { // 若未找到第i-1个结点 printf("第%d个结点不存在", i-1); return NULL; } else if (p->Next == NULL) { // 找到了要删除结点的前一结点,但要删除的结点位置不在链表范围内,故不合理 printf("第%d个结点不存在", i); return NULL; } else { s = p->Next; // s指向要删除的结点 p->Next = s->Next; // 要删除的结点的前一结点链接到要删除的结点的后一结点 free(s); // 释放被删除的结点 return PtrL; // 返回删除结点后的新链表的首地址 } }复杂度:平均时间性能为 n / 2 n/2 n/2
- 先找到链表的第