A:The Child and Sequence | CF438D
题意
- 长度为
n
n
n 的序列
a
n
a_n
an?,你需要实现如下共
m
m
m 次操作:
(1)求区间和
(2)区间取模
x
x
x
(3)单点置
a
k
=
x
a_k=x
ak?=x -
1
≤
n
,
m
≤
1
0
5
1\le n,m\le 10^5
1≤n,m≤105
1
≤
a
i
≤
1
0
9
1\le a_i\le 10^9
1≤ai?≤109
思路
- 关键是区间取模怎么做,貌似是一个挺经典的题了。
考虑,对于一个数
x
x
x,每次取模,这个数字最大变为
x
2
\frac{x}{2}
2x?,所以最多取模次数是
O
(
log
?
)
O(\log )
O(log) 级别的 - 如果区间的最大值
m
x
<
x
mx<x
mx<x,那么区间取模
x
x
x 相当于没有取模。
如上两个操作就可以保证复杂度。注意我们只有单点置没有区间置。
代码
- 时间复杂度:
O
(
(
n
+
m
)
log
?
R
)
O((n+m)\log R)
O((n+m)logR)
#include<bits/stdc++.h>
using namespace std;
#define ls (p<<1)
#define rs (p<<1|1)
#define md ((l+r)>>1)
#define ll long long
const int MAX = 1e5+50;
ll aa[MAX];
ll treeSum[MAX*4];
ll treeMx[MAX*4];
void push_up(int p){
treeSum[p]=treeSum[ls]+treeSum[rs];
treeMx[p]=max(treeMx[ls],treeMx[rs]);
}
void build(int p,int l,int r){
if(l == r){
treeSum[p] = treeMx[p] = aa[l];
return;
}
build(ls,l,md);
build(rs,md+1,r);
push_up(p);
}
void update(int p,int l,int r,int u,ll k){
if(l == r){
treeSum[p] = treeMx[p] = k;
return;
}
if(u <= md)update(ls,l,md,u,k);
if(u > md)update(rs,md+1,r,u,k);
push_up(p);
}
void update2(int p,int l,int r,int ux,int uy,ll k){
if(treeMx[p] < k)return;
if(l == r){
treeSum[p] %= k;
treeMx[p] %= k;
return;
}
if(ux <= md)update2(ls,l,md,ux,uy,k);
if(uy > md)update2(rs,md+1,r,ux,uy,k);
push_up(p);
}
ll query(int p,int l,int r,int qx,int qy){
ll res = 0;
if(qx <= l && r <= qy)return treeSum[p];
if(qx <= md)res += query(ls,l,md,qx,qy);
if(qy > md)res += query(rs,md+1,r,qx,qy);
return res;
}
int main()
{
int n,m;scanf("%d%d",&n,&m);
for(int i = 1;i <= n;++i)scanf("%lld",&aa[i]);
build(1,1,n);
for(int i = 1;i <= m;++i){
ll op,t1,t2,t3;
scanf("%lld",&op);
if(op == 1){
scanf("%lld%lld",&t1,&t2);
printf("%lld\n",query(1,1,n,t1,t2));
}else if(op == 2){
scanf("%lld%lld%lld",&t1,&t2,&t3);
update2(1,1,n,t1,t2,t3);
}else{
scanf("%lld%lld",&t1,&t2);
update(1,1,n,t1,t2);
}
}
return 0;
}
B:Errich-Tac-Toe (Hard Version) | CF1450C2
题意
- 给定一个大小为
n
×
n
n\times n
n×n 的网格,每个格子要么为空,要么为
X
X
X,要么为
O
O
O
规定,出现赢局就是行 / 列上有同时有三个相同的
O
O
O 或者
X
X
X
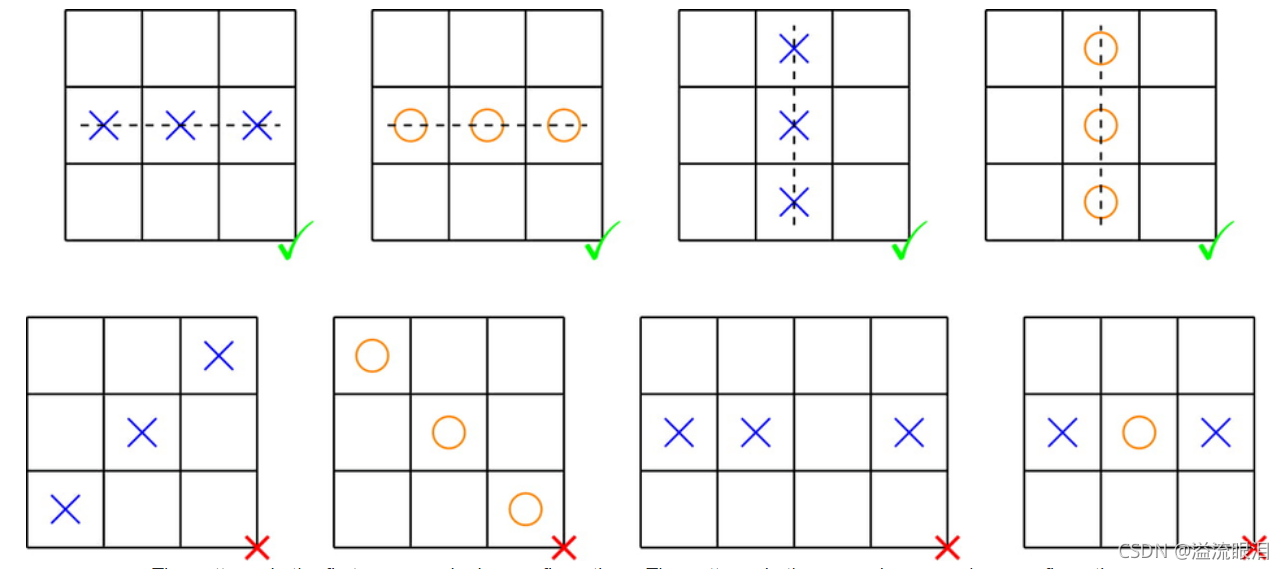 - 一次操作,你可以翻转一个
X
X
X 变成
O
O
O 或者翻转一个
O
O
O 变成
X
X
X
假设棋盘上有
k
k
k 个棋子,请在最多
?
k
3
?
\lfloor \frac{k}{3}\rfloor
?3k?? 步内让棋局没有赢局。
1
≤
n
≤
300
1\le n\le 300
1≤n≤300 - 你需要输出最后的没有赢局的局面。
思路
- 感觉如果用各种奇妙的贪心和特判的话,这题会变得特别不好做。
我们先考虑一下,如果一个局面全是
X
X
X 的话,怎么处理?
XXXXX
XXXXX
XXXXX
XXXXX
XXXXX
|
V
XXOXX
XOXXO
OXXOX
XXOXX
XOXXO
- 可以
依稀感觉到,对于
a
x
,
y
a_{x,y}
ax,y? 的棋子,我们按
(
x
+
y
)
%
3
(x+y)\%3
(x+y)%3 作为三个同余类
S
0
,
S
1
,
S
2
S_0,S_1,S_2
S0?,S1?,S2?去处理。
如果我们定
S
0
S_0
S0? 必须为
X
X
X,这样就可以保证不会有
O
O
O 的赢局
如果我们定
S
0
S_0
S0? 必须为
O
O
O,这样就可以保证不会有
X
X
X 的赢局
我们不希望有
O
O
O 与
X
X
X 的赢局,我们可以让
S
0
,
S
1
,
S
2
S_0,S_1,S_2
S0?,S1?,S2? 中的两项取出来,满足上述俩要求即可。 - 接下来是操作上限的证明
容易得到:
S
0
(
X
)
+
S
1
(
X
)
+
S
2
(
X
)
+
S
0
(
O
)
+
S
1
(
O
)
+
S
2
(
O
)
=
k
S_0(X)+S_1(X)+S_2(X)+S_0(O)+S_1(O)+S_2(O)=k
S0?(X)+S1?(X)+S2?(X)+S0?(O)+S1?(O)+S2?(O)=k
所以必定存在一对
S
t
(
X
)
,
S
t
+
1
(
O
)
S_t(X),S_{t+1}(O)
St?(X),St+1?(O),满足
S
t
(
X
)
+
S
t
+
1
(
O
)
≤
?
k
3
?
S_t(X)+S_{t+1}(O)\le \lfloor \frac{k}{3} \rfloor
St?(X)+St+1?(O)≤?3k??
当然也存在
S
t
(
O
)
,
S
t
+
1
(
X
)
S_t(O),S_{t+1}(X)
St?(O),St+1?(X) 也是满足的。
代码
- 时间复杂度:
O
(
n
2
)
O(n^2)
O(n2)
#include<bits/stdc++.h>
using namespace std;
void show(){std::cerr << endl;}template<typename T,typename... Args>void show(T x,Args... args){std::cerr << "[ " << x << " ] , ";show(args...);}
#define ll long long
const int MAX = 3e2+50;
char aa[MAX][MAX];
int main()
{
int T;scanf("%d",&T);
while(T--){
int n;scanf("%d",&n);
int k = 0;
for(int i = 1;i <= n;++i)scanf("%s",aa[i]+1);
for(int i = 1;i <= n;++i)
for(int j = 1;j <= n;++j)
if(aa[i][j] != '.')k++;
for(int t = 0;t < 3;++t){
int cnt = 0;
for(int i = 1;i <= n;++i)
for(int j = 1;j <= n;++j){
if((i+j)%3 == t && aa[i][j] == 'X')cnt++;
if((i+j+1)%3 == t && aa[i][j] == 'O')cnt++;
}
if(cnt <= k / 3){
for(int i = 1;i <= n;++i){
for(int j = 1;j <= n;++j){
if((i+j)%3 == t && aa[i][j] == 'X')aa[i][j] = 'O';
if((i+j+1)%3 == t && aa[i][j] == 'O')aa[i][j] = 'X';
printf("%c",aa[i][j]);
}
puts("");
}
break;
}
}
}
return 0;
}
C:Sonya and Problem Wihtout a Legend | CF713C
题意(在原题上增强)
思路
- 这个题目一个是改为单调不递减,一个是改为严格单调递增,但其实是等价的。
假设原数列元素有
a
<
b
<
c
a<b<c
a<b<c
我们令
a
a
≤
b
b
≤
c
c
aa\le bb\le cc
aa≤bb≤cc
其实就是相当于
a
a
<
b
b
?
1
<
c
c
?
2
aa<bb-1<cc-2
aa<bb?1<cc?2
也相当于
a
a
?
1
<
b
b
?
2
<
c
c
?
3
aa-1<bb-2<cc-3
aa?1<bb?2<cc?3
所以,我们原序列中的元素
a
i
a_i
ai? 更新为
a
i
=
a
i
?
i
a_i=a_i-i
ai?=ai??i,那么严格单调递增问题就可以转化为单调不递减序列问题。
注意到,我们问题之和
a
i
a_i
ai? 与
a
j
a_j
aj? 的差值有关,而与
a
i
a_i
ai? 的具体数值是无关的,因此可以转化。 - 有一个比较简单的例子。假设
n
=
2
n=2
n=2,有数字
a
,
b
a,b
a,b,其中
a
>
b
a>b
a>b
这个时候,答案一定是
b
?
a
b-a
b?a,方案也很简单,就是
c
∈
[
a
,
b
]
c\in[a,b]
c∈[a,b],然后让
a
,
b
a,b
a,b 都变成
c
c
c 即可。
注意到,如果数列长度比较长,为了让答案不劣,我们令
c
=
a
c=a
c=a 明显是更优的。 - 假设现在我们处理到
i
i
i 的答案了,其中
a
i
?
1
a_{i-1}
ai?1? 我们修改值变为了
a
i
?
1
′
a_{i-1}^\prime
ai?1′?
如果
a
i
≥
a
i
?
1
′
a_i\ge a_{i-1}^\prime
ai?≥ai?1′?,显然我们不需要修改。
否则,我们需要多操作
a
i
?
1
′
?
a
i
a_{i-1}^\prime-a_i
ai?1′??ai? 次操作。
?
\color{red}{*}
? 在形式上,我们可以令
a
i
?
1
′
=
a
i
a_{i-1}^\prime=a_{i}
ai?1′?=ai?,就像上面的让答案更优。但是可能会使得
a
i
?
1
′
<
a
i
?
2
′
a_{i-1}^\prime<a_{i-2}^\prime
ai?1′?<ai?2′?,但这并不妨碍我们,因为若我们令
a
i
′
=
a
i
?
1
′
a_i^\prime=a_{i-1}^\prime
ai′?=ai?1′?,也是多操作了这些步骤,且保证一定是合法的。若
a
i
?
1
′
<
a
i
?
2
′
a_{i-1}^\prime<a_{i-2}^\prime
ai?1′?<ai?2′? 成立了,我们变 假装 调整这个序列,通过如下的手段:
1 3 3 3 5 (2) 新加入了 2
因为 2 < 5 ,我们要多操作 5-2=3 次
我们假装变成这样:
1 3 3 5(5)
在形式上,我们变成这样:
1 3 3 3 (2) 2
但是我们注意到了, 3 > 2,这个序列并不是单递增了
但是我们最后两个 2 可以随便转变为 [2,5] 中的随意数字,都是可以的,我们不妨把这两个点缩成一个点
1 3 3 3 (2)
然后我们再新加进来一个 1
1 3 3 3 2 (1)
注意到,此时序列中最高值为 3 ,我们要多操作 3-1=2 次
同理,序列中最左边的那个 3 和新加进来的 1 ,可以合并成一个点,且取值 [1,3] 都是可以的,我们自然取 1 最优
所以序列新变成了:
1 (1) 3 3 2
注意,这里我们都是假装的序列。如果要求是合法的序列,我们必须取值范围要取得更劣些,就变成这样:
1 [3] 3 3 (3 3) [3]
- 从代码实现来说,就是用一个优先队列。最大元素为
x
x
x,现在新加进来一个
y
y
y
如果
x
≤
y
x\le y
x≤y,我们自然不需要修改,把
y
y
y 丢进去即可。
否则,我们需要多
x
?
y
x-y
x?y 次操作,然后把
x
x
x 丢掉,再把
y
y
y 丢进去(点合并) - CF713C 标准题解是
O
(
n
2
)
O(n^2)
O(n2) 的离散化
d
p
dp
dp,在评论区有人第一次表述了
O
(
n
log
?
n
)
O(n\log n)
O(nlogn) 的代码,但是是使用斜率和凸包分析描述的,不是很懂,但代码是相同的,这里提出自己的思考(瞎掰)。
代码
- 时间复杂度:
O
(
n
log
?
n
)
O(n\log n)
O(nlogn)
#include<bits/stdc++.h>
using namespace std;
void show(){std::cerr << endl;}template<typename T,typename... Args>void show(T x,Args... args){std::cerr << "[ " << x << " ] , ";show(args...);}
#define ll long long
const int MAX = 3e2+50;
priority_queue<int>Q;
int main()
{
int n;scanf("%d",&n);
ll ans = 0;
for(int i = 1;i <= n;++i){
int t;scanf("%d",&t);t -= i;
Q.push(t);
if(t < Q.top()){
ans += Q.top() - t;
Q.pop();
Q.push(t);
}
}
printf("%lld",ans);
return 0;
}
D:Product Oriented Recurrence | CF1182E
题意
思路
- 之前看有人牛客群里问了
f
x
=
f
x
?
1
f
x
?
2
f_x=f_{x-1}f_{x-2}
fx?=fx?1?fx?2? 的问题咋做,随机就拉到了这题…
一个很标准的矩阵快速幂的题目,会写的应该都会,稍微变变即可。 - 第一步,我们记录每个数字
f
x
=
f
1
a
×
f
2
b
×
f
3
c
×
o
t
h
e
r
s
f_x=f_1^{a}\times f_2^b\times f_3^c\times others
fx?=f1a?×f2b?×f3c?×others,算出次数
a
,
b
,
c
a,b,c
a,b,c
容易想到,对于乘积来说,次方是相加的。我们容易写出转移:
(
1
1
1
1
0
0
0
1
0
)
(
f
n
(
a
)
f
n
(
b
)
f
n
(
c
)
f
n
?
1
(
a
)
f
n
?
1
(
b
)
f
n
?
1
(
c
)
f
n
?
2
(
a
)
f
n
?
2
(
b
)
f
n
?
2
(
c
)
)
=
(
f
n
+
1
(
a
)
f
n
+
1
(
b
)
f
n
+
1
(
c
)
f
n
(
a
)
f
n
(
b
)
f
n
(
c
)
f
n
?
1
(
a
)
f
n
?
1
(
b
)
f
n
?
1
(
c
)
)
\begin{pmatrix} 1&1&1\\ 1&0&0\\ 0&1&0\\ \end{pmatrix} \begin{pmatrix} f_n(a)&f_n(b)&f_n(c)\\ f_{n-1}(a)&f_{n-1}(b)&f_{n-1}(c)\\ f_{n-2}(a)&f_{n-2}(b)&f_{n-2}(c)\\ \end{pmatrix} = \begin{pmatrix} f_{n+1}(a)&f_{n+1}(b)&f_{n+1}(c)\\ f_n(a)&f_n(b)&f_n(c)\\ f_{n-1}(a)&f_{n-1}(b)&f_{n-1}(c)\\ \end{pmatrix}
???110?101?100???????fn?(a)fn?1?(a)fn?2?(a)?fn?(b)fn?1?(b)fn?2?(b)?fn?(c)fn?1?(c)fn?2?(c)????=???fn+1?(a)fn?(a)fn?1?(a)?fn+1?(b)fn?(b)fn?1?(b)?fn+1?(c)fn?(c)fn?1?(c)????
所以可以得出:
(
1
1
1
1
0
0
0
1
0
)
n
?
3
(
0
0
1
0
1
0
1
0
0
)
=
(
f
n
(
a
)
f
n
(
b
)
f
n
(
c
)
f
n
?
1
(
a
)
f
n
?
1
(
b
)
f
n
?
1
(
c
)
f
n
?
2
(
a
)
f
n
?
2
(
b
)
f
n
?
2
(
c
)
)
\begin{pmatrix} 1&1&1\\ 1&0&0\\ 0&1&0\\ \end{pmatrix}^{n-3} \begin{pmatrix} 0&0&1\\ 0&1&0\\ 1&0&0\\ \end{pmatrix} = \begin{pmatrix} f_n(a)&f_n(b)&f_n(c)\\ f_{n-1}(a)&f_{n-1}(b)&f_{n-1}(c)\\ f_{n-2}(a)&f_{n-2}(b)&f_{n-2}(c)\\ \end{pmatrix}
???110?101?100????n?3???001?010?100????=???fn?(a)fn?1?(a)fn?2?(a)?fn?(b)fn?1?(b)fn?2?(b)?fn?(c)fn?1?(c)fn?2?(c)???? - 第二步,算出那个
f
x
=
c
d
×
o
t
h
e
r
s
f_x=c^d\times others
fx?=cd×others 底数为
c
c
c 的指数是多少,相同的道理,写出转移矩阵
(
1
1
1
1
1
?
2
1
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
1
)
×
(
c
i
c
i
?
1
c
i
?
2
2
i
2
)
=
(
c
i
+
1
c
i
c
i
?
1
2
(
i
+
1
)
2
)
\begin{pmatrix} 1&1&1&1&1&-2\\ 1&0&0&0&0&0\\ 0&1&0&0&0&0\\ 0&0&0&0&1&1\\ 0&0&0&0&0&1\\ \end{pmatrix} \times \begin{pmatrix} c_i\\ c_{i-1}\\ c_{i-2}\\ 2i\\ 2 \end{pmatrix} = \begin{pmatrix} c_{i+1}\\ c_{i}\\ c_{i-1}\\ 2(i+1)\\ 2 \end{pmatrix}
???????11000?10100?10000?10000?10010??20011????????×???????ci?ci?1?ci?2?2i2????????=???????ci+1?ci?ci?1?2(i+1)2????????
所以我们有:
(
1
1
1
1
1
?
2
1
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
1
)
n
?
4
×
(
14
6
2
12
2
)
=
(
c
n
+
2
c
n
+
1
c
n
2
(
n
+
2
)
2
)
\begin{pmatrix} 1&1&1&1&1&-2\\ 1&0&0&0&0&0\\ 0&1&0&0&0&0\\ 0&0&0&0&1&1\\ 0&0&0&0&0&1\\ \end{pmatrix}^{n-4} \times \begin{pmatrix} 14\\ 6\\ 2\\ 12\\ 2 \end{pmatrix} = \begin{pmatrix} c_{n+2}\\ c_{n+1}\\ c_{n}\\ 2(n+2)\\ 2 \end{pmatrix}
???????11000?10100?10000?10000?10010??20011????????n?4×???????1462122????????=???????cn+2?cn+1?cn?2(n+2)2???????? - 还有一点注意的,由于这里的数字都是指数,根据欧拉降幂,需要取模
φ
(
P
)
=
P
?
1
\varphi(P)=P-1
φ(P)=P?1
代码
- 时间复杂度:
O
(
s
z
3
×
log
?
n
)
O(sz^3\times \log n)
O(sz3×logn)
#include<bits/stdc++.h>
using namespace std;
void show(){std::cerr << endl;}template<typename T,typename... Args>void show(T x,Args... args){std::cerr << "[ " << x << " ] , ";show(args...);}
#define ll long long
const int MAX = 3e2+50;
const int MOD = 1e9+6;
const int MOD2 = 1e9+7;
typedef long long Elemtype;
const int SZ = 5;
struct Matrix{
Elemtype mat[SZ][SZ];
}M1,M2,M3,M0;
Matrix mul(Matrix x,Matrix y,ll sz){
Matrix ans;
for(int i=0;i<sz;++i){
for(int j=0;j<sz;++j){
ans.mat[i][j]=0;
for(int k=0;k<sz;++k){
ans.mat[i][j]+=(x.mat[i][k]*y.mat[k][j])%MOD;
}
ans.mat[i][j]%=MOD;
}
}
return ans;
}
ll qpow(ll a, ll n,ll pmod)
{
ll ans = 1;
while(n){
if(n&1){
ans=ans*a%pmod;
}
n>>=1;
a=a*a%pmod;
}
return ans;
}
Matrix Create_Matrix(ll sz){
Matrix ans;
for(ll i=0;i<sz;++i)
for(ll j=0;j<sz;++j)
if(i==j)ans.mat[i][j]=1;
else ans.mat[i][j]=0;
return ans;
}
Matrix M_qpow(Matrix x,ll n,ll sz)
{
Matrix ans = Create_Matrix(sz);
while(n){
if(n&1){
ans = mul(ans,x,sz);
}
n>>=1;
x = mul(x,x,sz);
}
return ans;
}
void show_M(Matrix x,int sz){
puts("---");
for(int i = 0;i < sz;++i){
for(int j = 0;j < sz;++j){
cout << x.mat[i][j] << " ";
}
puts("");
}
puts("---");
}
int main()
{
ll n,a,b,c,d;
ll ans = 0;
cin >> n >> a >> b >> c >> d;
M1.mat[0][0] = M1.mat[0][1] = M1.mat[0][2] = 1;
M1.mat[1][0] = M1.mat[2][1] = 1;
M1 = M_qpow(M1,n-3,3);
M0.mat[0][2] = M0.mat[1][1] = M0.mat[2][0] = 1;
M1 = mul(M1,M0,3);
ans = qpow(a,M1.mat[0][0],MOD2) * qpow(b,M1.mat[0][1],MOD2) % MOD2 * qpow(c,M1.mat[0][2],MOD2) % MOD2;
M2.mat[0][0] = M2.mat[0][1] = M2.mat[0][2] = M2.mat[0][3] = 1;
M2.mat[0][4] = (-2 + MOD);
M2.mat[1][0] = M2.mat[2][1] = M2.mat[3][3] = M2.mat[3][4] = M2.mat[4][4] = 1;
M2 = M_qpow(M2,n-4,5);
M3.mat[0][0] = 14;
M3.mat[1][0] = 6;
M3.mat[2][0] = 2;
M3.mat[3][0] = 12;
M3.mat[4][0] = 2;
M3 = mul(M2,M3,5);
ans = ans * qpow(d,M3.mat[2][0],MOD2) % MOD2;
printf("%lld",ans);
return 0;
}
E:Divisibility Rules | CF180B
题意
思路
- 前置:
?
\color{red}{*}
?
x
n
?
1
=
(
x
?
1
)
(
x
n
?
1
+
x
n
?
2
+
?
+
1
)
x^n-1=(x-1)(x^{n-1}+x^{n-2}+\cdots+1)
xn?1=(x?1)(xn?1+xn?2+?+1)
?
\color{red}{*}
?
x
n
+
1
=
(
x
+
1
)
(
x
n
?
1
?
x
n
?
2
+
?
+
1
)
x^n+1=(x+1)(x^{n-1}-x^{n-2}+\cdots+1)
xn+1=(x+1)(xn?1?xn?2+?+1) 其中
n
n
n 是奇数 - 首先是最简单的
2
?
t
y
p
e
2-type
2?type
注意到,也就是我们希望满足
d
×
k
=
b
x
d\times k=b^x
d×k=bx 对于最小的正整数
x
x
x 和一个正整数
k
k
k 成立。
注意到,此时
d
d
d 的所有质因子都必须包含于
b
b
b 的所有质因子。
代码实现上,若
gcd
?
(
d
,
b
)
≠
1
\gcd(d,b)\ne 1
gcd(d,b)?=1,则我们每次让
d
=
d
/
gcd
?
(
d
,
b
)
d=d/\gcd(d,b)
d=d/gcd(d,b),没除一次,则
x
=
x
+
1
x=x+1
x=x+1
此时若
d
=
1
d=1
d=1,则就是
2
?
t
y
p
e
2-type
2?type,此时的
x
x
x 就是最小的
x
x
x - 然后就是
3
,
11
,
6
?
t
y
p
e
3,11,6-type
3,11,6?type
看
3
?
t
y
p
e
3-type
3?type,我们需要把
b
b
b 进制下的
d
d
d 写出来。
d
=
∑
i
=
0
∞
a
i
b
i
d=\sum_{i=0}^\infin a_ib^i
d=i=0∑∞?ai?bi
注意到此时我们当然有
∑
i
=
0
∞
a
i
b
i
≡
0
(
m
o
d
d
)
\sum_{i=0}^\infin a_ib^i \equiv 0\pmod d
i=0∑∞?ai?bi≡0(modd)
对于
3
?
t
y
p
e
3-type
3?type,我们有
∑
i
=
0
∞
a
i
≡
0
(
m
o
d
d
)
\sum_{i=0}^\infin a_i \equiv 0\pmod d
i=0∑∞?ai?≡0(modd)
两式子合并,得到:
∑
i
=
0
∞
a
i
(
b
i
?
1
)
≡
0
(
m
o
d
d
)
∑
i
=
0
∞
a
i
(
b
?
1
)
(
o
t
h
e
r
s
)
≡
0
(
m
o
d
d
)
\sum_{i=0}^\infin a_i(b^i-1) \equiv 0\pmod d\\ \sum_{i=0}^\infin a_i(b-1)(others) \equiv 0\pmod d\\
i=0∑∞?ai?(bi?1)≡0(modd)i=0∑∞?ai?(b?1)(others)≡0(modd)
也就是说
b
?
1
b-1
b?1 是
d
d
d 的倍数 - 然后是
11
?
t
y
p
e
11-type
11?type,同理
∑
i
=
0
∞
a
i
b
i
≡
0
(
m
o
d
d
)
∑
i
=
0
∞
(
?
1
)
i
+
1
a
i
≡
0
(
m
o
d
d
)
\sum_{i=0}^\infin a_ib^i \equiv 0\pmod d\\ \sum_{i=0}^\infin (-1)^{i+1}a_i\equiv 0\pmod d
i=0∑∞?ai?bi≡0(modd)i=0∑∞?(?1)i+1ai?≡0(modd)
得到以下式子:
∑
i
=
0
∞
a
i
(
b
i
+
(
?
1
)
i
+
1
)
≡
0
(
m
o
d
d
)
\sum_{i=0}^\infin a_i(b^i+(-1)^{i+1}) \equiv 0\pmod d\\
i=0∑∞?ai?(bi+(?1)i+1)≡0(modd)
若
i
i
i 是奇数,则会变成
b
J
+
1
=
(
b
+
1
)
(
O
t
h
e
r
s
)
b^J+1=(b+1)(Others)
bJ+1=(b+1)(Others) 的形式
若
i
i
i 是偶数,则会变成
b
2
x
?
1
=
(
b
x
+
1
)
(
b
x
?
1
)
b^{2x}-1=(b^x+1)(b^x-1)
b2x?1=(bx+1)(bx?1) 若
x
x
x 是奇数,那么左边这一项可以分出来一个
(
b
+
1
)
(
O
t
h
e
r
s
)
(b+1)(Others)
(b+1)(Others);若
x
x
x 是偶数,那么继续拆
b
x
?
1
b^x-1
bx?1,就是一个递归问题了。 - 所以此时一定有
1
+
b
1+b
1+b 是
d
d
d 的倍数
注意,以上两种都要求
x
=
0
x=0
x=0,也就是
gcd
?
(
b
,
d
)
=
1
\gcd(b,d)=1
gcd(b,d)=1
6
?
t
y
p
e
6-type
6?type,也就是上述有两种同时满足,就是
b
+
1
和
b
?
1
b+1和 b-1
b+1和b?1 同时是
d
d
d 的倍数即可。
?
\color{red}{*}
? 如果符合
3
?
t
y
p
e
3-type
3?type 或者
11
?
t
y
p
e
11-type
11?type,那么一定符合
2
?
t
y
p
e
2-type
2?type
否则就是
7
?
t
y
p
e
7-type
7?type
代码
- 时间复杂度:
O
(
log
?
R
)
O(\log R)
O(logR)
#include<bits/stdc++.h>
using namespace std;
void show(){std::cerr << endl;}template<typename T,typename... Args>void show(T x,Args... args){std::cerr << "[ " << x << " ] , ";show(args...);}
#define ll long long
const int MAX = 3e2+50;
const int MOD = 1e9+6;
int lcm(int x,int y){
return x * y / __gcd(x,y);
}
int main()
{
int b,d,dd,cnt = 0;
cin >> b >> d;
dd = d;
while(__gcd(dd,b) > 1){
dd /= __gcd(dd,b);
cnt++;
}
if(dd == 1){
puts("2-type");
printf("%d",cnt);
}else if(!(lcm(b-1,b+1) % dd)){
if(!cnt && !((b-1) % dd))puts("3-type");
else if(!cnt && !((b+1) % dd))puts("11-type");
else puts("6-type");
}else{
puts("7-type");
}
return 0;
}
|


