[数据结构与算法]浙大MOOC《数据结构》第8题——Tree Traversals Again

题目链接
讲解链接（陈越姥姥yyds）
题目图片

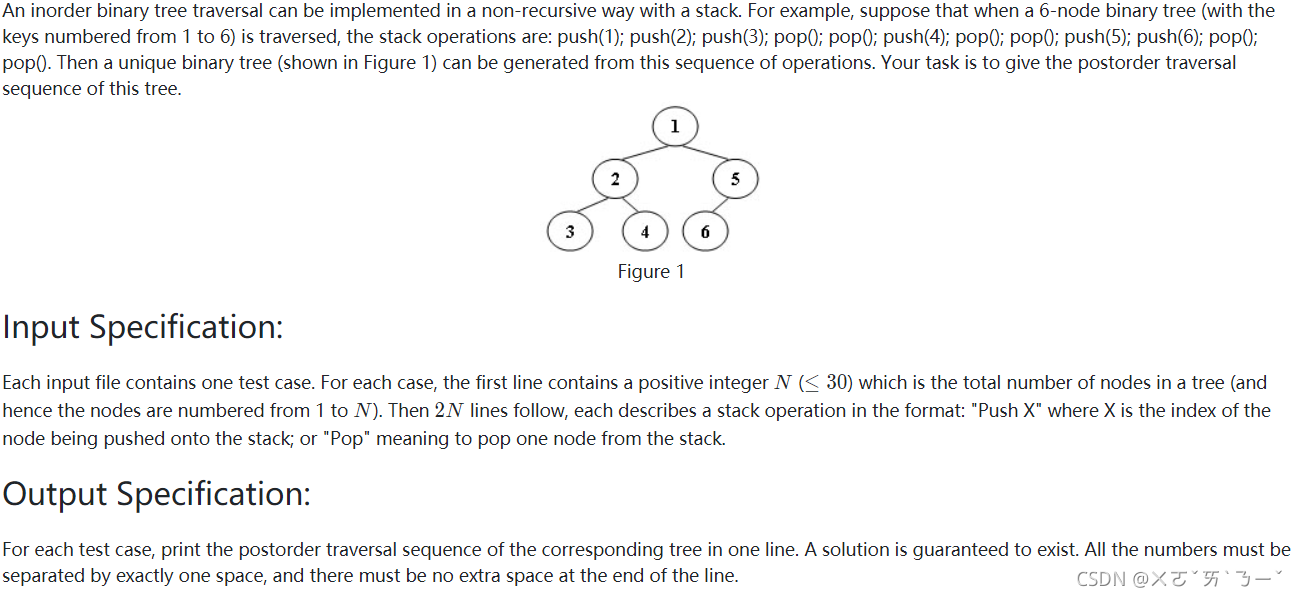
输入输出示例

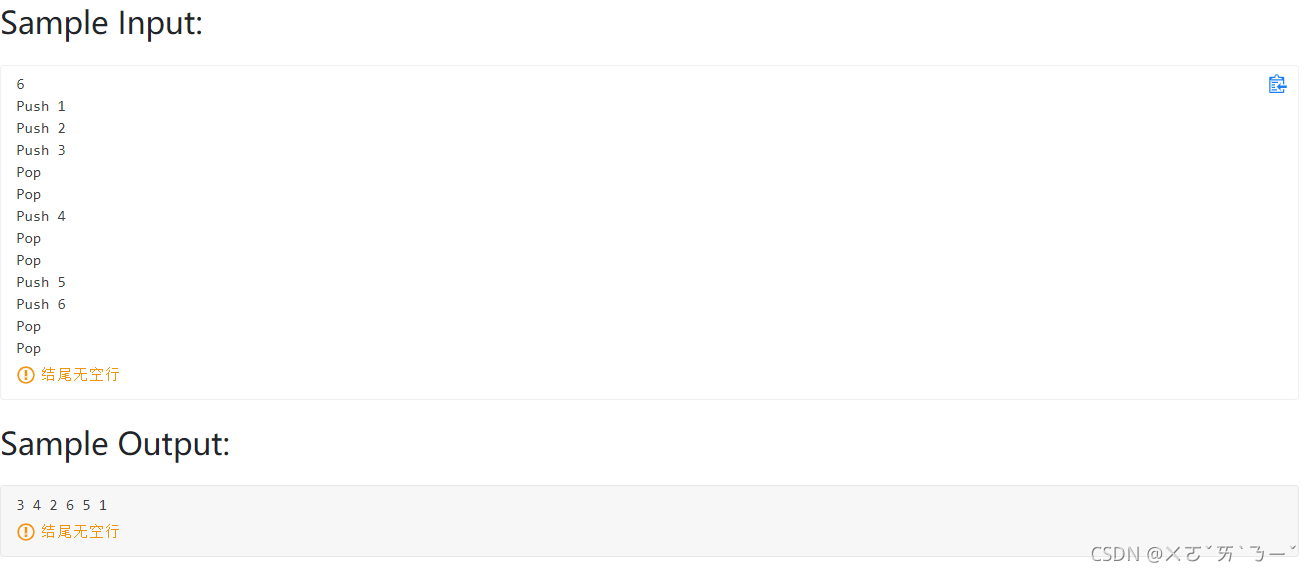
思路：
将树画出来，

将压栈、入栈操作分别列出

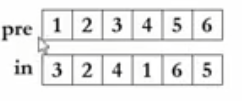
有没有发现，其实压栈顺序就是先序遍历顺序，而出栈顺序则是中序遍历顺序！！！，中序遍历操作，pop顺序就是中序遍历顺序，不难理解，那为啥push顺序刚好是先序遍历捏？
因为为我们每次遇到一个节点都需要先保存下来（即压栈），然后再去找左子树，这样在弹出栈时才能让左子树先弹，达到先序遍历的效果。
所以我们就这样得到了树的pre、in顺序的遍历。
那么，怎样仅用这两个顺序就得到后序遍历呢？
首先，我们要明确，先序遍历时数字肯定是按照
根节点 | 左子树元素 | 右子树元素的顺序排列的

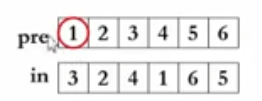
现在根节点已经确定了，怎样分开pre数组中左子树和右子树元素呢？
这就要用到in数组了

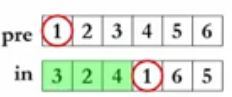
发现没有？in里面根节点左边3个就是左子树元素，右边两个就是右子树元素

现在，既然我们有了将pre 和in数组里根节点、左子树、右子树分开的办法，那我们是不是就可以递归的在in数组里找右子树并打印出来呢？
下面给出建树的办法，来自大佬余-cos的代码

#include <iostream>
#include <string>
#include <queue>
#include <stack>
typedef int Tree;
using namespace std;
#define maxsize 35
#define Null -1
int N,x;
int cnt=0;
typedef int tree;
struct TNode{
    int data;
    tree left,right;
}T1[maxsize];
stack<char> s;
int c2i(char ch){
    return ch-'0';
}
Tree Rebuild(string preod,string inod)
{
    Tree R;//当前树的根节点
    if(preod.empty()&&inod.empty())return Null;
    R=c2i(preod[0]);;
    int l,r,Rindex,len;//左子树大小，右子树大小，根节点位置，当前树长度
    len=preod.length();
    Rindex=inod.find(preod[0],0);
    l=Rindex;
    r=len-1-Rindex;
    if(Rindex!=0)
    {
        T1[R].left=Rebuild(preod.substr(1,l),inod.substr(0,l));
    }
    else
    {
        T1[R].left=Null;
    }
    if(Rindex!=len-1)
    {
        T1[R].right=Rebuild(preod.substr(Rindex+1,r),inod.substr(Rindex+1,r));
    }
    else
    {
        T1[R].right=Null;
    }
    return R;
}
void PostOrderTraversal(Tree R)
{
    if(R==Null)return;
    PostOrderTraversal(T1[R].left);
    PostOrderTraversal(T1[R].right);
    if(cnt==0)cout<<R;
    else cout<<" "<<R;
    cnt++;
}
string o;
int main()
{
    string preod,inod;
    char ch;
    cin>>N;
    getchar();
    int n=2*N;
    for(int i=0;i<n;++i)
    {
        cin>>o;
        if(o=="Push"){
            cin>>x;
            ch=x+'0';
            s.push(ch);
            preod+=ch;
        }else{
            inod+=s.top();
            s.pop();
        }
        getchar();
    }
    Tree R1;
    R1=Rebuild(preod,inod);
    PostOrderTraversal(R1);
    //cout<<endl;
    system("pause");
    return 0;
}

接下来是不建树的办法

#include <iostream>
#include <vector>
#include <string>
#include <stack>
#include <algorithm>
using namespace std;
int N,cnt=0;
void posttravel(vector<int>&in,vector<int>&pre,int R,int rear,int R_in,int rear_in)
{
    int root=R;
    int i;
    if(root>rear)return;
    if(root==rear)
    {
        cout<<pre[root];
        cnt++;
        if(cnt!=N)
        cout<<" ";
        return;
    }
    for ( i = R_in; i <= rear_in; i++)
    {
        if(in[i]==pre[root])
        {
            break;//i为in中根节点位置
        }
    }
    posttravel(in,pre,root+1,root+i-R_in,R_in,i-1);
    posttravel(in,pre,root+i-R_in+1,rear,i+1,rear_in);
    cout<<pre[root];
    cnt++;
    if(cnt!=N)
    cout<<" ";
    return;
}
int main()
{
    int n;
    string oper;
    cin>>n;
    int tmp;
    vector<int> in;
    vector<int> pre;
    stack <int> s;
    for(int i=0;i<n*2;i++)
    {
        cin>>oper;
        if(oper=="Push")
        {
            cin>>tmp;
            pre.push_back(tmp);
            s.push(tmp);
        }
        else
        {
            in.push_back(s.top());
            s.pop();
        }
    }
    N=in.size();
    posttravel(in,pre,0,pre.size()-1,0,in.size()-1);
    //system("pause");//用于查看测试结果
    return 0;
}

两种版本代码皆可通过所有测试用例
P.S 对数组边界不够敏感，还得多练习啊T_T