概述
-
排序:将无序序列转换成一个有序序列的运算(由小到大或由大到小)
如果参加排序的数据结点包含多个数据域,那么排序往往是针对其中某个域而言
-
排序的分类
-
按主要操作:比较排序、基数排序
- 比较排序:用比较的方法进行排序,包括插入排序、交换排序、选择排序、归并排序
- 基数排序:不用比较的方法,仅根据元素自身值的特点直接排序
-
按辅助空间:原地排序、非原地排序
- 原地排序:空间复杂度为 O ( 1 ) O(1) O(1)的排序,包括各种简单排序和堆排序
- 非原地排序:空间复杂度大于 O ( 1 ) O(1) O(1)的排序,包括堆排序、
-
按稳定性:稳定排序、非稳定排序
-
稳定排序:值相等的结点排序后相对次序一定不变
-
非稳定排序:值相等的结点排序后相对次序可能改变
排序的稳定性只对结构型数据有意义,比如学生成绩,先按数学成绩排序,再按总分排序,如果排序是稳定的,那么在总分相同的情况下,数学成绩高的会在前面
-
-
按自然性:自然排序、非自然排序
- 自然排序:数据越有序,排序时间越短
- 非自然排序:不满足上述条件的排序
-
按数据存储介质:内部排序、外部排序
-
内部排序:数据量不大,数据全部在内存中直接进行排序
-
外部排序:数据量较大,数据需要分批从外存中调入内存进行排序,排序的中间结果也需要调出到外存
-
-
按比较器个数:串行排序、并行排序
- 串行排序:单处理机,同一时刻比较一对数据
- 并行排序:多处理机,同一时刻比较多对数据
-
-
本章研究的内容
-
研究的排序限于内部排序、串行排序
-
按主要操作
- 插入排序:直接插入排序、二分插入排序、希尔排序
- 交换排序:冒泡排序、快速排序
- 选择排序:简单选择排序、堆排序
- 归并排序:2-路归并排序
- 基数排序
-
排序的时间复杂度
- 简单的排序方法(直接插入排序、冒泡排序、简单选择排序): O ( n 2 ) O(n^2) O(n2)
- 先进的排序方法(快速排序、堆排序): O ( n l o g n ) O(nlogn) O(nlogn)
- 基数排序: O ( n ) O(n) O(n)
-
记录序列的存储结构:顺序表
#include<stdio.h> #define MAXSIZE 20 // 设记录不超过20个 // 假设排序的关键字为整型 typedef int KeyType; // 定义每个记录的结构类型 /* typedef struct { KeyType key; // 关键字 InfoType otherinfo; // 其他数据信息 }RecordType; */ /** * 由于要研究的问题是排序,是对于关键字的排序,与记录中的其他信息无关 * 因此我们就直接将其他信息先抹去,单独研究对关键字的排序 * 直接定义记录就是整型量 */ typedef int RecordType; // 定义顺序表 typedef struct { RecordType elem[MAXSIZE+1]; // 定义数组,多设一格,0号位置为哨兵或缓冲区 int length; // 顺序表的长度 }SqList; // 将数组转换成顺序表 SqList CreateList(RecordType array[], int length) { SqList L; for(int i = 1; i <= length && i <= MAXSIZE; i++, L.length++) L.elem[i] = array[i-1]; return L; } // 展示顺序表 void ShowList(SqList L) { if(L.length) { // 非空表的情况 printf("["); for(int i = 1; i <= L.length-1; i++) // 最后一位单独输出 printf("%d, ", L.elem[i]); printf("%d]\n", L.elem[L.length]); // 最后一位单独输出 } else printf("[]\n"); // 空表的情况 }
-
插入排序
-
基本思想
从头开始依次拿出一个待排序的结点,按其关键字大小,插入到前面已经排好序的序列的适当位置上,直到遍历完所有结点为止。即边插入边排序,保证子序列随时都是有序的
直接插入排序
-
基本思想:采用顺序查找法的插入排序

-
算法实现
#include<stdio.h> #include"SqListForSort.h" void InsertSort(SqList *L) { int i, j; for(i = 2; i <= L->length; i++) // i遍历待插入结点,从第2个结点开始 // 先排除非常情况:如果待插入结点比前驱都大,说明已经有序了,那就根本不需要动 // 只有待插入结点比前驱小的情况下才需要向前寻找插入位置 if(L->elem[i] < L->elem[i-1]) { L->elem[0] = L->elem[i]; // 赋值给哨兵 // j向前遍历寻找插入位置,当待插入结点大于等于当前结点时,当前结点的后继就是插入位置 // 即使待插入结点特别小,最多也只会插入在哨兵后面,不会超出范围 for(j = i-1; L->elem[0] < L->elem[j]; j--) L->elem[j+1] = L->elem[j]; // 如果待插入结点小于当前结点,就把当前结点后移 L->elem[j+1] = L->elem[0]; // 插入到当前结点的后继 } } int main() { KeyType array[] = {10, 3, 5, 16, 7, 32, 83, 23, 7, 54, 29, 96}; SqList L = CreateList(array, 11); ShowList(L); InsertSort(&L); ShowList(L); return 0; } -
算法分析
-
时间性能
-
最好情况(正序):比较次数是n-1次,移动次数是0次
-
最坏情况(逆序)
比较次数是 ∑ i = 2 n i = ( n + 2 ) ( n ? 1 ) 2 \sum_{i = 2}^n i = \frac{(n+2)(n-1)}{2} ∑i=2n?i=2(n+2)(n?1)?次,移动次数是 ∑ i = 2 n i + 1 = ( n + 4 ) ( n ? 1 ) 2 \sum_{i = 2}^n {i+1} = \frac{(n+4)(n-1)}{2} ∑i=2n?i+1=2(n+4)(n?1)?次
-
最坏情况和平均情况时间复杂度都是 O ( n 2 ) O(n^2) O(n2),最好情况为 O ( n ) O(n) O(n)
-
原始数据越接近有序,排序速度越快,因此直接插入排序是自然排序
-
-
空间性能:空间复杂度 O ( 1 ) O(1) O(1)
-
稳定性:稳定
-
二分插入排序
-
基本思想:采用二分查找法的插入排序
-
算法实现
#include<stdio.h> #include"SqListForSort.h" void BInsertSort(SqList *L) { int i, j, low, high, mid; for(i = 2; i <= L->length; i++) // i遍历待插入结点,从第2个结点开始 // 先排除非常情况:如果待插入结点比前驱大或者相等,说明已经有序了,根本不需要动 // 如果待插入结点比前驱小,说明逆序了,这时候就需要调整 if(L->elem[i] < L->elem[i-1]) { L->elem[0] = L->elem[i]; // 赋值给哨兵 // 直接插入排序在查找插入位置时采用顺序查找法 // 既然前面已经是有序的,我们可以改进查找方式为二分查找法 low = 1, high = i-1; while(low <= high) { // 当high在low的左边时才出循环 mid = (low+high)/2; if(L->elem[0] < L->elem[mid]) high = mid - 1; // 如果待插入结点小于中间结点,就从左半边找 else low = mid + 1; // 如果待插入结点大于中间结点,就从右半边找 } // 出循环后,high+1的位置就是插入的位置 for(j = i; j-1 >= high+1; j--) // 记录后移 L->elem[j] = L->elem[j-1]; L->elem[high+1] = L->elem[0]; } } int main() { KeyType array[] = {10, 3, 5, 16, 7, 32, 83, 23, 7, 54, 29, 96}; SqList L = CreateList(array, 11); ShowList(L); BInsertSort(&L); ShowList(L); return 0; } -
算法分析
- 时间性能
- 二分插入排序减少了比较次数,但没有减少移动次数
- 平均性能优于直接插入排序
- 时间复杂度 O ( n 2 ) O(n^2) O(n2)
- 空间性能:空间复杂度 O ( 1 ) O(1) O(1)
- 稳定性:稳定
- 不适合在链式存储结构上实现
- 时间性能
希尔排序
-
基本思想
利用了直接插入排序在个数较少、基本有序的情况下效率更高的特点
先将整个待排记录序列分割成若干子序列,分别进行直接插入排序,待整个序列中的记录“基本有序”时,再对全体记录进行一次直接插入排序。
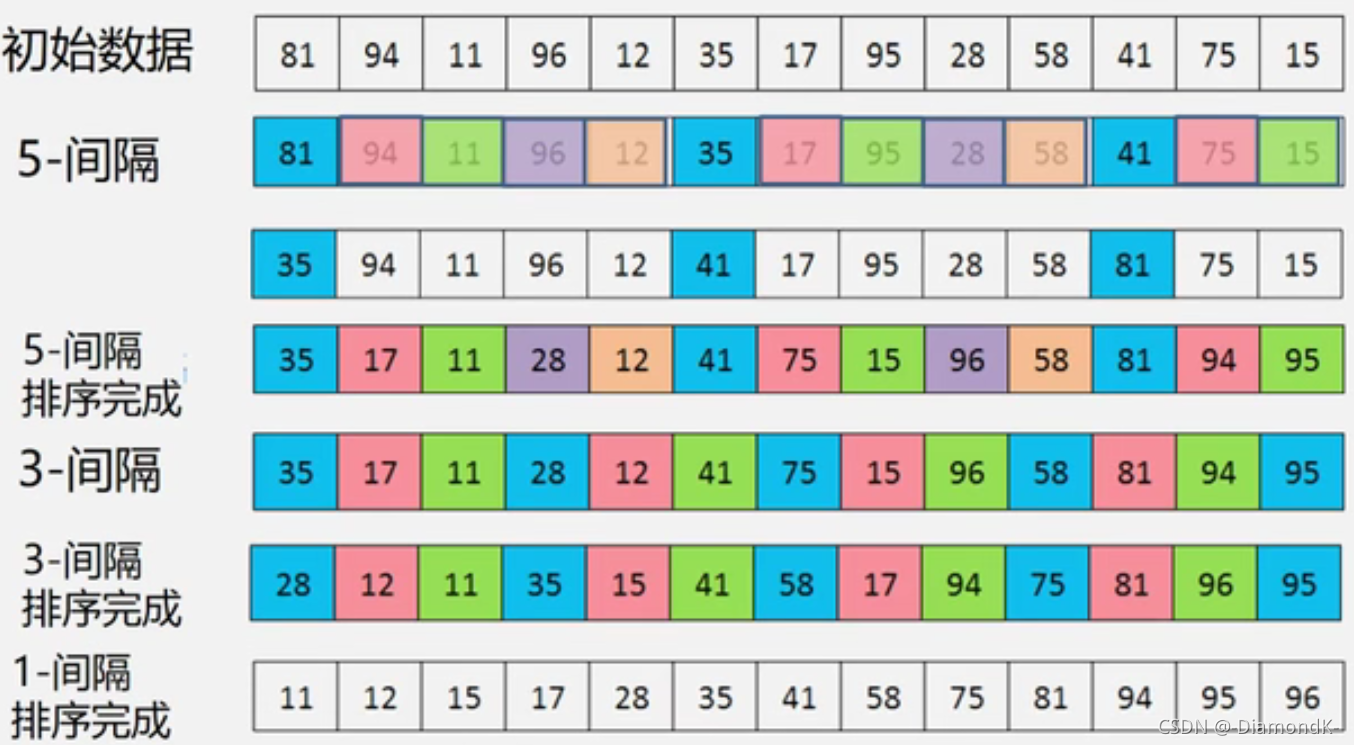
- 一次移动,移动位置较大,跳跃式地接近排序后的最终位置,最后一次只需要少量移动
- 增量序列必须是递减的,最后一个必须是1;增量序列应该是互质的
-
算法实现
#include<stdio.h> #include"SqListForSort.h" // 对于每个增量进行直接插入排序 void ShellInsert(SqList *L, int dk) { int n, i, j; for(n = 1; n <= dk; n++) // n控制增量的开始位置(比如增量为5时,先从1,6,11;再2,7,12) for(i = n; i <= L->length; i = i+dk) // i遍历待插入结点,从第n个结点开始,增量为dk // 先排除非常情况:如果待插入结点比“前驱”都大,说明已经有序了,根本不需要动 // 如果待插入结点比“前驱”小,说明逆序了,这时候就需要调整 if(L->elem[i] < L->elem[i-dk]) { L->elem[0] = L->elem[i]; // 赋值给哨兵 // j向前遍历寻找插入位置,当待插入结点大于等于当前结点时,当前结点的“后继”就是插入位置 // 当增量不为1时,哨兵失去作用,需要加一层判断,防止越界 for(j = i-dk; L->elem[0] < L->elem[j] && j >= n; j = j-dk) L->elem[j+dk] = L->elem[j]; // 如果待插入结点小于当前结点,就把当前结点后移 L->elem[j+dk] = L->elem[0]; // 插入到当前结点的“后继” } } // 希尔排序主函数 // dlta[]中保存增量dk的值,称为增量序列,增量序列是递减的,互质的,且最后一位为1 // t给出增量序列的长度 void ShellSort(SqList *L, int dlta[], int t) { for(int k = 0; k <= t-1; k++) ShellInsert(L, dlta[k]); } int main() { KeyType array[] = {10, 3, 5, 16, 7, 32, 83, 23, 7, 54, 29, 96}; int dlta[] = {5, 3, 1}; SqList L = CreateList(array, 11); ShowList(L); ShellSort(&L, dlta, 3); ShowList(L); return 0; } -
算法分析
- 时间性能:时间复杂度是n和d的函数,根据经验介于 O ( n 1.25 ) O(n^{1.25}) O(n1.25)~ O ( 1.6 n 1.25 ) O(1.6n^{1.25}) O(1.6n1.25)之间
- 空间性能:空间复杂度 O ( 1 ) O(1) O(1)
- 稳定性:稳定
- 不适合在链式存储结构上实现
交换排序
- 基本思想:两两比较,如果发逆序则交换,直到所有记录都排好序为止
冒泡排序
-
基本思想:按顺序两两比较,逆序则交换

-
算法实现
#include<stdio.h> #include"SqListForSort.h" void BubbleSort(SqList *L) { int i, j, flag; // flag判断每次冒泡是否有进行交换 for(i = L->length, flag = 0; i >= 2; i--) { // i控制冒泡的结束位置 if(flag) return; // 如果没有进行交换则说明已经有序,可以直接退出 for(j = 1, flag = 1; j+1 <= i; j++) // j控制两两比较冒泡 if(L->elem[j] > L->elem[j+1]) { // 逆序则交换 flag = 0; L->elem[0] = L->elem[j]; L->elem[j] = L->elem[j+1]; L->elem[j+1] = L->elem[0]; } } } int main() { KeyType array[] = {10, 3, 5, 16, 7, 32, 83, 23, 7, 54, 29, 96}; SqList L = CreateList(array, 11); ShowList(L); BubbleSort(&L); ShowList(L); return 0; } -
算法分析
-
时间性能
-
最好情况(正序):比较次数是n-1次,移动次数是0次
-
最坏情况(逆序)
比较次数是 ∑ i = 1 n ? 1 n ? i = 1 2 ( n 2 ? n ) \sum_{i = 1}^{n-1}{n-i} = \frac{1}{2}(n^2-n) ∑i=1n?1?n?i=21?(n2?n)次,移动次数 3 ∑ i = 1 n ? 1 n ? i = 3 2 ( n 2 ? n ) 3\sum_{i = 1}^{n-1}{n-i} = \frac{3}{2}(n^2-n) 3∑i=1n?1?n?i=23?(n2?n)
-
最坏情况和平均情况时间复杂度都是 O ( n 2 ) O(n^2) O(n2),最好情况为 O ( n ) O(n) O(n)
-
原始数据越接近有序,排序速度越快,因此冒泡排序是自然排序
-
-
空间性能:空间复杂度 O ( 1 ) O(1) O(1)
-
稳定性:稳定
-
快速排序
-
基本思想
任取一个元素为中心,所有比它小的元素一律前放,比它大的元素一律后放,形成左右两个子表;对各子表重新选择中心元素并依此规则调整(递归思想),直到每个子表的元素只剩一个

-
算法实现

#include<stdio.h> #include"SqListForSort.h" int Partition(SqList *L, int low, int high) { L->elem[0] = L->elem[low]; // 把枢轴元素赋值给哨兵 // 左右指针交替循环,把比枢轴小的元素全部放到左边,把比枢轴大或等的元素全部放到右边 while(low < high) { // high指针和low指针重合时结束循环 //high指针在右边不断左移,寻找比枢轴元素小的元素,将其放到low的位置 for(; low < high; high--) if(L->elem[high] < L->elem[0]) { L->elem[low] = L->elem[high]; break; } //low指针不断在左边右移,寻找比枢轴元素大或等的元素,将其放到high的位置 for(; low < high; low++) if(L->elem[low] >= L->elem[0]) { L->elem[high] = L->elem[low]; break; } } L->elem[low] = L->elem[0]; // low和high重合后的位置就是枢轴位置 return low; } void Qsort(SqList *L, int low, int high) { int privotloc; if(low < high) { // 子表长度为1时结束递归 privotloc = Partition(L, low, high); // 对当前子表排序并返回枢轴位置 Qsort(L, low, privotloc-1); // 对低子表进行递归排序 Qsort(L, privotloc+1, high); // 对高子表进行递归排序 } } void QuickSort(SqList *L) { Qsort(L, 1, L->length); // 给一个初始状态:low为1,high为L->length } int main() { KeyType array[] = {10, 3, 5, 16, 7, 32, 83, 23, 7, 54, 29, 96}; SqList L = CreateList(array, 11); ShowList(L); QuickSort(&L); ShowList(L); return 0; } -
算法分析
-
时间性能
- 时间复杂度 O ( n l o g n ) O(nlogn) O(nlogn)
- 但最坏情况(逆序)下,退化为了冒泡排序,时间复杂度为 O ( n 2 ) O(n^2) O(n2)
- 快速排序适于对原本有序或基本有序的记录序列进行排序
- 快速排序不是自然排序
-
空间性能
快速排序不是原地排序,因为快速排序用了递归,需要递归调用栈的支持,栈的长度取决于递归调用的深度。即使不用递归,也需要用户栈
-
在平均情况下:需要 O ( l o g n ) O(logn) O(logn)的栈空间
-
最坏情况下:栈空间可达 O ( n ) O(n) O(n)
-
-
稳定性:不稳定
-
选择排序
简单选择排序
-
基本思想:在待排序的数据中选出最大(小)的元素放在其最终的位置

-
算法实现
#include<stdio.h> #include"SqListForSort.h" void SelectSort(SqList *L) { int i, j, minloc; for(i = 1; i <= L->length-1; i++) { // i控制选择起点 for(j = i, minloc = i; j <= L->length; j++) // j遍历元素寻找最小值的位置 if(L->elem[j] < L->elem[minloc]) minloc = j; L->elem[0] = L->elem[i]; // 将最小值与选择起点的元素交换 L->elem[i] = L->elem[minloc]; L->elem[minloc] = L->elem[0]; } } int main() { KeyType array[] = {10, 3, 5, 16, 7, 32, 83, 23, 7, 54, 29, 96}; SqList L = CreateList(array, 11); ShowList(L); SelectSort(&L); ShowList(L); return 0; } -
算法分析
- 时间性能
- 最好情况(正序)移动次数为0,最坏情况(逆序)移动次数为3(n-1)
- 不管序列如何,比较次数都一样,都为 ∑ i = 1 n ? 1 ( n ? i ) = n 2 ( n ? 1 ) \sum_{i = 1}^{n-1}{(n-i)} = \frac{n}{2}(n-1) ∑i=1n?1?(n?i)=2n?(n?1)
- 时间复杂度 O ( n 2 ) O(n^2) O(n2)
- 空间性能:空间复杂度 O ( 1 ) O(1) O(1)
- 稳定性:不稳定
- 时间性能
堆排序
-
基本思想
-
堆的定义
若n个元素的序列满足 { a 1 , a 2 , . . . , a n } \{a_1, a_2, ..., a_n\} {a1?,a2?,...,an?}满足:
{ a i ≤ a 2 i a i ≤ a 2 i + 1 或 { a i ≥ a 2 i a i ≥ a 2 i + 1 \begin{cases} a_i \le a_{2i} \\ a_i \le a_{2i+1} \end{cases} 或 \begin{cases} a_i \ge a_{2i} \\ a_i \ge a_{2i+1} \end{cases} {ai?≤a2i?ai?≤a2i+1??或{ai?≥a2i?ai?≥a2i+1??
? 则分别称该序列 { a 1 , a 2 , . . . , a n } \{a_1, a_2, ..., a_n\} {a1?,a2?,...,an?}为小根堆和大根堆
? 从堆的定义可以看出,堆实质是满足如下性质的完全二叉树:二叉树中任一非叶子结点均小于/大于它的孩子结点
-
堆排序
若在输出堆顶的最小值(最大值)后,使得剩余n-1个元素的序列重又建成一个堆,则得到n个元素的次小值(次大值)……如此反复,便能得到一个有序序列,这个过程称之为堆排序
-
堆的调整
- 输出堆顶元素之后,以堆中最后一个元素替代之;
- 然后将根结点值与左、右子树的根结点值进行比较,并与其中小进行交换;
- 重复上述操作,直至叶子结点

-
-
算法实现
-
算法分析
- 时间性能:时间复杂度 O ( n l o g n ) O(nlogn) O(nlogn)
- 空间性能:时间复杂度 O ( n ) O(n) O(n)
- 稳定性:不稳定
归并排序
-
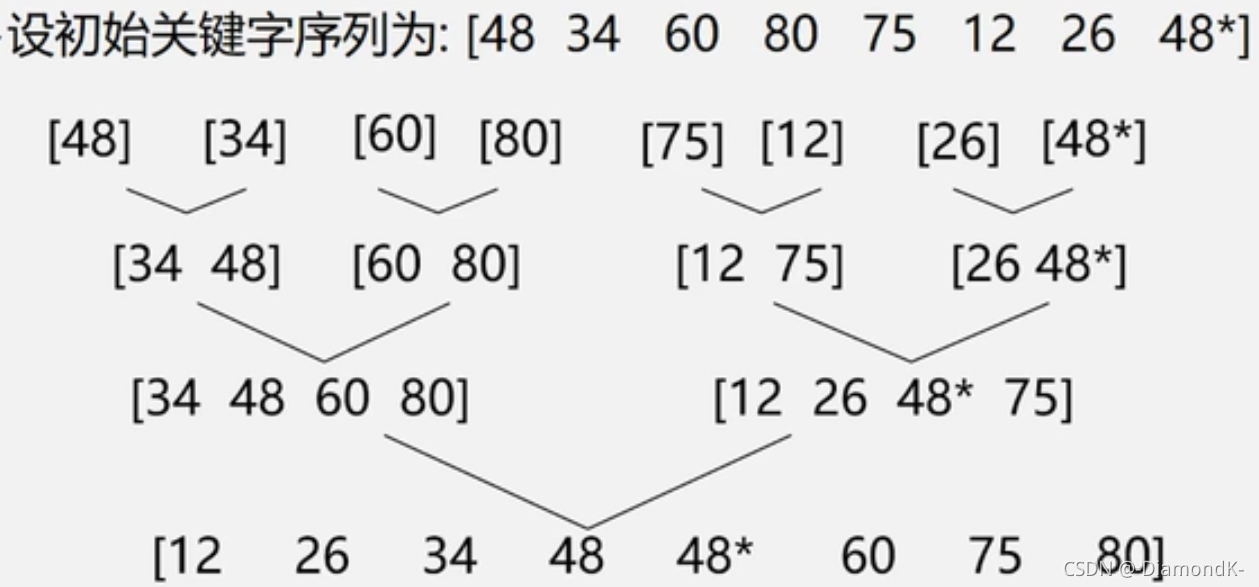
基本思想:将两个或两个以上的有序子序列归并为一个有序序列

-
算法实现
#include<stdio.h> #include"SqListForSort.h" int min(int a, int b) { return a < b ? a : b; } // 相邻有序表的合并 void Merge(SqList *L, SqList *MergeL, int low, int mid, int high) { int i, j, k; // 左有序表从low到mid,右有序表从mid+1到high i = low, j = mid + 1, k = low; while(i <= mid && j <= high) // 谁小就把谁加到MergeL中,当有一者遍历完之后停止循环 MergeL->elem[k++] = (L->elem[i] <= L->elem[j])? L->elem[i++]: L->elem[j++]; while(i <= mid) // 如果左边没遍历完,就把剩下的都加到MergeL中 MergeL->elem[k++] = L->elem[i++]; while(j <= high) // 如果右边没遍历完,就把剩下的都加到MergeL中 MergeL->elem[k++] = L->elem[j++]; } // 归并排序主函数(迭代版) void MergeSort(SqList *L) { int low, mid, high, range; SqList mergeL, *MergeL, *t; MergeL = &mergeL; MergeL->length = L->length; for(range = 1; range <= L->length; range *= 2) { // range控制子表长度 for(low = 1; low <= L->length; low += range*2) { high = min(low + range*2 - 1, L->length); mid = min(low + range - 1, L->length); Merge(L, MergeL, low, mid, high); } // 归并完成后,交换L和MergeL // 归并后的表作为下一次归并的主表 // 归并前的表作为下一次归并的辅助空间 t = L, L = MergeL, MergeL = t; } } int main() { KeyType array[] = {10, 3, 5, 16, 7, 32, 83, 23, 7, 54, 29, 96}; SqList L = CreateList(array, 11); ShowList(L); MergeSort(&L); ShowList(L); return 0; } -
算法分析
-
时间性能:时间复杂度 O ( n l o g n ) O(nlogn) O(nlogn)
-
空间性能
需要用到与原始序列同样大小的辅助序列,空间复杂度 O ( n ) O(n) O(n)
-
稳定性:稳定
-
基数排序
-
基本思想:分配+收集
按个位数字分配并收集,再按十位数字分配收集,依次进行,最后收集完成排序也完成了

-
算法实现
-
算法分析
-
时间性能:时间复杂度 O ( k ( n + m ) ) O(k(n+m)) O(k(n+m))
-
空间性能:空间复杂度 O ( n + m ) O(n+m) O(n+m)
k关键字个数(分配收集几次),m为基数个数(桶的个数)
-
稳定性:稳定
-
各种排序方法的比较
- 算法设计
- 简单排序(直接插入排序、二分插入排序、冒泡排序、简单选择排序)都是顺序遍历元素,二分排序在查找时是递归的
- 快速排序、堆排序、归并排序是递归的,采用了分治法
- 时间性能
- 根据时间复杂度分类
- O ( n ) O(n) O(n):基数排序;最快,但不是所有都能用
- O ( n l o g n ) O(nlogn) O(nlogn):快速排序、堆排序、归并排序;其中快速排序最优
- 约 O ( n 1.3 ) O(n^{1.3}) O(n1.3):希尔排序
- O ( n 2 ) O(n^2) O(n2):简单排序(直接插入排序、二分插入排序、冒泡排序、简单选择排序);二分插入排序最优
- 正序情况下
- 直接插入排序、二分插入排序和冒泡排序能达到 O ( n ) O(n) O(n),快速排序退化为 O ( n 2 ) O(n^2) O(n2)
- 其他排序时间复杂度保持不变
- 正序情况下,直接插入排序是最快的
- 根据时间复杂度分类
- 空间性能
- O ( 1 ) O(1) O(1):简单排序(直接插入排序、二分插入排序、冒泡排序、简单选择排序)、希尔排序、堆排序
- O ( l o g n ) O(logn) O(logn):快速排序
- O ( n ) O(n) O(n):归并排序、基数排序
- 稳定性
- 简单选择排序、希尔排序、快速排序、堆排序是不稳定的,其他都是稳定的