1 算法介绍

粒子群优化算法(Particle Swarm Optimization，PSO)是一种经典的群智能算法，该算法灵感源自于鸟类飞行和觅食的社会活动，鸟群通过个体之间的信息交互来寻找全局最优点。PSO算法具有原理简单、较少的参数设置和容易实现等优点，因此近年来受到学者们的广泛关注和研究。

粒子群算法模拟鸟群的捕食过程，将待优化问题看作是捕食的鸟群，解空间看作是鸟群的飞行空间，空间的每只鸟的位置即是粒子群算法在解空间的一个粒子，也就是待优化问题的一个解。

粒子群算法有以下几点假设：

粒子被假定为没有体积没有质量，本身的属性只有速度和位置。
每个粒子在解空间中运动，它通过速度改变其方向和位置。
通常粒子将追踪当前的最优粒子以经过最少代数的搜索到最优解。

在算法的进化过程中，粒子一直都跟踪两个极值：一个是到个体历史最优位置，一个是种群历史最优位置。

2 算法模型

粒子群算法的核心思想是利用群体中的个体对信息的共享，从而使整个群体的运动在问题求解空间中产生从无序到有序的演化过程，从而获得问题的最优解。

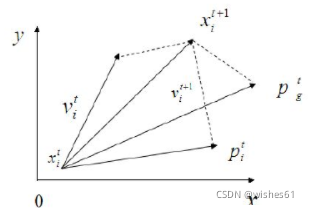
在这里插入图片描述
粒子群算法的个体位置变化按两个基本公式：

$\begin{aligned} v_{i d}^{t+1} &=\omega v_{i d}^{t}+c_{1} r_{1}\left(p_{i d}^{t}-x_{i d}^{t}\right)+c_{2} r_{2}\left(p_{g d}^{t}-x_{i d}^{t}\right) \\ x_{i d}^{t+1} &=x_{i d}^{t}+v_{i d}^{t+1} \end{aligned}$

式中，r1和r2是介于(0,1)之间的随机数，c1和c2代表学习因子，取值一般为c1=c2=2。

根据速度更新公式可知，粒子的速度由三个部分构成：第一部分是对粒子之前速度的继承，体现了粒子运动的惯性；第二部分是自我认知，表示粒子自身之前的飞行经验对之后飞行方向的影响；第三部分是社会认知，表示种群中所有粒子的飞行经验对每个粒子之后飞行方向的影响。

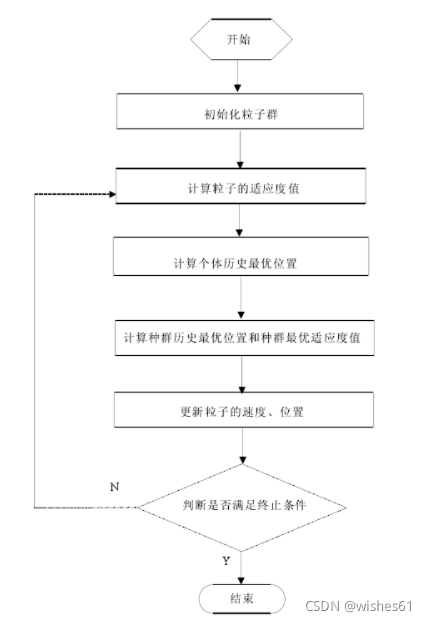
3 实现步骤

Step1：初始化种群：包括搜索空间的上限和下限，两个学习因子c1，c2，算法的最大迭代次数T，每个粒子速度的上限和下限。随机初始化种群中每个粒子的位置和速度.

Step2：根据适应度函数计算每个粒子的适应值fitness，保存每个粒子的最优位置，保存个体最佳适应度值和群体迄今的最好位置.

Step3：根据速度、位置更新公式来更新速度和位置.

Step4：计算更新后每个粒子的适应度值，将每个粒子的最佳适应度值与其历史最优位置时的适应度值比较，如果较好，则将其当前的位置作为该粒子的最优位置.

Step5：对每个粒子，将它的最优位置对应的适应度值与种群最佳适应度值对比，如果更优，则更新种群最优位置和最佳适应度值.

Step6：判断搜索到的结果是否满足停止条件（达到最大迭代次数或满足精度要求），若满足停止条件则输出最优值，否则转到Step3继续运行直到满足条件为止.

在这里插入图片描述

4 MATLAB代码实现PSO算法

优化问题：求解函数最小值。

$F=\sum_{i=1}^{D} x_{i}^{2}$

4.1. main.m

复制以下代码，粘贴到MATLAB，可直接运行出结果

% 主程序 PSO
clear
close all
clc
 
SearchAgents_no = 30 ; %　种群规模
dim = 10 ; % 粒子维度
Max_iter = 1000 ; %　迭代次数
ub = 5 ;
lb = -5 ;
c1 = 1.5 ; %　学习因子1
c2 = 1.5 ; %　学习因子2
w = 0.8 ; %　惯性权重
vmax = 3 ; %　最大飞行速度
pos = lb + rand(SearchAgents_no,dim).*(ub-lb) ; % 初始化粒子群的位置
v = - vmax +2*vmax* rand(SearchAgents_no,dim) ; % 初始化粒子群的速度
% 初始化每个历史最优粒子
pBest = pos ; 
pbestfit = zeros(SearchAgents_no,1);
for i = 1:SearchAgents_no
pbestfit(i) = sum(pos(i,:).^2) ; 
end
%初始化全局历史最优粒子
[gBestfit,index] = min(pbestfit) ;
gBest = pos(index,:) ;
Convergence_curve = zeros(Max_iter,1);
 
for t=1:Max_iter
    for i=1:SearchAgents_no
        % 更新个体的位置和速度
        v(i,:) = w*v(i,:)+c1*rand*(pBest(i,:)-pos(i,:))+c2*rand*(gBest-pos(i,:)) ;
        pos(i,:) = pos(i,:)+v(i,:) ;
        % 边界处理
        v(i,:) = min(v(i,:), vmax);
        v(i,:) = max(v(i,:), -vmax);
        pos(i,:) =min(pos(i,:), ub);
        pos(i,:) =max(pos(i,:), lb);
        % 更新个体最优
        f1 = sum(pos(i,:).^2);
        if f1<pbestfit(i)    
           pBest(i,:) = pos(i,:) ;
           pbestfit(i) = f1;
        end
        % 更新全局最优
       if pbestfit(i) < gBestfit
            gBest = pBest(i,:) ;
            gBestfit = pbestfit(i) ;
       end
    end
    % 每代最优解对应的目标函数值
    Convergence_curve(t) = gBestfit; 
    disp(['Iteration = ' num2str(t)  ', Evaluations = ' num2str(gBestfit)]);
end
 
figure('unit','normalize','Position',[0.3,0.35,0.4,0.35],'color',[1 1 1],'toolbar','none')
subplot(1,2,1);
x = -5:0.1:5;y=x;
L=length(x);
f=zeros(L,L);
for i=1:L
    for j=1:L
       f(i,j) = x(i)^2+y(j)^2;
    end
end
surfc(x,y,f,'LineStyle','none');
xlabel('x_1');
ylabel('x_2');
zlabel('F')
title('Objective space')
 
subplot(1,2,2);
semilogy(Convergence_curve,'Color','r','linewidth',1.5)
title('Convergence_curve')
xlabel('Iteration');
ylabel('Best score obtained so far');
 
axis tight
grid on
box on
legend('PSO')
display(['The best solution obtained by PSO is : ', num2str(gBest)]);
display(['The best optimal value of the objective funciton found by PSO is : ', num2str(gBestfit)]);

4.2. 运行结果

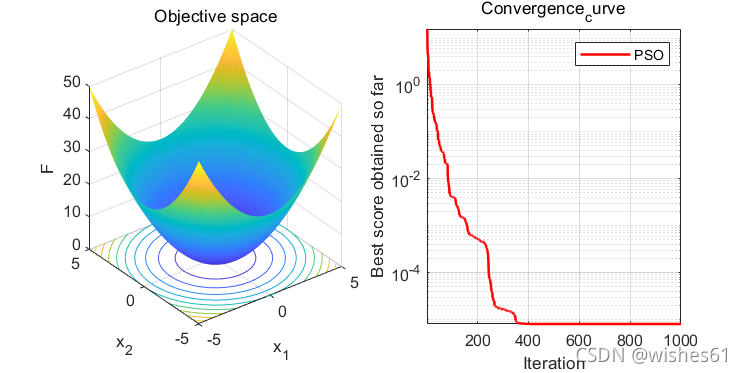
在这里插入图片描述

The best solution obtained by PSO is : -5.9693e-08  4.4549e-07 -1.8445e-08 -1.4353e-07 -2.0883e-07  -2.622e-08   2.743e-08 -1.0503e-08 -7.5957e-08 -6.4972e-07
The best optimal value of the objective funciton found by PSO is : 6.9603e-13
>>