?这一年的题明显的特点是没有很难的算法,全部都是模拟题或者码量题(至少前6题是),很考察代码能力,有点像PTA的感觉,但有很多细节,一不小心就会wa或者t,和国内区域赛不太一样,这就非常考察团队对于机时的把握了。
A - Catch the Plane
题意:
你要从0号点坐公交到1号点,给你m个公交车的起始点、终点、出发时间、到达时间、发车概率,问你选择最优策略时,到达1号点的概率是多少。
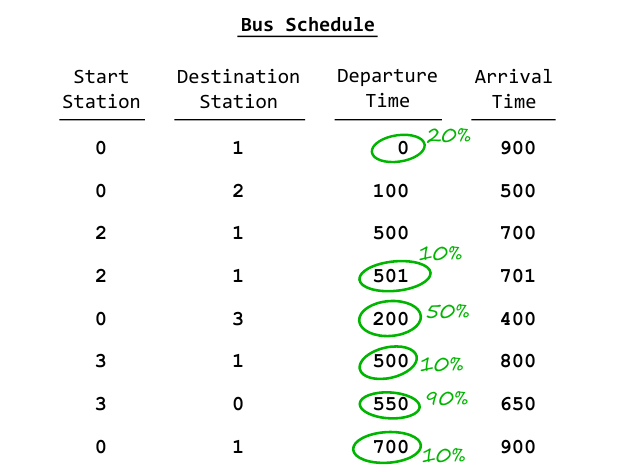
分析:
首先在做策略的时候肯定要考虑坐完公交之后的概率,所以考虑从后往前进行dp。
在dp的时候每个点到达的时间不同,可以到达1号点的概率也不同,很明显有一个单调性,就是越早到达一个点,从这个点到达终点的概率越大,所以我们的dp的状态f_i,代表在某个时间点到达i之后可以到达1号点的最终概率。非常关键的一点就是每个f_i的概率都是关于时间递减的,这样就可以通过二分进行快速的查找dp状态。
代码:
#include<bits/stdc++.h>
using namespace std;
#define K(x...){cerr<<"BEGIN "<<#x<<"->";Err(x);cerr<<" END"<<endl;}
void Err(){}
template<class T, class... A>void Err(T a, A... x){cerr<<a<<','; Err(x...); }
template<class X,class Y,class...A>void Err(pair<X,Y> a,A... x){cerr<<'('<<a.first<<','<<a.second<<')';Err(x...);}
template<template<class...> class T, class t,class...A>void Err(T<t>a,A...x){cerr<<a.size()<<":{ ";for(auto v:a)Err(v),cerr<<",";cerr<<" }";Err(x...); }
typedef long long ll;
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
ll rnd(ll l,ll r){return uniform_int_distribution<ll>(l,r)(rng);}
template<class T>void Min(T &a,const T b){if(a>b)a=b;}
template<class T>void Max(T &a,const T b){if(a<b)a=b;}
#define fi first
#define se second
#define lo (o<<1)
#define ro (o<<1|1)
#define mid ((l+r)/2)
#define endl '\n'
#ifdef ONLINE_JUDGE
#define freopen(a,b,c)
#define K(a...)
#endif
typedef pair<int,int>pii;
typedef vector<int>vi;
const int inf=0x3f3f3f3f;
const ll linf=0x3f3f3f3f3f3f3f3f;
const int N=3e5+10,M=500;
const ll mod=1e9+7;
struct A{
int a,b;
ll c,d;
double e;
};
int main() {
ios::sync_with_stdio(0),cin.tie(0);
freopen("A.in","r",stdin);
int n,m;ll k;cin>>m>>n>>k;
vector<A>ar(m);
for(auto &i:ar)cin>>i.a>>i.b>>i.c>>i.d>>i.e;
sort(ar.begin(),ar.end(),[](A a,A b){return a.c>b.c;});
vector<vector<pair<ll,double>>>f(n);
f[1].push_back({k+1,1});
for(int i=0;i<n;i++)if(i!=1)f[i].push_back({k+1,0});
for(auto i:ar)if(!f[i.b].empty()){
auto it=--lower_bound(f[i.b].begin(),f[i.b].end(),(pair<ll,double>){i.d,2},greater<pair<ll,double>>());
double p=it->se*i.e;
it=--lower_bound(f[i.a].begin(),f[i.a].end(),(pair<ll,double>){i.c,2},greater<pair<ll,double>>());
p+=it->se*(1-i.e);
if(p>f[i.a].back().se)f[i.a].push_back({i.c,p});
}
cout<<fixed<<setprecision(10)<<f[0].back().se;
}B - Comma Sprinkler?
题意
给你若干句子,每个句子里有些单词间有逗号,让你做无限次这种操作,如果一个词前/后面有逗号,所有非开头/结尾的这个词前/后面都加上逗号,最后输出结果句子。
分析
签到题之一,把每个词拆成两个节点,代表这个词前面或后面有逗号,然后如果两个词直接没有句号,就互相连边,最后跑一个搜索就可以了,dfs或者bfs都可以。
代码
#include<bits/stdc++.h>
using namespace std;
#define K(x...){cerr<<"BEGIN "<<#x<<"->";Err(x);cerr<<" END"<<endl;}
void Err(){}
template<class T, class... A>void Err(T a, A... x){cerr<<a<<','; Err(x...); }
template<class X,class Y,class...A>void Err(pair<X,Y> a,A... x){cerr<<'('<<a.first<<','<<a.second<<')';Err(x...);}
template<template<class...> class T, class t,class...A>void Err(T<t>a,A...x){cerr<<"{";for(auto v:a)Err(v);cerr<<"}";Err(x...); }
typedef long long ll;
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
ll rnd(ll l,ll r){return uniform_int_distribution<ll>(l,r)(rng);}
template<class T>void Min(T &a,const T b){if(a>b)a=b;}
template<class T>void Max(T &a,const T b){if(a<b)a=b;}
#define fi first
#define se second
#define lo (o<<1)
#define ro (o<<1|1)
#define mid ((l+r)/2)
#define endl '\n'
#ifdef ONLINE_JUDGE
#define freopen(a,b,c)
#define K(a...)
#endif
typedef pair<int,int>pii;
typedef vector<int>vi;
const int inf=0x3f3f3f3f;
const ll linf=0x3f3f3f3f3f3f3f3f;
const ll mod=1e9+7;
int main() {
ios::sync_with_stdio(0),cin.tie(0);
freopen("A.in","r",stdin);
vector<string>s;
for(string t;cin>>t;)s.push_back(t);
vector<bool> vis(s.size(),0);
set<string>pre,suf;
for(int i=0;i<s.size();i++){
if(s[i].back()=='.'){
vis[i]=1;
s[i].pop_back();
}
else if(s[i].back()==','){
s[i].pop_back();
pre.insert(s[i]);
}
}
map<string,set<string>>to,from;
for(int i=0;i<s.size()-1;i++)if(!vis[i]){
to[s[i]].insert(s[i+1]);
from[s[i+1]].insert(s[i]);
}
queue<pair<int,string>>q;
for(auto i:pre)q.push({0,i});
while(!q.empty()){
int op;string t;tie(op,t)=q.front();q.pop();
if(op==0){
for(auto i:to[t])if(!suf.count(i)){
suf.insert(i);
q.push({1,i});
}
}
else{
for(auto i:from[t])if(!pre.count(i)){
pre.insert(i);
q.push({0,i});
}
}
}
for(int i=0;i<s.size();i++){
cout<<s[i];
if(vis[i])cout<<".";
else if(pre.count(s[i]))cout<<",";
cout<<' ';
}
}
F - Go with the Flow?
题意
定义给你n个单词(长度不超过80),定义河流长度为文本行之间空格形成的间隙(相邻两行间空格列最多差1),让你调整文本宽度,使得河流长度最长。

?分析
签到题之一,直接暴力搜索,枚举一行的长度,从最长单词的长度枚举到长度之和+n-1,其中要做一个剪枝,就是当行数大于已经求出的最大值时需要break掉。
代码
#include<bits/stdc++.h>
using namespace std;
#define K(x...){cerr<<"BEGIN "<<#x<<"->";Err(x);cerr<<" END"<<endl;}
void Err(){}
template<class T, class... A>void Err(T a, A... x){cerr<<a<<','; Err(x...); }
template<class X,class Y,class...A>void Err(pair<X,Y> a,A... x){cerr<<'('<<a.first<<','<<a.second<<')';Err(x...);}
template<template<class...> class T, class t,class...A>void Err(T<t>a,A...x){cerr<<a.size()<<":{ ";for(auto v:a)Err(v),cerr<<",";cerr<<" }";Err(x...); }
typedef long long ll;
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
ll rnd(ll l,ll r){return uniform_int_distribution<ll>(l,r)(rng);}
template<class T>void Min(T &a,const T b){if(a>b)a=b;}
template<class T>void Max(T &a,const T b){if(a<b)a=b;}
#define fi first
#define se second
#define lo (o<<1)
#define ro (o<<1|1)
#define mid ((l+r)/2)
#define endl '\n'
#ifdef ONLINE_JUDGE
#define freopen(a,b,c)
#define K(a...)
#endif
typedef pair<int,int>pii;
typedef vector<int>vi;
const int inf=0x3f3f3f3f;
const ll linf=0x3f3f3f3f3f3f3f3f;
const int N=3e5+10,M=500;
const ll mod=1e9+7;
int main() {
ios::sync_with_stdio(0),cin.tie(0);
freopen("A.in","r",stdin);
int n;cin>>n;
vi ar(n);
int ma=0,sum=n-1;
for(auto &i:ar){
string s;cin>>s;
i=s.size();
Max(ma,i);
sum+=i;
}
int ans=0,id;
for(int len=ma;len<=sum;len++){
vector<vi>f(2,vi(len+1,0));
int st=0,h=1;
for(auto i:ar){
if(st+i>len){
st=0;
h++;
fill(f[h%2].begin(),f[h%2].end(),0);
}
else if(st){
f[h%2][st]=max(f[h%2^1][st],max(f[h%2^1][st-1],f[h%2^1][st+1]))+1;
if(f[h%2][st]>ans){
ans=f[h%2][st];
id=len;
}
}
st+=i+1;
}
if(h<=ans)break;
}
cout<<id<<' '<<ans;
}
H - Single Cut of Failure
题意
在一个宽高w,h的门里,有n条线段,每条线段的两端点都在不同的边上,且不在四个角上。
现在让你画最少的线段(红色的那个),使n个线段每个至少交一次,你画的线段也是端点要在不同的边上(可以是小数),但不能在边上。
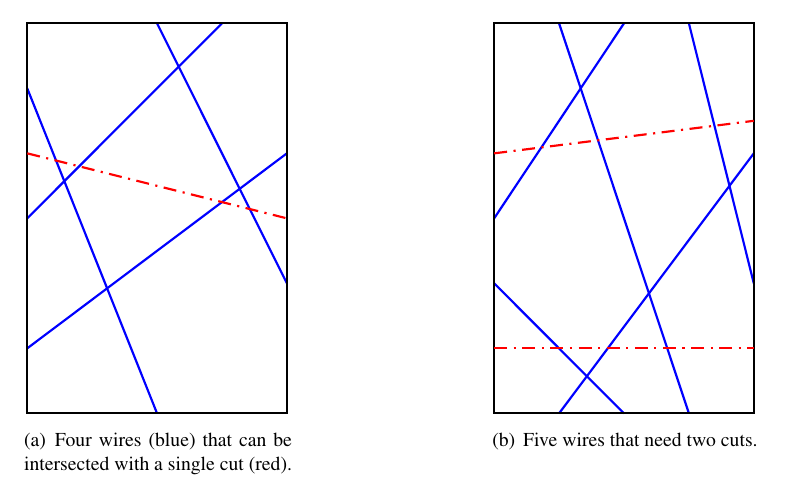
?分析
仔细思考后可以发现一定最多只用画两条,就是两条对角线(稍微歪0.5),就一定可以交出所有线段,所以我们唯一要做的就是看能否一条线段镐定。
我们把每个端点按照顺时针排好序,如果存在一条线段交全部,那么一定是有连续n个标号分别是n个线段里面不同的标号,我们把端点二维坐标转换成一维值,双指针扫一遍就可以判断出来了。
至于方案就直接把点减去0.5就好了。
代码
#include<bits/stdc++.h>
using namespace std;
#define K(x...){cerr<<"BEGIN "<<#x<<"->";Err(x);cerr<<" END"<<endl;}
void Err(){}
template<class T, class... A>void Err(T a, A... x){cerr<<a<<','; Err(x...); }
template<class X,class Y,class...A>void Err(pair<X,Y> a,A... x){cerr<<'('<<a.first<<','<<a.second<<')';Err(x...);}
template<template<class...> class T, class t,class...A>void Err(T<t>a,A...x){cerr<<a.size()<<":{ ";for(auto v:a)Err(v),cerr<<",";cerr<<" }";Err(x...); }
typedef long long ll;
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
ll rnd(ll l,ll r){return uniform_int_distribution<ll>(l,r)(rng);}
template<class T>void Min(T &a,const T b){if(a>b)a=b;}
template<class T>void Max(T &a,const T b){if(a<b)a=b;}
#define fi first
#define se second
#define lo (o<<1)
#define ro (o<<1|1)
#define mid ((l+r)/2)
#define endl '\n'
#ifdef ONLINE_JUDGE
#define freopen(a,b,c)
#define K(a...)
#endif
typedef pair<int,int>pii;
typedef vector<int>vi;
const int inf=0x3f3f3f3f;
const ll linf=0x3f3f3f3f3f3f3f3f;
const int N=3e5+10,M=500;
const ll mod=1e9+7;
int main() {
ios::sync_with_stdio(0),cin.tie(0);
freopen("A.in","r",stdin);
int n;int w,h;
cin>>n>>w>>h;
auto xyto=[&](int x,int y){
if(x==0)return y;
else if(y==h)return h+x;
else if(x==w)return h*2+w-y;
else return h*2+w*2-x;
};
auto toxy=[&](double a){
double x,y;
if(a<h)x=0,y=a;
else if(a<h+w)x=a-h,y=h;
else if(a<h*2+w)x=w,y=h*2+w-a;
else x=h*2+w*2-a,y=0;
return (pair<double,double>){x,y};
};
vi v;
for(int i=0;i<n;i++){
int x,y;cin>>x>>y;
v.push_back(xyto(x,y));
cin>>x>>y;
v.push_back(xyto(x,y));
}
vi rk(n*2);iota(rk.begin(),rk.end(),0);
sort(rk.begin(),rk.end(),[&](int a,int b){
return v[a]<v[b];
});
vi vis(n,0);
int cnt=0,id=-1;
for(int i=0;i<n;i++)if(++vis[rk[i]/2]==1)cnt++;
for(int i=0,j=n;i<n;i++,j++){
if(cnt==n){
id=i;
break;
}
if(--vis[rk[i]/2]==0)cnt--;
if(++vis[rk[j]/2]==1)cnt++;
}
cout<<fixed;
if(~id){
double a=v[rk[id]]-0.5,b=v[rk[id+n]]-0.5;
cout<<1<<endl;
cout<<toxy(a).fi<<' '<<toxy(a).se<<' '<<toxy(b).fi<<' '<<toxy(b).se<<endl;
}
else{
cout<<2<<endl;
cout<<"0 0.5 "<<w<<' '<<h-0.5<<endl;
cout<<"0 "<<h-0.5<<' '<<w<<" 0.5"<<endl;
}
}
I - Triangles
题意
给你一个字符串组成图形,问里面有多少个三角形。
分析
首先要把这个图形模拟出来,因为三角形分为正三角和倒三角(上面的边是平的),所以可以用一个小技巧,写一个函数,然后把三角形图形正着倒着做两遍。
之后一个难点是如何计数,如果暴力来求的话复杂度很高,所以要用到一些数据结构优化,我们考虑以横着的边作为参考,沿着横着的边从左到右进行枚举,然后对于两条斜着的边,一条用树状数组记录合法点,一条用直接查询区间内合法个数。这样做的原因有一个很重要的性质,就是当沿着横着的边走的,如果一条斜边不够长了,那么之后也不会用到这条斜边,也就是合法的边是具有单调性的,这样就很适合使用数据结构来维护。
代码
#include<bits/stdc++.h>
using namespace std;
#define K(x...){cerr<<"BEGIN "<<#x<<"->";Err(x);cerr<<" END"<<endl;}
void Err(){}
template<class T, class... A>void Err(T a, A... x){cerr<<a<<','; Err(x...); }
template<class X,class Y,class...A>void Err(pair<X,Y> a,A... x){cerr<<'('<<a.first<<','<<a.second<<')';Err(x...);}
template<template<class...> class T, class t,class...A>void Err(T<t>a,A...x){cerr<<"{";for(auto v:a)Err(v);cerr<<"}";Err(x...); }
typedef long long ll;
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
ll rnd(ll l,ll r){return uniform_int_distribution<ll>(l,r)(rng);}
template<class T>void Min(T &a,const T b){if(a>b)a=b;}
template<class T>void Max(T &a,const T b){if(a<b)a=b;}
#define fi first
#define se second
#define lo (o<<1)
#define ro (o<<1|1)
#define mid ((l+r)/2)
#define endl '\n'
#ifdef ONLINE_JUDGE
#define freopen(a,b,c)
#define K(a...)
#endif
typedef pair<int,int>pii;
typedef vector<int>vi;
const int inf=0x3f3f3f3f;
const ll linf=0x3f3f3f3f3f3f3f3f;
const ll mod=1e9+7;
struct BIT{
vector<ll>a;
BIT(int n):a(n,0){}
void add(int p,ll x){for(p++;p<=a.size();p+=p&-p)a[p-1]+=x;}
ll sum(int p){ll ret=0;for(p++;p>0;p&=p-1)ret+=a[p-1];return ret;}
};
int main() {
ios::sync_with_stdio(0),cin.tie(0);
freopen("A.in","r",stdin);
int r,c;cin>>r>>c;
vector<string>ar(r*2-1);
getline(cin,ar[0]);
for(auto &i:ar){
getline(cin,i);
i.resize(2*c-1,' ');
}
ll ans=0;
auto solve=[&](){
vector<vi>vl(r,vi(c)),vr(r,vi(c));
for(int i=1;i<r;i++){
BIT sw(c);
set<pii>s;
for(int j=ar[i*2][0]==' ';j<c;j+=2){
int x=i*2,y=j*2;
vl[i][j]=j==0||ar[x-1][y-1]==' '?0:vl[i-1][j-1]+1;
vr[i][j]=j==c-1||ar[x-1][y+1]==' '?0:vr[i-1][j+1]+1;
ans+=sw.sum(j)-sw.sum(j-vl[i][j]*2-1);
s.insert({j+vr[i][j]*2,j});
sw.add(j,1);
while(!s.empty()&&(j+2>=c||ar[x][y+1]==' '||s.begin()->fi==j)){
sw.add(s.begin()->se,-1);
s.erase(s.begin());
}
}
}
};
solve();
reverse(ar.begin(),ar.end());
solve();
cout<<ans;
}
?
K - Wireless is the New Fiber
题意
给你一个n个点的无向连通图,让你构造一个大小为n的树,使得这个树和原先的图相同度数的点尽可能多。
分析
签到题之一,由于原图连通所以度数和肯定是大于等于树的度数和(2n-2)的,所以我们考虑贪心的来构造,肯定是度数越小的点越容易保持度数不变,那么我们把度数排好序,贪心地来取尽可能多的k,使得,这样就算出个数了。
之后剩下的就是方案了,我们保持这k个点的度不变,然后把剩下的n-k个点的度数确定(随便一种就好),使得度数和等于2n-2,那么我们根据度数构造树就可以直接贪心了,从大到小连边。
代码
#include<bits/stdc++.h>
using namespace std;
#define K(x...){cerr<<"BEGIN "<<#x<<"->";Err(x);cerr<<" END"<<endl;}
void Err(){}
template<class T, class... A>void Err(T a, A... x){cerr<<a<<','; Err(x...); }
template<class X,class Y,class...A>void Err(pair<X,Y> a,A... x){cerr<<'('<<a.first<<','<<a.second<<')';Err(x...);}
template<template<class...> class T, class t,class...A>void Err(T<t>a,A...x){cerr<<"{";for(auto v:a)Err(v);cerr<<"}";Err(x...); }
typedef long long ll;
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
ll rnd(ll l,ll r){return uniform_int_distribution<ll>(l,r)(rng);}
template<class T>void Min(T &a,const T b){if(a>b)a=b;}
template<class T>void Max(T &a,const T b){if(a<b)a=b;}
#define fi first
#define se second
#define lo (o<<1)
#define ro (o<<1|1)
#define mid ((l+r)/2)
#define endl '\n'
#ifdef ONLINE_JUDGE
#define freopen(a,b,c)
#define K(a...)
#endif
typedef pair<int,int>pii;
typedef vector<int>vi;
const int inf=0x3f3f3f3f;
const ll linf=0x3f3f3f3f3f3f3f3f;
const int N=3e5+10,M=500;
const ll mod=1e9+7;
int main() {
ios::sync_with_stdio(0),cin.tie(0);
freopen("A.in","r",stdin);
int n,m;cin>>n>>m;
vi du(n);
for(int i=0;i<m;i++){
int a,b;cin>>a>>b;
du[a]++;du[b]++;
}
vi rk(n);iota(rk.begin(),rk.end(),0);
sort(rk.begin(),rk.end(),[&](int a,int b){return du[a]<du[b];});
int k=0,sum=0;
while(k<n){
sum+=du[rk[k]];
if(sum+n-k-1>2*n-2)break;
k++;
}
if(k<n)du[rk[k]]-=sum+n-k-1-2*n+2;
for(int i=k+1;i<n;i++)du[rk[i]]=1;
sort(rk.begin(),rk.end(),[&](int a,int b){return du[a]>du[b];});
cout<<(n-k)<<endl;
cout<<n<<' '<<n-1<<endl;
for(int i=0,j=1;j<n;j++){
cout<<rk[i]<<' '<<rk[j]<<endl;
du[rk[i]]--,du[rk[j]]--;
while(i<n&&du[rk[i]]==0)i++;
}
}