剑指Offer II 022. 链表中环的入口节点

环形链表 II

剑指Offer II 024. 反转链表

剑指 Offer 24. 反转链表

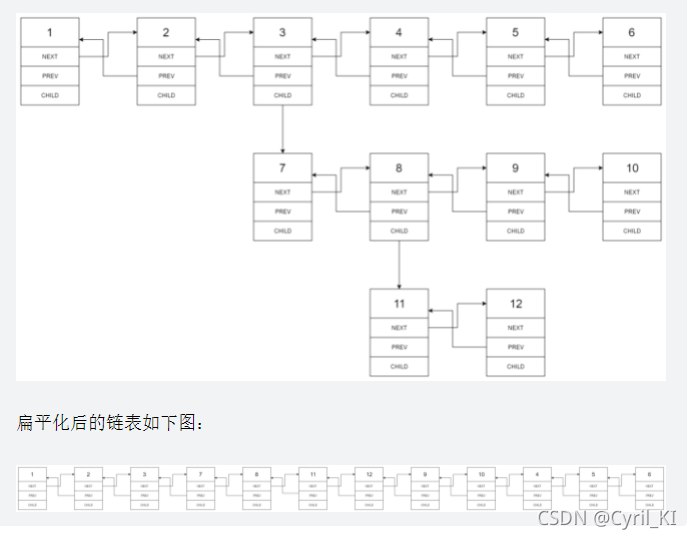
剑指 Offer II 028. 展平多级双向链表

在这里插入图片描述
分析：
??类似于图的深度优先遍历：如果某个结点存在child则就优先遍历child，一直递归到无路可走时逐个返回，再访问其它结点。所以可以先dfs访问所有结点保存，然后逐个链接。
代码：

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* prev;
    Node* next;
    Node* child;
};
*/

class Solution {
private:
    vector<Node*> res;
    unordered_map<Node*, int> mp;
public:
    void dfs(Node* head) {
        res.push_back(head);
        cout << head->val << " ";
        mp[head] = 1;
        if(head->child && mp[head->child] == 0) {
            dfs(head->child);
        }
        if(head->next && mp[head->next] == 0) {
            dfs(head->next);
        }
    }
    Node* flatten(Node* head) {
        if(head == NULL) {
            return head;
        }
        dfs(head);
        //从res中使用尾插法建表
        Node* tail = new Node(0);
        Node* ans = tail;
        for(Node* x : res) {
            tail->next = x;
            x->prev = tail;
            tail = x;
        }
        return ans->next;
    }
};

剑指Offer II 036. 后缀表达式

逆波兰表达式求值

剑指Offer II 037. 小行星碰撞

在这里插入图片描述
分析：
??栈：假设栈顶小行星为top，当前新来了一个小行星new，如果new向左运行，top向右运动，则必然发生爆炸（爆炸后还可能继续爆炸，要一直判断），根据绝对值大小判断即可；否则将new加入栈，栈中的所有行星都能够稳定存在。
代码：

class Solution {
public:
    vector<int> asteroidCollision(vector<int>& asteroids) {
        stack<int> s;
        s.push(INT_MIN);  //预置向左运动的最大质量的行星
        for(auto n : asteroids) {
            if(n < 0) {   //新的小行星向左运动，有可能发生爆炸
                while (s.top() > 0 && s.top() < -n) {  //栈顶大于0，向右运动，且栈顶绝对值更小
                    s.pop();  //栈顶爆炸
                }
                if(s.top() < 0) {
                    s.push(n);  //栈顶小行星也向左运动，二者可以平衡，直接入栈
                }else if(s.top() == -n){  //二者对撞，一起消失
                    s.pop();
                }
            }else {
                s.push(n);  //新的小行星向右运动，肯定不会发生爆炸
            }
        }
        vector<int> res;
        while(!s.empty()) {
            res.push_back(s.top());
            s.pop();
        }
        res.pop_back();
        reverse(res.begin(), res.end());
        return res;
    }
};

剑指Offer II 038. 每日温度

每日温度

剑指Offer II 099. 最小路径之和

最小路径和

剑指Offer II 100. 三角形中最小路径之和

三角形最小路径和

剑指Offer II 101. 分割等和子串

分割等和子集

剑指Offer II 102. 加减的目标值

目标和

剑指Offer II 103. 最少的硬币数目

在这里插入图片描述
分析：
??动态规划：设dp[i]表示凑成总金额为i所需的最少硬币数目，最终返回dp[amount]；初始：dp[0]=0；边界条件：

dp[i] = min(dp[i], dp[i - coins[j]] + 1);

??即：对于dp[i]，它可以由dp[i-coins[j]]再加上一枚coins[j]来凑成，但是j有多种取值，所以我们需要循环判断然后取最小值。此题与完全平方数思路类似。
代码：

class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        int Max = amount + 1;
        vector<int> dp(amount + 1, Max);
        dp[0] = 0;
        for (int i = 1; i <= amount; ++i) {
            for (int j = 0; j < (int)coins.size(); ++j) {
                if (coins[j] <= i) {
                    dp[i] = min(dp[i], dp[i - coins[j]] + 1);
                }
            }
        }
        return dp[amount] > amount ? -1 : dp[amount];
    }
};