背包问题：

01背包问题

地址：

https://www.acwing.com/problem/content/2/

描述：

思路：

二维数组：

简化为一维数组：

为什么可以简化的原因

?必须要的原因：

代码：

二位数组：

第一种写法便于我们理解（可用于理解，直接看下面优化版）

#include <iostream>
using namespace std;
//N是物品个数，V是容量
int N,V;
const int M=1e3;
//存放某个物品所占的体积和容量
int v[M],w[M];
//f[i][j]前 i 个物品，背包容量 j 下的最优解（最大价值）
int f[M][M];
int main(){
    cin>>N>>V;
    for(int i=1;i<=N;i++) cin>>v[i]>>w[i];
    //显然当i=0，即我们一样物品都不拿时=>f[0][0~m]=0，所以i从1开始
    for(int i=1;i<=N;i++){
        for(int j=0;j<=V;j++){
            //假如说当前背包装不下我们的第i件物品，因此前 i个物品最优解即为前 i?1个物品最优解
            if(j<v[i]){
                f[i][j]=f[i-1][j];
            }
            else{
                f[i][j]=max(f[i-1][j],f[i-1][j-v[i]]+w[i]);
            }
        }
    }//for(i)
    cout<<f[N][V]<<endl;
    return 0;
}

?当然这里我们可以再进行一次优化

#include <iostream>
using namespace std;
//N是物品个数，V是容量
int N,V;
const int M=1e3;
//存放某个物品所占的体积和容量
int v[M],w[M];
//f[i][j]前 i 个物品，背包容量 j 下的最优解（最大价值）
int f[M][M];
int main(){
    cin>>N>>V;
    for(int i=1;i<=N;i++) cin>>v[i]>>w[i];
    //显然当i=0，即我们一样物品都不拿时=>f[0][0~m]=0，所以i从1开始
    for(int i=1;i<=N;i++){
        for(int j=0;j<=V;j++){
            //不管三七二十一我们先假设当前背包装不下我们的第i件物品，
            //因此前 i个物品最优解即为前 i?1个物品最优解
                f[i][j]=f[i-1][j];
            //假设实际能装下第i件物品，我们将不能装下和能装下两者进行比较取最大值
                f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);
        }
    }//for(i)
    cout<<f[N][V]<<endl;
    return 0;
}

?一维数组：

#include <iostream>
using namespace std;
//N是物品个数，V是容量
int N,V;
const int M=1e3+10;
//存放某个物品所占的体积和容量
int v[M],w[M];
int f[M];
int main(){
    cin>>N>>V;
    for(int i=1;i<=N;i++) cin>>v[i]>>w[i];
    for(int i=1;i<=N;i++){
        for(int j=V;j>=v[i];j--){
           f[j]=max(f[j],f[j-v[i]]+w[i]);
        }
    }
    cout<<f[V]<<endl;
    return 0;
}

完全背包问题

地址：

https://www.acwing.com/problem/content/3/

描述：

思想：

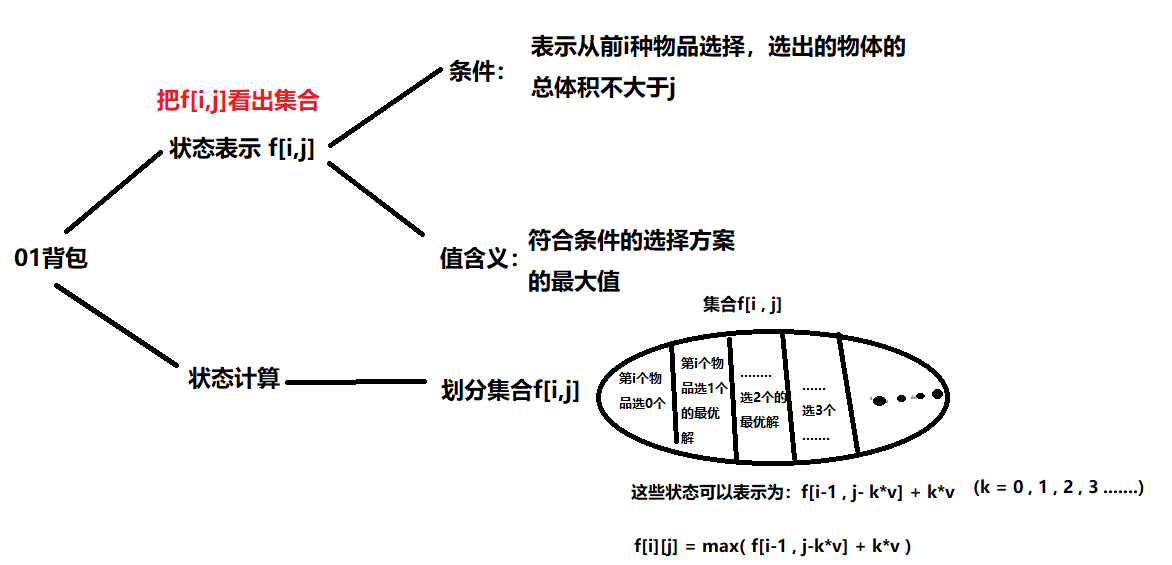
?优化思路：

代码：?

优化前：

#include <iostream>
using namespace std;
int N,V;
const int M=1e3+10;
int f[M][M];
int v[M],w[M];
int main(){
    cin>>N>>V;
    for(int i=1;i<=N;i++)cin>>v[i]>>w[i];
    for(int i=1;i<=N;i++){
        for(int j=0;j<=V;j++){
            for(int k=0;k*v[i]<=j;k++){
                f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+w[i]*k);
            }
        }
    }//for(i)
    cout<<f[N][V];
}

?优化后：

#include <iostream>
using namespace std;
int N,V;
const int M=1e3+10;
int f[M][M];
int v[M],w[M];
int main(){
    cin>>N>>V;
    for(int i=1;i<=N;i++)cin>>v[i]>>w[i];
    for(int i=1;i<=N;i++){
        for(int j=1;j<=V;j++){
            f[i][j]=f[i-1][j];
            if(v[i]<=j) f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);
        }
    }//for(i)
    cout<<f[N][V];
}

?再次优化成一维数组

这里不需要进行逆序操作

#include <iostream>
using namespace std;
int N,V;
const int M=1e3+10;
int f[M];
int v[M],w[M];
int main(){
    cin>>N>>V;
    for(int i=1;i<=N;i++)cin>>v[i]>>w[i];
    for(int i=1;i<=N;i++){
        for(int j=v[i];j<=V;j++){
        f[j]=max(f[j],f[j-v[i]]+w[i]);
        }
    }//for(i)
    cout<<f[V];
}