题意:
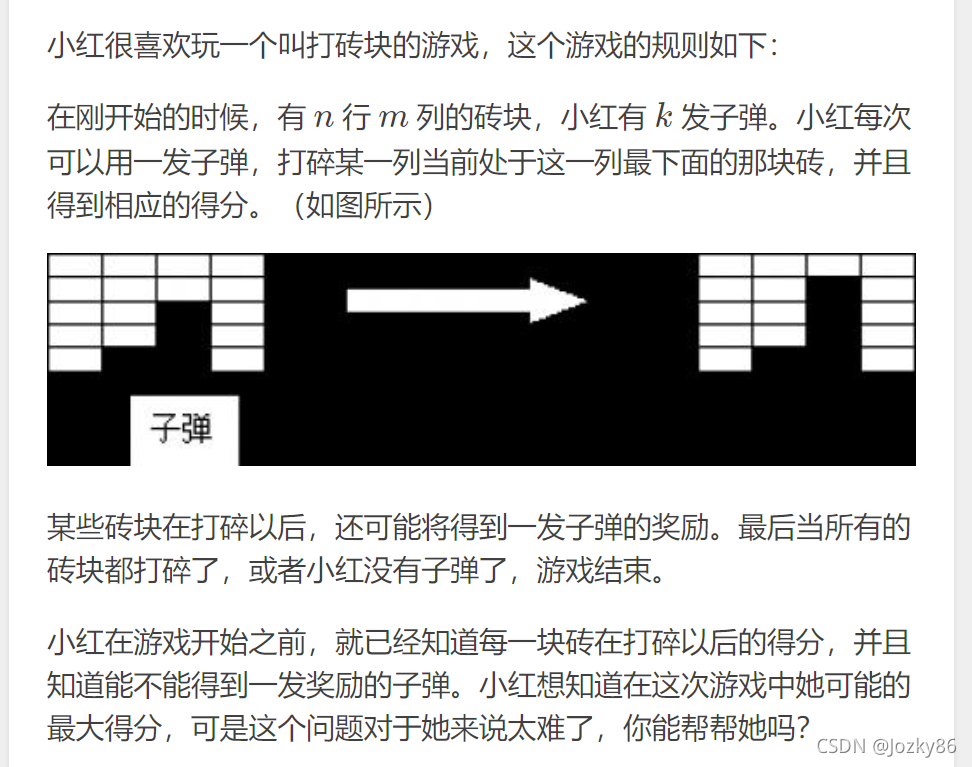
题解:
参考题解:
I_AM_HelloWord
danxmz2006
这两个博客结合看,大致就能理解
我们只在N处转移,面对Y类的块无需决策,因为Y类的块可以一直打
不同的打砖块的顺序,决定了我们最后的分数情况,因此有个结论:
我们最后一个打的砖块一定是N类砖块,除非所有的砖块都已经打完了
我们从这点出发开始转移:
对于计算[1,j]列的最优解时:
- 第j列根本不打(此时直接继承[1,j-1]的状态)
- 最后一发子弹在第j列上
- 最后一发子弹在[1,j-1]列
- 最后一发子弹还未出现(即最后一发子弹将会在[j+1,m]中,不过我们无需管)
状态转移中我们需要一些辅助变量:
sum1[i][j]表示对于第i列,打到第j行所得分数
sum2[i][j]表示对于第i列,打到第j行同时与此块相邻的一连串Y全部打掉能得到的分数(可以理解成在第i列,第j行开始打块,所能打的最大分)
tot[i][j]:表示对于第i列打到第j行所需要的子弹数量(对于N类砖块,数量+1,对于Y类不变)
设dp[j][tk][0/1]:表示[1,j]列中,用tk发子弹,最后一发子弹是否在[1,j]列中,0表示在,1表示不在
这样转移我们充分考虑了以每一列是否为结尾的情况
转移1:
//直接继承上一列的状态
dp[j][tk][0]= dp[j - 1][tk][0];
dp[j][tk][1]= dp[j - 1][tk][1];
转移2:
最后一发子弹在[1,j]中,同时在第j列,因此不在[1,j-1]中
dp[j][k][0]=max(dp[j-1][k-tot[j][i]][1]+sum1[j][i])
转移3:
最后一发子弹在[1,j]中,但不在第j列,因此在[1,j-1]中
dp[j][k][0]=max(dp[j-1][k-tot[j][i]][0]+sum2[j][i])
转移4:
最后一发子弹不在[1,j]中,因此[1,j-1]必然没有,第j列也没有
dp[j][k][1]=max(dp[j-1][k-tot[j][i]][1]+sum2[j][i])
代码:
#include <bits/stdc++.h>
#include <unordered_map>
#define debug(a, b) printf("%s = %d\n", a, b);
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> PII;
clock_t startTime, endTime;
//Fe~Jozky
const ll INF_ll= 1e18;
const int INF_int= 0x3f3f3f3f;
void read(){};
template <typename _Tp, typename... _Tps> void read(_Tp& x, _Tps&... Ar)
{
x= 0;
char c= getchar();
bool flag= 0;
while (c < '0' || c > '9')
flag|= (c == '-'), c= getchar();
while (c >= '0' && c <= '9')
x= (x << 3) + (x << 1) + (c ^ 48), c= getchar();
if (flag)
x= -x;
read(Ar...);
}
template <typename T> inline void write(T x)
{
if (x < 0) {
x= ~(x - 1);
putchar('-');
}
if (x > 9)
write(x / 10);
putchar(x % 10 + '0');
}
void rd_test()
{
#ifdef LOCAL
startTime= clock();
freopen("in.txt", "r", stdin);
#endif
}
void Time_test()
{
#ifdef LOCAL
endTime= clock();
printf("\nRun Time:%lfs\n", (double)(endTime - startTime) / CLOCKS_PER_SEC);
#endif
}
const int maxn= 210;
int cur[maxn], tot[maxn][maxn], a[maxn][maxn];
int b[maxn][maxn];
int sum1[maxn][maxn];
int sum2[maxn][maxn];
int dp[maxn][maxn][2];
int main()
{
//rd_test();
int n, m, k;
read(n, m, k);
//n行m列k个子弹
// memset(a, 0, sizeof(a));
// memset(b, 0, sizeof(b));
// memset(sum2, 0, sizeof(sum2));
// memset(sum1, 0, sizeof(sum1));
// memset(cur, 0, sizeof(cur));
// memset(tot, 0, sizeof(tot));
//memset(cur,0x3f3f3f,sizeof(cur));
for (int i= n; i >= 1; i--) {
for (int j= 1; j <= m; j++) {
read(a[i][j]);
char ch= getchar();
while (ch < 'A' || ch > 'Z')
ch= getchar();
if (ch == 'Y')
b[i][j]= 1; //对于Y砖标记
}
}
int ans= 0;
for (int j= 1; j <= m; j++) {
for (int i= 1; i <= n; i++) {
if (b[i][j] == 0) //如果是N
{
cur[j]= i; //记录了每一列第一次出现N的位置
break;
}
ans+= a[i][j]; //记录Y的分数
}
}
//先求sum1
for (int j= 1; j <= m; j++) {
for (int i= cur[j]; i <= n; i++) {
sum1[j][i]= sum1[j][i - 1] + a[i][j];
sum2[j][i]= sum1[j][i];
}
}
//利用求sum2
for (int j= 1; j <= m; j++) {
tot[j][cur[j]]= 1; //第j列打到第cur[j]行所需的子弹数量
for (int i= cur[j]; i <= n; i++) {
int idx= i;
while (b[idx + 1][j]) //如果第idx+1行的第j列
idx++;
//找到这一列连续Y的位置,用于更新sum2
sum2[j][i]= sum1[j][idx];
//sum2比起sum1多的是连续Y的数量,所以直接更新sum1[j][idx]
tot[j][idx + 1]= tot[j][i] + 1;
//只需要多一个子弹即可,因为打Y不耗费额外的
i= idx;
}
}
//以上为更新sum1和sum2的步骤
for (int j= 0; j <= m; j++)
dp[j][0][0]= -INF_int;
for (int j= 1; j <= m; j++) { //[1,j]列中
for (int tk= 1; tk <= k; tk++) { //用了k发子弹
dp[j][tk][0]= dp[j - 1][tk][0]; //直接继承上一列的状态
dp[j][tk][1]= dp[j - 1][tk][1];
if(cur[j]==0)continue;//说明这一列都是Y,直接跳过就行
for (int i= cur[j]; i <= n; i++) //枚举每一行
if (!b[i][j] && tk >= tot[j][i]) {
//如果第i行,第j列是N,并且子弹数量大于需要的数量
//就进行状态转移
dp[j][tk][0]= max(dp[j][tk][0], dp[j - 1][tk - tot[j][i]][1] + sum1[j][i]);
dp[j][tk][0]= max(dp[j][tk][0], dp[j - 1][tk - tot[j][i]][0] + sum2[j][i]);
dp[j][tk][1]= max(dp[j][tk][1], dp[j - 1][tk - tot[j][i]][1] + sum2[j][i]);
}
}
}
printf("%d\n", dp[m][k][0] + ans);
return 0;
//Time_test();
}
/*
1 5 185
3985 Y 6951 N 2151 Y 1749 N 7413 Y
*/
