一、快速排序
通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
算法实现
在数组中选择一个数,分别从数组的两端扫描数组,
从后半部分开始,如果发现有元素比该基准点的值小,就交换位置
然后从前半部分开始扫描,发现有元素大于基准点的值,继续交换位置
如此往复循环,让这个点左边都比他小,右边都比他大
之后继续采用递归的方式分别对前半部分和后半部分排序,当前半部分和后半部分均有序时该数组就自然有序了。
复杂度

?
代码示例
void QSort(SqList *L, int low, int high)
{
int pivot;
if(low < high)
{
pivot = Partition(L, low, high);
QSort(L, low,, pivot - 1);
QSort(L, pivot + 1, high);
}
}
int Partition(SqList *L, int low, int high)
{
int pivotkey;
pivotkey = L->r[low];
while(low < high)
{
while(low < high && L->r[high] >= pivotkey)
high--;
swap(L, low, high);
while(low < high && L->r[low] <= pivotkey)
low++;
swap(L, low, high);
}
return low;
}图示过程
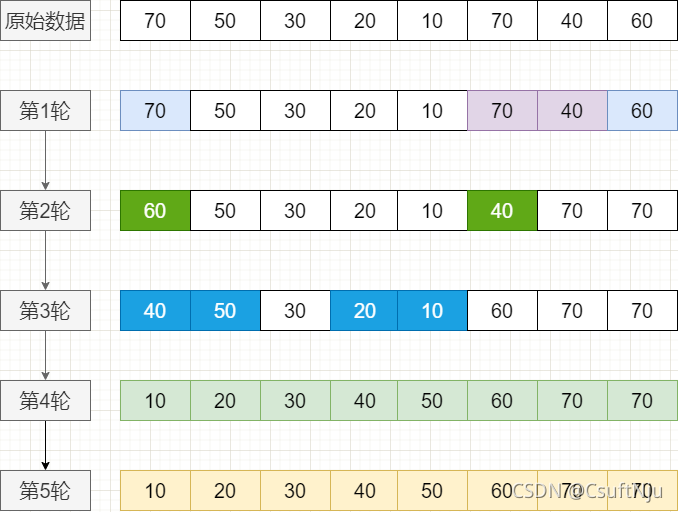
?二、计数排序
计数排序是将输入的数据值转化为键存储在额外开辟的数组空间中。计数排序算法不是基于元素比较,而是利用数组下标来确定元素的正确位置。
算法实现
1. 找出待排序的数组中最大和最小的元素
2.统计数组中每个值为i的元素出现的次数,存入数组C的第i项
3.对所有的计数累加(从C中的第一个元素开始,每一项和前一项相加)
4.反向填充目标数组:将每个元素i放在新数组的第C(i)项,每放一个元素就将C(i)减去1
复杂度
?
?代码示例
void CountSort(int *arr, int len){
if(arr == NULL) return;
int max = arr[0], min = arr[0];
for(int i = 1; i < len; i++){
if(arr[i] > max) max = arr[i];
if(arr[i] < min) min = arr[i];
}
int size = max - min + 1;
int *count =(int*)malloc(sizeof(int)*size);
memset(count, 0, sizeof(int)*size);
for(int i = 0; i < len; i++)
count[arr[i] - min]++;//包含了自己!
for(int i = 1; i < size; i++)
count[i] += count[i - 1];
int* psort =(int*)malloc(sizeof(int)*len);
memset(psort, 0, sizeof(int)*len);
for(int i = len - 1; i >= 0; i--){
psort[count[arr[i] - min]] = arr[i];
count[arr[i] - min]--;
}
for(int i = 0; i < len; i++){
arr[i] = psort[i];
}
free(count);
free(psort);
count = NULL;
psort = NULL;
}?三、桶排序
桶排序的原理是划分多个范围相同的区间,每个子区间自排序,最后合并,是计数排序的扩展版本。计数排序可以看成每个桶只存储相同元素,而桶排序每个桶存储一定范围的元素,通过映射函数,将待排序数组中的元素映射到各个对应的桶中,对每个桶中的元素进行排序,最后将非空桶中的元素逐个放入原序列中。
算法实现
根据待排序集合中最大元素和最小元素的差值范围和映射规则,确定申请的桶个数;
遍历待排序集合,将每一个元素移动到对应的桶中;
对每一个桶中元素进行排序,并移动到已排序集合中。
复杂度
空间复杂度为O(N+M),时间复杂度为O(nlog(n / m)),当桶的数量m接近数据个数n时,时间复杂度接近O(n)
代码示例
/* a -- 待排序数组
* n -- 数组a的长度
* max -- 数组a中最大值的范围*/
void bucketSort(int a[], int n, int max)
{
int i,j;
int buckets[max];
// 将buckets中的所有数据都初始化为0。
memset(buckets, 0, max*sizeof(int));
// 1. 计数
for(i = 0; i < n; i++)
buckets[a[i]]++;
// 2. 排序
for (i = 0, j = 0; i < max; i++)
{
while( (buckets[i]--) >0 )
a[j++] = i;
}
}进阶版
#include<iterator>
#include<iostream>
#include<vector>
using namespace std;
const int BUCKET_NUM = 10;
struct ListNode{
explicit ListNode(int i=0):mData(i),mNext(NULL){}
ListNode* mNext;
int mData;
};
ListNode* insert(ListNode* head,int val){
ListNode dummyNode;
ListNode *newNode = new ListNode(val);
ListNode *pre,*curr;
dummyNode.mNext = head;
pre = &dummyNode;
curr = head;
while(NULL!=curr && curr->mData<=val){
pre = curr;
curr = curr->mNext;
}
newNode->mNext = curr;
pre->mNext = newNode;
return dummyNode.mNext;
}
ListNode* Merge(ListNode *head1,ListNode *head2){
ListNode dummyNode;
ListNode *dummy = &dummyNode;
while(NULL!=head1 && NULL!=head2){
if(head1->mData <= head2->mData){
dummy->mNext = head1;
head1 = head1->mNext;
}else{
dummy->mNext = head2;
head2 = head2->mNext;
}
dummy = dummy->mNext;
}
if(NULL!=head1) dummy->mNext = head1;
if(NULL!=head2) dummy->mNext = head2;//这两行好像要改成while?
return dummyNode.mNext;
}
void BucketSort(int n,int arr[]){
vector<ListNode*> buckets(BUCKET_NUM,(ListNode*)(0));
for(int i=0;i<n;++i){
int index = arr[i]/BUCKET_NUM;
ListNode *head = buckets.at(index);
buckets.at(index) = insert(head,arr[i]);
}
ListNode *head = buckets.at(0);
for(int i=1;i<BUCKET_NUM;++i){
head = Merge(head,buckets.at(i));
}
for(int i=0;i<n;++i){
arr[i] = head->mData;
head = head->mNext;
}
}图示过程
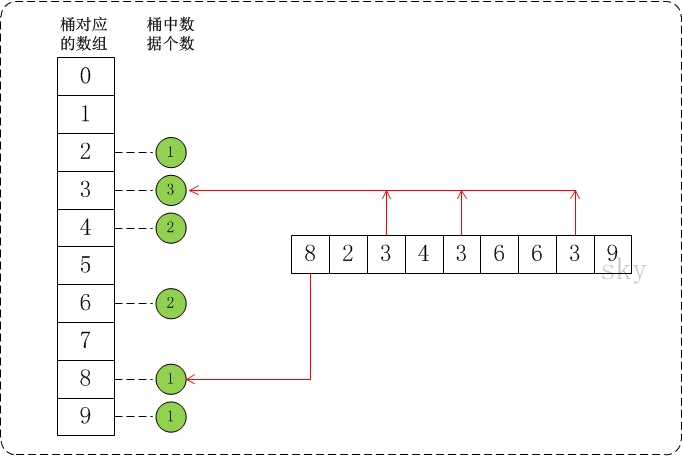
四、基数排序
原理是原理是将整数按位数切割成不同的数字,然后按每个位数分别比较。
算法实现
任何一个阿拉伯数的个位数上的基数都是以0~9来表示的。所以可以把0~9视为10个桶。
根据序列的各个位数的数字来进行分类,将其分到指定的桶中。
分类后从各个桶中,将这些数按照从编号0到编号9的顺序依次将所有数取出来。
得到的序列就是个位数上呈递增趋势的序列。
接下来对十位数、百位数也按照这种方法进行排序,最后就能得到排序完成的序列。
复杂度

?代码示例
#include <stdio.h>
#include <string.h>
/* 获取输入数字的索引值,dec指定数字的位数,3代表百位数,order指定需要获取哪一位的索引,1代表个位,2代表十位,3代表百位 */
int get_index(int num, int dec, int order)
{
int i, j, n;
int index;
int div;
/* 根据位数,循环减去不需要的高位数字 */
for (i=dec; i>order; i--) {
n = 1;
for (j=0; j<dec-1; j++)
n *= 10;
div = num/n;
num -= div * n;
dec--;
}
/* 获得对应位数的整数 */
n = 1;
for (i=0; i<order-1; i++)
n *= 10;
/* 获取index */
index = num / n;
return index;
}
/* 进行基数排序 */
void radix_sort(int array[], int len, int dec, int order)
{
int i, j;
int index; /* 排序索引 */
int tmp[len]; /* 临时数组,用来保存待排序的中间结果 */
int num[10]; /* 保存索引值的数组 */
memset(num, 0, 10*sizeof(int)); /* 数组初始清零 */
memset(tmp, 0, len*sizeof(int)); /* 数组初始清零 */
if (dec < order) /* 最高位排序完成后返回 */
return;
for (i=0; i<len; i++) {
index = get_index(array[i], dec, order); /* 获取索引值 */
num[index]++; /* 对应位加一 */
}
for (i=1; i<10; i++)
num[i] += num[i-1]; /* 调整索引数组 */
for (i=len-1; i>=0; i--) {
index = get_index(array[i], dec, order); /* 从数组尾开始依次获得各个数字的索引 */
j = --num[index]; /* 根据索引计算该数字在按位排序之后在数组中的位置 */
tmp[j] = array[i]; /* 数字放入临时数组 */
}
for (i=0; i<len; i++)
array[i] = tmp[i]; /* 从临时数组复制到原数组 */
printf("the %d time\n", order);
for (i=0; i<30; i++)
printf("%d ", array[i]);
printf("\n");
radix_sort(array, len, dec, order+1);/* 继续按高一位的数字大小进行排序 */
return;
}
int main(int argc, char *argv[])
{
int i;
int array[30] = {258, 976, 515, 337, 359, 701, 916, 494, 303, 175,
677, 825, 131, 560, 147, 254, 759, 814, 917, 382,
452, 114, 873, 585, 881, 127, 819, 658, 461, 435};
int len = 30; /* 测试数据个数 */
int dec = 3; /* 数据位数,3代表3位数 */
int order = 1; /* 排序的位数,1代表个位、2代表十位、3代表百位 */
printf("before\n");
for (i=0; i<30; i++)
printf("%d ", array[i]);
printf("\n");
/* 排序函数,从个位开始 */
radix_sort(array, len, dec, order);
printf("final\n");
for (i=0; i<30; i++)
printf("%d ", array[i]);
printf("\n");
return 0;
}