[数据结构与算法]JZ66 机器人的运动范围

描述
地上有一个rows行和cols列的方格。坐标从 [0,0] 到 [rows-1,cols-1]。一个机器人从坐标0,0的格子开始移动，每一次只能向左，右，上，下四个方向移动一格，但是不能进入行坐标和列坐标的数位之和大于threshold的格子。 例如，当threshold为18时，机器人能够进入方格[35,37]，因为3+5+3+7 = 18。但是，它不能进入方格[35,38]，因为3+5+3+8 = 19。请问该机器人能够达到多少个格子？

范围:
1 <= rows, cols<= 100
0 <= threshold <= 20

示例1
输入：
1,2,3
返回值：
3

深度优先遍历
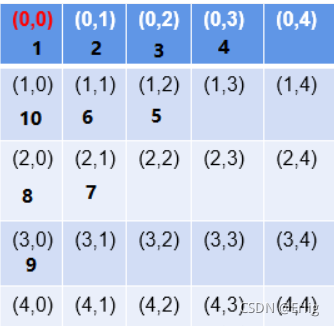
从左上角第一个格子(0,0)进入，则只能有两个方向选择，向右走(i,j+1)和向下走(i+1,j)，然后要判断当前格子坐标元素相加的值是否不大于threshold的值
例如：5，5，3

class Solution:
    def dfs(self,i,j,row,col,threshold,matrix):
        #计算坐标i，j数位相加之和
        tmp1 = i
        tmp2 = j
        flag = 0
        while tmp1:
            flag += tmp1 % 10
            tmp1 = tmp1 // 10
        while tmp2:
            flag += tmp2 % 10
            tmp2 = tmp2 // 10
        #不能继续遍历或已经遍历过的点，则返回0
        if i<0 or i>=row or j<0 or j>=col or matrix[i][j] or flag > threshold :
            return 0
        #否则，能遍历该点，且标记该点被遍历到
        matrix[i][j] = 1
        #遍历该点的下方和右方
        return 1+self.dfs(i+1,j,row,col,threshold,matrix)+self.dfs(i,j+1,row,col,threshold,matrix)
        
    def movingCount(self, threshold, rows, cols):
        #设置一个标记列表，其中1表示该点已经遍历到，0表示还未遍历到
        matrix = [[0 for _ in range(cols)] for _ in range(rows)]
        return self.dfs(0,0,rows,cols,threshold,matrix)