数学专题
- 本次训练包含题目
- Problem A Mysterious Bacteria
- Problem B Harmonic Number
- Problem C Trailing Zeroes (III)
- Problem D Division by 3
- Problem E Dice (I)
- Problem F Goldbach's Conjecture
- Problem G Leading and Trailing
- Problem H Aladdin and the Flying Carpet
- Problem I Sigma Function
- Problem J Bi-shoe and Phi-shoe
- Problem K Lcm与Gcd构造
- Problem L 数列求和
- Problem M 青蛙的约会
- Problem N Primes
- Problem Maximum GCD
- 本次测试包含题目
本次训练包含题目
难度 ★ :1.Harmonic Number 2.Division by 3 3.Goldbach’s Conjecture 4.Lcm与Gcd构造 5.Primes 6.Maximum GCD
难度 ★★ :1.Mysterious Bacteria 2.Trailing Zeroes (III) 3.Dice (I) 4.Leading and Trailing 5.Aladdin and the Flying Carpet 6.数列求和
难度 ★★★ :1.Sigma Function 2.Bi-shoe and Phi-shoe 3.青蛙的约会
Problem A Mysterious Bacteria
题目链接:Mysterious Bacteria
题目分类:质因数分解,最大公约数
题目大意:给定一个32位有符号正数x,求最大的p满足x=b的p次方,b为整数
题目思路:整体思路是将x质因数分解,求个各质因子的幂的最大公约数,这题有两个坑,第一个坑是x可以取负数,这个时候,p就只能取奇数,我们将p中的质偶因子全除掉即可,还有一个坑点是,计算机内,负数的绝对值比正数的最大值的绝对值小一,换句话说就是int存不下题目要求的最小负数,要开long long
AC代码:
#include <bits/stdc++.h>
using namespace std;
vector<int> prime;//素数打表
bitset<50000> isprime;//是不是质数
int gcd(int x, int y) {
return y ? gcd(y, x % y) : x;
}
void pre_process() {
isprime.set();
isprime[0] = isprime[1] = false;
for (int i = 2; i < 50000; i ++) {
if (isprime[i] == true) {
prime.push_back(i);
for (int j = 2 * i; j < 50000; j += i) {
isprime[j] = false;
}
}
}
}
int main() {
int t;
long long x;//卡long long 因为最大正数不能转化为负数
pre_process();//区间筛法,先将可能用到的素数打表
while (~scanf("%d", &t)) {
for (int i = 1; i <= t; i ++) {
bool flag = false;
scanf("%lld", &x);
if (x < 0) {
flag = true;
x = -x;
}
//质因数分解
int ans = 0;
for (unsigned j = 0; j < prime.size() && prime[j] * prime[j] <= x; j ++) {
int c = 0;
while (x % prime[j] == 0) {
c ++;
x /= prime[j];
}
ans = gcd(ans, c);
}
if (x != 1) {//x是质数
ans = 1;
}
if (flag) {
while (ans % 2 == 0) {
ans >>= 1;
}
}
printf("Case %d: %d\n", i, ans);
}
}
return 0;
}

这里补充一下,gcd函数处理负数的特点,我们考虑三种情况
①x为负数,y为正数
②x为正数,y为负数
③x为负数,y为负数
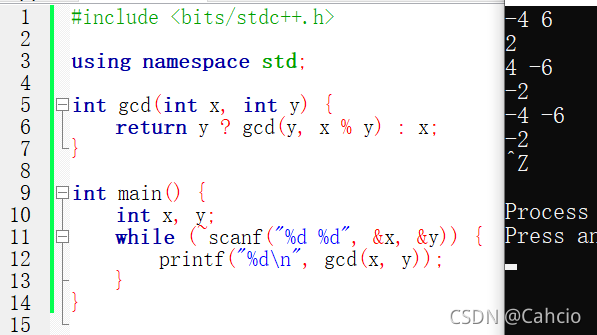
可以看到gcd的正负与y保持一致
Problem B Harmonic Number
题目链接:Harmonic Number
题目分类:签到
题目大意:给定n,求n的调和级数
题目思路:最开始以为这题会卡double精度,其实不会。我们如果直接对1到1e8的数据打表,肯定会MLE,我们就可以采用类似分桶法的思想,每100个数据打一个表即可。这题也可以用欧拉常数做
f(n)≈ln(n)+C+1/2*n,C≈0.57721566490153286060651209,当n很小时,公式不准,我们也可打表做
AC代码:
分块打表
#include <bits/stdc++.h>
using namespace std;
double ans[1000001];
int main() {
int n, t;
double s = 0;
for (int i = 1; i <= 100000000; i ++) {
s += 1.0 / i;
if (i % 100 == 0) {
ans[i / 100] = s;
}
}
while (~scanf("%d", &t)) {
for (int j = 1; j <= t; j ++) {
scanf("%d", &n);
double sum = ans[n / 100];
int k = n % 100;
n -= n % 100;
for (int i = 1; i <= k; i ++) {
sum += 1.0 / (i + n);
}
printf("Case %d: %.10lf\n", j, sum);
}
}
return 0;
}

欧拉常数
#include <bits/stdc++.h>
using namespace std;
const double c = 0.57721566490153286060651209;
double ans[10000];
void pre_process() {
for (int i = 1; i < 10000; i ++) {
ans[i] = ans[i - 1] + 1.0 / i;
}
}
int main() {
pre_process();
int t, n;
scanf("%d", &t);
for (int cc = 1; cc <= t; cc ++) {
scanf("%d", &n);
if (n < 10000) {
printf("Case %d: %.10f\n", cc, ans[n]);
} else {
printf("Case %d: %.10f\n", cc, log(n) + c + 1.0 / (2 * n));
}
}
return 0;
}

Problem C Trailing Zeroes (III)
题目链接:Trailing Zeroes (III)
题目分类:找规律
题目大意:给定q,求一个最小的n,使得n的阶乘尾部恰好有q个0
题目思路:尾部恰好有q个0,那么n的阶乘恰好有q个10,由于2的数量远大于5,就相当于n的阶乘恰好有q个5,简单找找规律可以知道,每5个数就有一个5,每25个数就有两个5……,一个数5的个数为n/5+n/25+n/125…
写成代码就是
while (x) {
x /= 5;
ans += x;
}
再加上二分查找就能得到答案
还有一种思路是借鉴进制的思路,最小单位是1,每5个和成一个大块,第i位ai大小位5i+1,对于q来说,若存在n,一定能表示q=a0×1+a1×6+…+an×(5n+1),根据我们这题的性质每一个ai必须小于等于4(不然就合成了一个大块),再通过对每个块对应个数打表(比如说a1对应25个数)和求进制转化的思路即可解决这道题
AC代码:
二分思路
#include <bits/stdc++.h>
using namespace std;
const int INF = 5e8;
int get(int x) {
int ans = 0;
while (x) {
x /= 5;
ans += x;
}
return ans;
}
int main() {
//freopen("out.txt", "w", stdout);
int t, q;
scanf("%d", &t);
for (int cc = 1; cc <= t; cc ++) {
scanf("%d", &q);
int l = 0, r = INF;
while (r - l > 1) {
int mid = (r + l) >> 1;
if (get(mid) >= q) {
r = mid;
} else {
l = mid;
}
}
int num = get(r);
if (num == q) {
printf("Case %d: %d\n", cc, r);
} else {
printf("Case %d: impossible\n", cc);
}
}
}

进制思路:
#include <bits/stdc++.h>
using namespace std;
int ans[15], l, pow5[15];
int main() {
int n, t;
pow5[0] = 5;
ans[0] = 1;
for (int i = 1; ans[i - 1] * 5 + 1 <= 100000000; i ++) {
pow5[i] = pow5[i - 1] * 5;
ans[i] = ans[i - 1] * 5 + 1;
l = i;
}
while (~scanf("%d", &t)) {
for (int i = 1; i <= t; i ++) {
scanf("%d", &n);
int cnt = 0;
for (int j = l; j >= 0; j --) {
if (n / ans[j] > 4) {
break;
}
cnt += (n / ans[j]) * pow5[j];
n %= ans[j];
}
if (n != 0) {
printf("Case %d: impossible\n", i);
} else {
printf("Case %d: %d\n", i, cnt);
}
}
}
return 0;
}

Problem D Division by 3
题目链接:Division by 3
题目分类:找规律
题目大意:给定a,b,求一个序列1,12,123……,12345678910,12345678911……从第a个数到第b个数有多少个数能被3整除
题目思路:通过3的整除性质找规律可以得知一下规律
if (i % 3 == 1) : Yes
else : No
将[1,b]满足题意得个数减去[1,a]满足题意的个数就是答案
AC代码:
#include <bits/stdc++.h>
using namespace std;
int sum[10] = {0, 0, 1};
int main() {
int t, a, b;
while (~scanf("%d", &t)) {
for (int i = 1; i <= t; i ++) {
scanf("%d %d", &a, &b);
a --;
int k1 = a / 3 * 2 + sum[a % 3];
int k2 = b / 3 * 2 + sum[b % 3];
printf("Case %d: %d\n", i, k2 - k1);
}
}
return 0;
}
Problem E Dice (I)
题目链接:Dice (I)
题目分类:动态规划
题目大意:有n个k面骰子,求有多少种摆法方式,使得朝上的点数之和为s
题目思路:其实这就是一个多重集组合数的问题,唯一的不同就是这题每个物品至少取一个,具体多重集组合数dp公式的证明留再dp专题再写
AC代码:
#include <bits/stdc++.h>
using namespace std;
const int mod = 1e8 + 7;
int dp[2][15001];//滚动数组优化
int main() {
int t, n, k, s;
while (~scanf("%d", &t)) {
for (int cc = 1; cc <= t; cc ++) {
scanf("%d %d %d", &n, &k, &s);
memset(dp, 0, sizeof(dp));
dp[0][0] = 1;
for (int i = 1; i <= n; i ++) {
dp[1][i] = 1;
for (int j = i + 1; j <= s; j ++) {
if (j - 1 - k >= 0) {//小心出现负数
dp[1][j] = (dp[1][j - 1] + dp[0][j - 1] - dp[0][j - 1 - k] + mod) % mod;
} else {
dp[1][j] = (dp[1][j - 1] + dp[0][j - 1]) % mod;
}
}
memcpy(dp[0], dp[1], sizeof(dp[1]));
memset(dp[1], 0, sizeof(dp[1]));
}
printf("Case %d: %d\n", cc, dp[0][s]);
}
}
return 0;
}

Problem F Goldbach’s Conjecture
题目链接:Goldbach’s Conjecture
题目分类:欧拉筛
题目大意:给定n,求n可以分解为多少个两个素数之和
题目思路:很简单的一题,直接暴力枚举,在小于x/2部分,如果有,cnt+=2,在等于x/2部分,如果有,cnt+=1。这里着重写一下欧拉筛的原理:保证每个合数只被最小的质因子筛去
for (int i = 2; i <= MAX; i ++) {
if (isprime[i]) {
prime.push_back(i);
}
for (int j = 0; j < prime.size() && i * prime[j] <= MAX; j ++) {
isprime[i * prime[j]] = false;
if (i % prime[j] == 0) {
break;
}
}
}
两个疑问
①怎么保证所有素数被筛,所有素数不被筛
一个合数数必定能拆成p×m的形式,其中p为最小素因子,m大于等于p,我们欧拉筛最外层循环的i就是m,内层就是枚举所有的小于等于m的素数,但由于p时最小的,在内层j到达p之前,一定不会提前退出循环,所以合数一定能被全部筛掉。而对于素数而言,由于prime数组里面没有1,所以一定不会被筛掉
②为什么一个合数只会被最小素数筛掉
假设一个数拆成p×m的形式,p此时不是最小的素因子,我们设q为最小素因子,若它能在p×m时被筛去,相当于此时外层循环的i等于m,但此时的j不能跑到p,因为q整除m,在内层j=q时就已经break掉了
AC代码:
#include <bits/stdc++.h>
using namespace std;
const int MAX_N = 1e7;
bitset<MAX_N + 1> isprime;
vector<int> prime;
void pre_process() {
isprime.set();
for (int i = 2; i <= MAX_N; i ++) {
if (isprime[i]) {
prime.push_back(i);
}
for (unsigned j = 0; j < prime.size() && i * prime[j] <= MAX_N; j ++) {
isprime[i * prime[j]] = false;
if (i % prime[j] == 0) {
break;
}
}
}
}
int main() {
int t, x;
pre_process();//欧拉筛
while (~scanf("%d", &t)) {
for (int i = 1; i <= t; i ++) {
int cnt = 0;
scanf("%d", &x);
for (unsigned j = 0; j < prime.size() && prime[j] <= x / 2; j ++) {
if (isprime[x - prime[j]]) {
++ cnt;
}
}
printf("Case %d: %d\n", i, cnt);
}
}
return 0;
}

Problem G Leading and Trailing
题目链接:Leading and Trailing
题目分类:数学
题目大意:给定n和k,求n的k次幂的前3位和后三位
题目思路:求后三位比较简单,就是一个快速幂的模板。求前三位就有一点技巧了,我们知道一个数一定可以写成10的q次幂的形式(q不一定是整数),p=x+y,其中x为整数部分,y为小数部分,我们用科学计数法理解a×10^n的话,x的值就等于n,10的y次幂就等于a,那么假如我们求一个数的第一位的话,那就是floor(10的y次幂),如果求前三位呢,很显然,我们把p拆成x+y,其中y的整数部分为2,求floor(10的y次幂)就是结果(太难解释了吧 )
AC代码:
#include <bits/stdc++.h>
using namespace std;
//求前三位
long long pre(long long n, long long k){
double a = k * log10(n);//cmath库的log底数默认是e
a = a - floor(a) + 2;
long long b = pow(10.0, a);
return b;
}
//求后三位
long long pro(long long n, long long k) {
long long res = 1;
while (k > 0) {
if (k & 1) {
res = res * n % 1000;
}
n = n * n % 1000;
k >>= 1;
}
return res;
}
int main() {
int t;
while (~scanf("%d", &t)) {
for(int i = 1; i <= t; i ++) {
long long n, k;
scanf("%lld %lld", &n, &k);
printf("Case %d: %03lld %03lld\n", i, pre(n, k), pro(n, k));
}
}
return 0;
}

Problem H Aladdin and the Flying Carpet
题目链接:Aladdin and the Flying Carpet
题目分类:约数个数公式
题目大意:给定两个数a,b,求c×d=a的整数二元组的个数,其中c>=b,d>=b,c!=d,(c,d)和(d,c)统计一次
题目思路:最开始想到暴力,不过看了过题人数,肯定会超时。我们先用约数个数公式求出所有的组数,然后暴力将[1,b)的约数去除掉即可,不过我感觉数据出的刁钻的话,这个方法也过不了,我看了测试数据,b都在100以内
AC代码:
#include <bits/stdc++.h>
using namespace std;
const int M = 1e6;
bitset<M + 1> isprime;
vector<int> prime;
void pre_process() {
isprime.set();
for (int i = 2; i <= M; i ++) {
if (isprime[i]) {
prime.push_back(i);
}
for (unsigned j = 0; j < prime.size() && i * prime[j] <= M; j ++) {
isprime[i * prime[j]] = false;
if (i % prime[j] == 0) {
break;
}
}
}
}
int main() {
int t;
long long a, b;
pre_process();//欧拉筛
while (~scanf("%d", &t)) {
for (int i = 1; i <= t; i ++) {
scanf("%lld %lld", &b, &a);
if (a * a >= b) {
printf("Case %d: 0\n", i);
} else {
long long ans = 1, x = b;
//质因数分解和约数个数公式
for (unsigned j = 0; j < prime.size() && prime[j] * prime[j] <= x; j ++) {
long long cnt = 0;
while (x % prime[j] == 0) {
cnt ++;
x /= prime[j];
}
ans *= (cnt + 1);
}
if (x != 1) {
ans *= 2;
}
ans /= 2;//只统计一次
long long cnt = 0;
//剔除小于a的约数
for (long long j = 1; j < a; j ++) {
if (b % j == 0) {
cnt ++;
}
}
printf("Case %d: %lld\n", i, ans - cnt);
}
}
}
return 0;
}

这题补充一下约数个数公式的证明
一个数约数的质因子一定是那个数的质因数
设x = p1 ^ c1 * p2 ^ c2 * ... * pn ^ cn
设y = p1 ^ s1 * p2 ^ s2 * ... * pn ^ sn
y是x的约数,那么s1<=c1,s2<=c2,…,sn<=cn,那么每个si有ci+1种可能,故x的约数个数为(c1+1)×(c2+1)×…×(cn+1)
Problem I Sigma Function
题目链接:Sigma Function
题目分类:约数和公式
题目大意:给定n,求1到n中有多少个数约数和为偶数
题目思路:我们先分析上面式子什么时候为偶数,很显然,有一项为偶数时,它整个式子就是偶数,但这很复杂,我们正难则反,考虑奇数,要求每一项为奇数时
我们将式子还原
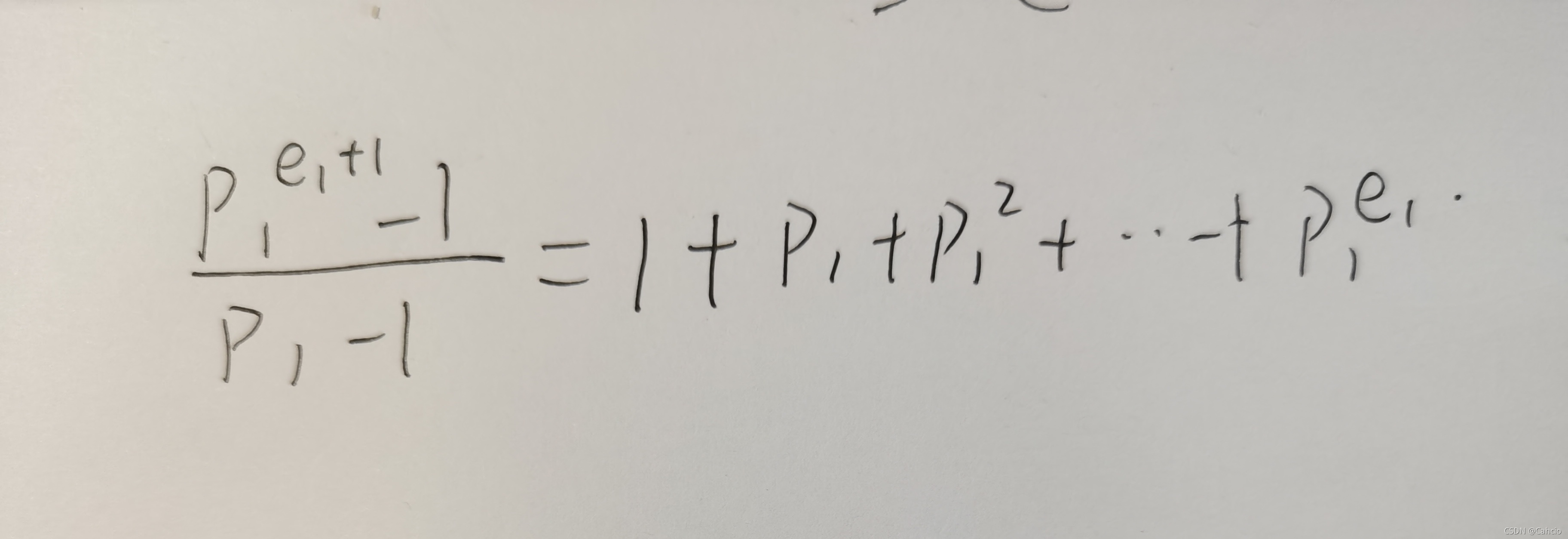
如果p是2的话,整个式子的一定是奇数,如果p是奇质数的话,式子的奇偶性取决于e1,e1一定要是偶数才能使得整个式子为奇数,下面分两种情况考虑,如果2的个数也是偶数的话,整个式子就是一个完全平方数,1到n的完全平方数个数为sqrt(n),如果2的个数为奇数呢,那么我们可以把一个2除过去,相当于求1到n/2的完全平方数个数
AC代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
LL pow2[40];
int main() {
LL n;
int t;
while (~scanf("%d", &t)) {
for (int j = 1; j <= t; j ++) {
scanf("%lld", &n);
printf("Case %d: %lld\n", j, n - (LL)sqrt(n) - (LL)sqrt(n / 2));
}
}
return 0;
}

自己的丑陋代码,没想到质数2的处理和快速求1到n的平方数个数
#include <bits/stdc++.h>
using namespace std;
long long pow2[40];
int main() {
long long n;
int t;
pow2[0] = 1;
for (int i = 1; i < 40; i ++) {
pow2[i] = (pow2[i - 1] << 1);
}
while (~scanf("%d", &t)) {
for (int j = 1; j <= t; j ++) {
scanf("%lld", &n);
long long cnt = 0, k;
for (long long i = 1; i * i <= n; i += 2) {
k = upper_bound(pow2, pow2 + 40, n / (i * i)) - pow2;
cnt += k;
}
printf("Case %d: %lld\n", j, n - cnt);
}
}
return 0;
}

通过分析法再结合约数个数公式的证明可以证明出约数和公式
Problem J Bi-shoe and Phi-shoe
题目链接:Bi-shoe and Phi-shoe
题目分类:欧拉函数
题目大意:给定n个数a1,a2……an,求欧拉函数f(bi)大于等于ai的bi的最小和
题目思路:其实就是求单个bi最小,然后加起来。我们证明一定是bi取素数时,最小,我们证明一个合数的欧拉函数值一定小于等于比它小且最接近它的素数的欧拉函数值,设合数为x,素数为p,由切比雪夫定理,p<x<2p,x最小素因子的最大值一定小于sqrt(x),那么f(x)<=x-x/sqrt(x)<=x-sqrt(x)<2p-sqrt§=p+p-sqrt§<=p-1=f§,根据我们证明的结论,我们就知道了一定是在取不小于ai+1的最近素数取到bi最小值
AC代码:注意MAX不能只开1e6
#include <bits/stdc++.h>
using namespace std;
const int MAX = 1e6 + 10;
bitset<MAX + 1>isprime;
void pre_process() {
isprime.set();
isprime[0] = isprime[1] = false;
for (int i = 2; i <= MAX; i ++) {
if (isprime[i]) {
for (int j = 2 * i; j <= MAX; j += i) {
isprime[j] = false;
}
}
}
}
int main() {
int n, t, x;
pre_process();//埃式筛,不想记prime组数
while (~scanf("%d", &t)) {
for (int j = 1; j <= t; j ++) {
scanf("%d", &n);
long long sum = 0;
for (int i = 0; i < n; i ++) {
scanf("%d", &x);
do {
x ++;
} while (!isprime[x]);
sum += x;
}
printf("Case %d: %lld Xukha\n", j, sum);
}
}
return 0;
}

借鉴博客:欧拉函数(详细证明+推导) 每日一遍,算法再见!
欧拉函数性质
性质1:如果n是质数,那么?(n) = n ? 1。证明显然
性质2:如果p是质数,那么?(pk) = pk - pk-1
1到pk中,只有p,2p……pk共有pk-1个数与之不互素,所以?(pk) = pk - pk-1
性质3:若a为质数,b mod a=0,?(a×b) = ?(b) ? a
a整除b,那么与a互质的数也与b互质,对于下面a个区间[1,b),[b,2b),…,[(a-1)b,ab),每个区间有?(b)个数与ab互质,所以?(a×b) = ?(b) ? a
性质4:若a,b互质,?(a×b) = ?(b) × ?(a),这个我不会证
性质5:对于任意正整数n,?(n)=n×(1-1/p1)×(1-1/p2)×…×(1-1/pn)
先将n质因数分解,然后结合性质2和性质4即可证明
模板
单个欧拉函数的计算
int euler(int x) {//通过性质5计算
int ans = x;
for (int i = 2; i * i <= x; i ++) {
if (x % i == 0) {
ans = ans * (i - 1) / i;
while (x % i == 0) {
x /= i;
}
}
}
return ans;
}
打表计算,这个好像要快一点
const int MAX = 1e6;
int phi[MAX + 1];
vector<int>prime;
bitset<MAX + 1>isprime;
void euler {
isprime.set();
isprime[0] = isprime[1] = true;
for (int i = 2; i <= MAX; i ++) {
if (isprime[i]) {
prime.push_back(i);
}
for (unsigned j = 0; j < prime.size() && i * prime[j] <= MAX; j ++) {
isprime[i * prime[j]] = false;
if (i % prime[j] == 0) {
phi[i * prime[j]] = prime[j] * i;//性质3
break;
} else {
phi[i * prime[j]] = (prime[j] - 1) * i;//性质4
}
}
}
}
Problem K Lcm与Gcd构造
题目链接:Lcm与Gcd构造
题目分类:最大公约数,最小公倍数
题目大意:给出2个数a,b的Gcd(最大公约数n)和Lcm(最小公倍数m),求所有符合条件的a,b中,a+b的最小值
题目思路:如果我们将Lcm除取Gcd,设为p,那么我们就是找c×d=p,c+d的最小值,因为c×Gcd=a,d×Gcd=b。根据均值不等式的性质,我们知道a与b相差越小,a+b越小,那么我们从sqrt p向前枚举,第一个满足题意的就是答案,也可以用动态规划写,时间快一倍
AC代码:也不知道为什么我之前写了dfs
#include <bits/stdc++.h>
using namespace std;
int gcd(int x, int y) {
return y ? gcd(y, x % y) : x;
}
int main() {
int t, d, m, ans;
while (~scanf("%d", &t)) {
while (t --) {
scanf("%d %d", &d, &m);
int n = m / d, k = sqrt(n);
for (int i = k; i >= 1; i --) {
if (n % i == 0 && gcd(i, n / i) == 1) {
ans = i + n / i;
break;
}
}
printf("%d\n", ans * d);
}
}
return 0;
}

动态规划(滚动数组又写错了 )
#include <bits/stdc++.h>
using namespace std;
vector<int> a;
bitset<40000> dp;
int main() {
int t, m, d, n;
while (~scanf("%d", &t)) {
while (t --) {
scanf("%d %d", &d, &m);
n = m / d;
a.clear();
for (int i = 2; i * i <= n; i ++) {
int power = 1;
while (n % i == 0) {
power *= i;
n /= i;
}
if (power != 1) {
a.push_back(power);
}
}
if (n != 1) {
a.push_back(n);
}
int sq = sqrt(m / d);
dp.reset();
dp[1] = true;
for (unsigned i = 0; i < a.size(); i ++) {
for (int j = sq; j >= 0; j --) {
if (dp[j] && j * a[i] <= sq) {
dp[j * a[i]] = true;
}
}
}
for (int k = sq; k >= 1; k --) {
if (dp[k]) {
printf("%d\n", k * d + m / k);
break;
}
}
}
}
return 0;
}

Problem L 数列求和
题目链接:数列求和
题目分类:mod的性质
题目大意:给出n和k,求1k+2k+3k+…nk 的和,由于结果太大,输出 mod 10007的结果。
题目思路: 这题之前在讲解之前没人做,都觉得n和k太大了,都能取到109。其实这是一道非常简单的题,因为mod的大小只是10007,那个和式,每过10007就会重复
AC代码:注意循环的处理
#include <bits/stdc++.h>
using namespace std;
const int MAX = 10007;
int ans[MAX + 1];
int fast_power(int base, int n, int mod = 10007) {
int res = 1;
while (n > 0) {
if (n & 1) {
res = res * base % mod;
}
base = base * base % mod;
n >>= 1;
}
return res;
}
void pre_process(int k) {
for (int i = 1; i <= MAX; i ++) {
ans[i] = (ans[i - 1] + fast_power(i, k)) % MAX;
}
}
int main() {
int t, n, k;
while (~scanf("%d", &t)) {
while (t --) {
scanf("%d %d", &n, &k);
pre_process(k);
printf("%d\n", n / MAX * ans[MAX] + ans[n % 10007]);
}
}
return 0;
}

Problem M 青蛙的约会
题目链接:青蛙的约会
题目分类:拓展欧几里得
题目大意:有一条长度为L的环路,两只青蛙分别从x点和y点沿同一方向跳跃,每次跳越花费时间相同但距离分别是m和n,问两只青蛙要跳跃多少次才能同一时间跳到同一个点上,若不存在则输出impossbile
题目思路:设经过时间t后,两只青蛙跳到同一个点上,所以(x + m × t)≡(y + n × t)mod L,所以t ×(n - m)+ k × l = x - y,这个很显然,就是一个不定方程的题目,用拓展欧几里得求解。我们下面来说明一下拓展欧几里得的原理,大致就是逆向的欧几里得算法,当b=0时,ax+by=d的一组解就是x=1,y=0,因为此时的a就是d,如果(a1,b1)是一组的系数,(x1,y1)是一组解,我们考虑如何推出它的上一层的解(x0,y0),我们知道,a1=b0,b1=a0%b0=a0-a0/b0×b0,代入a1x1+b1y1=c,得到a0y1+b0(x1-a0/b0×y1)=c,所以x0=y1,y0=(x1-a0/b0×y1)
AC代码:
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstdlib>
using namespace std;
//不能求出最小的x,再乘k
long long exgcd(long long a, long long b, long long &x, long long &y) {
long long d = a;
if (b != 0) {
d = exgcd(b, a % b, y, x);//通过传y,x化简
y -= (a / b) * x;
} else {
x = 1; y = 0;
}
return d;
}
int main() {
long long x, y, m, n, l, p, q;
while (~scanf("%lld %lld %lld %lld %lld", &x, &y, &m, &n, &l)) {
long long c = x - y, a = n - m;
long long d = exgcd(a, l, p, q);
if (c % d != 0) {
printf("Impossible\n");
} else {
l /= d;
//要保证t为正
printf("%lld\n", ((c / d * p) % l + l) % l);
}
}
return 0;
}
证明一下不定方程的结论,假设式子为ax+by=c,a和b的公约数为d,证明①ax+by=c的充要条件是(a,b)|c。必要性是显然的我们证明充分性。通过欧几里得算法能够找到一组m,n,使得mx+ny=d(其实这叫贝祖定律),那么我们同时乘以c/d,就能得到不定方程的解。②若(x0,y0)是该不定方程的解,则该不定方程所有的整数解为x=x0+b/d×t,y=y0-a/d×t。

Problem N Primes
题目链接:Primes
题目分类:素数判断
题目大意:给定一个数n,判断它是不是素数
题目思路:如果从2枚举到sqrt n,如果存在i,使得i整除n,则不是素数,否则是素数,证明一下,如果一个数n不是素数,则n=ab,a<=b,则a2<=n,a<=sqrt n,所以若一个数不是质数,一定存在一个小于sqrt n的数,使得它整除n。1和2要特判比较坑
AC代码:
#include <bits/stdc++.h>
using namespace std;
bool isprime(int x) {
for (int i = 2; i * i <= x; i ++) {
if (x % i == 0) {
return false;
}
}
return x != 1 && x != 2;
}
int main() {
int x, cnt = 1;
do {
scanf("%d", &x);
if (x <= 0) {
break;
}
if (isprime(x)) {
printf("%d: yes\n", cnt);
} else {
printf("%d: no\n", cnt);
}
cnt ++;
} while (1);
return 0;
}

Problem Maximum GCD
题目链接:Maximum GCD
题目分类:最大公约数,OI处理
题目大意:给定若干个数,要你求两两Gcd的最大值
题目思路:这题不是难在题求处理Gcd,而是输入的处理,一行不知道有多少个数,数之前还可能有多个空格(坑死我了 ),其实稍微注意一下,这题还是非常简单的
AC代码:
#include <bits/stdc++.h>
using namespace std;
//读入可能有多个空格
vector<int> a;
string s;
int gcd(int x, int y) {
return y ? gcd(y, x % y) : x;
}
int main() {
//freopen("in.txt", "r", stdin);
int t;
while (~scanf("%d\n", &t)) {
while (t --) {
a.clear();
getline(cin, s);//以换行符为终止符
string c;
for (unsigned i = 0; i < s.size(); i ++) {
if (s[i] == ' ') {//空格即为符号数字读完
if (c.size() != 0) {
a.push_back(stoi(c));//stoi,string转化为int
c.clear();
}
} else {
c += s[i];
}
}
if (c.size() != 0) {//剩余部分不要忘读了
a.push_back(stoi(c));
}
int d = 0;
//两两gcd
for (unsigned i = 0; i < a.size(); i ++) {
for (unsigned j = i + 1; j < a.size(); j ++) {
d = max(d, gcd(a[i], a[j]));
}
}
printf("%d\n", d);
}
}
return 0;
}

本次测试包含题目
跟测试的题目相比,训练的题目都太简单了
难度 ★★★ :1.Twice Equation 2.Lucky7
难度 ★★★★ :1.Coin Game 2.墨墨的等式
难度 ★★★★★ :1.Cowslip Collections 2.TreeDistance
Problem A Coin Game
题目链接:Coin Game
题目分类:互斥背包,贪心
题目大意:给定n和m,有n个机器,每个机器共有3枚金币,第i个机器第一次按得ai金币,第二次按得bi金币,第三次按得ai枚金币,设f(k)为按k次获得金币的最大值,求f(1)XORf(2)XOR…XORf(m)
题目思路:这个难度很大,第一次做大概率做不出来,我们把一个机器拆成价值为ai,重量为1①和价值为ai+bi,重量为2②的物品,按一次相当于取①,按两次相当于取②,按三次相当于取①和②。这题不能用动态规划做,因为状态实在太多,但是这个背包问题有个特点,就是物品重量只有两种状态1和2,我们想到贪心,从f(i)到f(i+1),要么是取一个价值最大的重量为1的物品,要么是丢弃一个重量为1,去一个价值最大的重量为2的物品(好像这也是动态规划 )。代码实现的话,先将两类物品从大到小排列,用两个指针指向当时取到的最大物品
AC代码:
#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long ULL;
const int MAX_N = 5e6;
const int MAX_M = 1.5e7;
constexpr int threshold = 10000000;
ULL a[MAX_N + 1], b[MAX_N + 1];
ULL n, m, k1, k2;
ULL xorShift128Plus() {
ULL k3 = k1,k4 = k2;
k1 = k4;
k3 ^= (k3 << 23);
k2 = k3 ^ k4 ^ (k3 >> 17) ^ (k4 >> 26);
return k2 + k4;
}
void gen() {
for(ULL i = 1;i <= n;i++) {
a[i] = xorShift128Plus() % threshold + 1;
b[i] = xorShift128Plus() % threshold + 1;
}
}
int main() {
while (~scanf("%llu %llu %llu %llu", &n, &m, &k1, &k2)) {
gen();
for (ULL i = 1; i <= n; i ++) {
b[i] += a[i];
}
sort(a + 1, a + n + 1, greater<ULL>());
sort(b + 1, b + n + 1, greater<ULL>());
ULL ans = 0, pa = 0, pb = 0, cur = 0;
for (ULL i = 1; i <= m; i ++) {
ULL cnt1 = 0, cnt2 = 0;
if (pa + 1 <= n) {//如果还有重量为1的物品没取完
cnt1 = a[pa + 1];
}
//如果手上有重量为1的物品且还有重量为2的物品没取完
if (pb + 1 <= n && pa > 0) {
cnt2 = b[pb + 1] - a[pa];
}
if (cnt1 >= cnt2) {
cur += cnt1;
pa ++;
} else {
cur += cnt2;
pb ++, pa --;
}
ans ^= cur;
}
printf("%llu\n", ans);
}
return 0;
}
Problem B Cowslip Collections(还没写呢)
题目链接:Cowslip Collections
Problem D 墨墨的等式
题目链接:墨墨的等式
题目分类:同余最短路,n元不定方程
题目大意:给定N、{an}、以及B的取值范围,求出有多少B可以使等式a1x1+a2y2+…+anxn=B存在非负整数解。
题目思路:一眼看下去,第一反应就是完全背包,不过这题的B实在是太大了,可以取到1012。对于求区间[l,r]中解的个数问题,我们的套路就是转化为[0,r]解的个数减去[0,l]解的个数,这题有个特点必须发现,假如B=x方程存在非负整数解,那么x+ai也一定存在非负整数解,那么我们取最小的ai(找其他的也行,不过就变得复杂了),设为mi,我们找到每个模0到mi-1的最小z,那么z+mi,z+2mi,…,都是可行的B,如何求最小的z呢,这就要用到同余最短路了,对每一个模mi的余数看成一个节点,把z看成最短距离。如何建边呢,我们知道B=0一定是模mi为0的最小z,所以起始点为0,dist[0]=0,我们可以通过使xi加1,将z转化到其他的z,相当于对y到(y+ai)模mi建一条权值为ai的边(z变大了ai),跑一个SPFA就能求得每个节点得最小z(若为INF则没有不存在)
AC代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int MAX_A = 5e5;
const LL INF = numeric_limits<LL>::max();
int n, a[12], k;
LL dist[MAX_A];
bool vis[MAX_A];//是否在队列
queue<int> que;
void spfa() {
fill(dist, dist + k, INF);
memset(vis, false, sizeof(vis));
dist[0] = 0;
vis[0] = true;
que.push(0);
while (!que.empty()) {
int v = que.front(); que.pop();
//反正n小,直接暴力找
for (int i = 0; i < n; i ++) {
int cur = (v + a[i]) % k;
if (dist[cur] > dist[v] + a[i]) {
dist[cur] = dist[v] + a[i];
if (!vis[cur]) {
que.push(cur);
vis[cur] = true;
}
}
}
vis[v] = false;
}
}
LL query(int i, LL x) {
if (dist[i] <= x) {
return (x - dist[i]) / k + 1;
}
return 0;
}
int main() {
LL l, r;
while (~scanf("%d %lld %lld", &n, &l, &r)) {
for (int i = 0; i < n; i ++) {
scanf("%d", &a[i]);
}
k = *min_element(a, a + n);
spfa();
LL res = 0;
for (int i = 0; i < k; i ++) {
res += query(i, r) - query(i, l - 1);
}
printf("%lld\n", res);
}
return 0;
}

Problem E Twice Equation
题目链接:Twice Equation
题目分类:佩尔方程,高精度
题目大意:求小大于等于L得最小n,使得2m(m+1)=n(n+1)有正整数解
题目思路: 恒等变形一下,(2n+1)2-2(2m+1)2=-1,这就是一个佩尔方程的题目,设x=2n+1,y=2m+1,求出x2-2y2=-1和x2-2y2=1的特价特解(1,1),(3,2),那么Xn=3Xn-1+4Yn-1,Yn=2Xn-1+3Yn-1
推荐博文:佩尔方程(超详细推导+例题讲解) 每日一遍,算法再见!
AC代码:
#include <bits/stdc++.h>
using namespace std;
int cur_x[200], cur_y[200], nex_x[200], nex_y[200];
int cur[200], ans[260][200], l;
char num[200];
void compute(int m, int n, int *a) {
int ma = max(cur_x[0], cur_y[0]);
for (int i = 1; i <= ma; i ++) {
a[i] = m * cur_x[i] + n * cur_y[i];
}
int k = 1;
for (k = 1; k <= ma || a[k]; k ++) {
a[k + 1] += a[k] / 10;
a[k] %= 10;
}
a[0] = k - 1;
}
void save_ans() {
nex_x[1] -= 1;
int k, sum = 0;
for (k = 1; k <= nex_x[0] && nex_x[k] < 0; k ++) {
nex_x[k] += 10;
nex_x[k + 1] -= 1;
}
l ++;
bool flag = true;
for (k = nex_x[0]; k >= 1; k --) {
sum = sum * 10 + nex_x[k];
if (sum >= 2) {
if (flag) {
ans[l][0] = k;
flag = false;
}
ans[l][k] = sum / 2;
sum %= 2;
}
}
}
void pre_process() {
cur_x[0] = cur_y[0] = cur_x[1] = cur_y[1] = 1;
while (ans[l][191] == 0) {
compute(3, 4, nex_x);
compute(2, 3, nex_y);
memcpy(cur_x, nex_x, sizeof(nex_x));
memcpy(cur_y, nex_y, sizeof(nex_y));
memset(nex_y, 0, sizeof(nex_y));
save_ans();
memset(nex_x, 0, sizeof(nex_x));
}
}
int cmp(int *a, int *b) {
if (a[0] != b[0]) {
return a[0] - b[0];
}
for (int i = a[0]; i >= 1; i --) {
if (a[i] != b[i]) {
return a[i] - b[i];
}
}
return 0;
}
void prt(int *a) {
for (int i = a[0]; i >= 1; i --) {
printf("%d", a[i]);
}
putchar(10);
}
int main() {
int t;
pre_process();
while (~scanf("%d", &t)) {
while (t --) {
scanf("%s", num);
int len = strlen(num), k = 1;
cur[0] = len;
for (int i = len - 1; i >= 0; i --) {
cur[k ++] = num[i] - '0';
}
for (int i = 1; i <= l; i ++) {
if (cmp(ans[i], cur) >= 0) {
prt(ans[i]);
break;
}
}
}
}
return 0;
}

Problem F Lucky7
题目链接:Lucky7
题目分类:中国剩余定理,快速乘,容斥原理
题目大意:给定x,y和n组二元组ai,bi,求x和y之间有多少个数满足能被7整除,但对任意的ai,模ai不余bi
题目思路:这放在数学上就是一道容斥原理的入门题
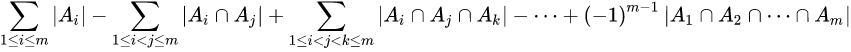
我们用容斥原理求出7整除的数中不满足题意数的个数,再用能被7整除的数的个数减去,就是答案了。逆元的求法可用扩展欧几里得,为了防止爆long long要用快速乘
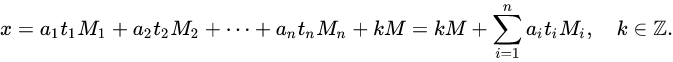
AC代码:
#include <bits/stdc++.h>
using namespace std;
long long a[15], b[15];
pair<long long, long long> c[11000][15], t[15];
int l, n;
//扩展欧几里得求数论倒数,
long long exgcd(long long a, long long b, long long &x, long long &y) {
long long d = a;
if (b != 0) {
d = exgcd(b, a % b, y, x);
y -= (a / b) * x;
} else {
x = 1, y = 0;
}
return d;
}
void dfs(int level, int cnt, int lms) {
if (cnt == lms) {
for (int i = 0; i < lms; i ++) {
c[l][i] = t[i];
}
l ++;
return ;
}
if (level == n) {
return ;
}
t[cnt] = {a[level], b[level]};
dfs(level + 1, cnt + 1, lms);
dfs(level + 1, cnt, lms);
}
//快速乘,和快速幂一样,就是乘换成了加
long long fast_prod(long long a, long long b, long long mod) {
long long res = 0;
while (b){
if (b & 1) res = (res + a) % mod;
a = (a + a) % mod;
b >>= 1;
}
return res;
}
int main() {
//freopen("in.txt", "r", stdin);
int t;
long long x, y;
while (~scanf("%d", &t)) {
for (int ct = 1; ct <= t; ct ++) {
scanf("%d %lld %lld", &n, &x, &y);
for (int i = 0; i < n; i ++) {
scanf("%lld %lld", &a[i], &b[i]);
}
long long ans = y / 7 - (x - 1) / 7;
for (int i = 1; i <= n; i ++) {//从1到n元组
l = 0;
dfs(0, 0, i);//dfs找到所有的i元组
long long num = 0;
for (int j = 0; j < l; j ++) {//对于所有的i元组
long long prod = 7;
for (int k = 0; k < i; k ++) {//先求M
prod *= c[j][k].first;
}
long long sum = 0;
for (int k = 0; k < i; k ++) {//i元组中每个数
long long q = -1, p = -1;
exgcd(prod / c[j][k].first, c[j][k].first, p, q);//p即为数论倒数,因为公约数为1
if (p < 0) {
p = c[j][k].first + p;
}
sum += fast_prod(fast_prod(c[j][k].second, p, prod), (prod / c[j][k].first), prod);
}
//[x,y]中模prod余sum的数的个数
//普遍的算法是,先算循环节的个数,每个循环节有一个
//再算不完整循环节中有没有满足的数
num += (y - sum) / prod - (x - sum - 1) / prod;
if (sum <= y && sum >= x) {
num ++;
}
}
if (i & 1) {
ans -= num;
} else {
ans += num;
}
}
printf("Case #%d: %lld\n", ct, ans);
}
}
return 0;
}

Problem F TreeDistance(还没做呢)
题目链接:TreeDistance