[数据结构与算法]前缀和的n个神奇操作

前情回顾

前缀和的基础用法戳这里—>传送门

众所周知，简单的前缀和解决的一般都是静态查询的问题，例如区间和、区间积等

操作的时候也很简单，就是根据需要来维护一个数组，每次查询的时候就用到tr[r] 与 tr[l - 1]这两个值来得出答案

例如：

A 智乃酱的区间乘积

题目描述：

给你一个长度为n的数组tr，m次查询，每次查询给你 l 和 r ，问tr[l] 乘到 tr[r] 后对1e9+7取模是多少

思路：

用到了取模，且查询的时候还涉及到了除法，所以要用逆元，而又因为模数是素数，所以可以用费马小定理求逆元

维护一个mul的前缀积数组，查询的时候就直接输出mul[r] * getniyuan(mul[l - 1])即可，getniyuan()是求逆元的函数

#include<map>
#include<set>
#include<stack>
#include<queue>
#include<cmath>
#include<bitset>
#include<cstdio>
#include<string>
#include<vector>
#include<sstream>
#include<cstring>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
using namespace std;

#define eps 1e-8
#define endl '\n'
#define inf 0x3f3f3f3f
#define MAX  100000 + 50
#define mod 1000000007
#define lowbit(x) (x & (-x))
#define sd(n) scanf("%lld",&n)
#define sdd(n,m) scanf("%lld %lld",&n,&m)
#define pd(n) printf("%d\n", (n))
#define pdd(n,m) printf("%d %d\n",n, m)
#define sddd(n,m,z) scanf("%d %d %d",&n,&m,&z)
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define mem(a,b) memset((a),(b),sizeof(a))
#define max(a,b) (((a)>(b)) ? (a):(b))
#define min(a,b) (((a)>(b)) ? (b):(a))

typedef  long long ll ;
typedef unsigned long long ull;
//不开longlong见祖宗!不看范围见祖宗!
inline int IntRead(){char ch = getchar();int s = 0, w = 1;while(ch < '0' || ch > '9'){if(ch == '-') w = -1;ch = getchar();}while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0';ch = getchar();}return s * w;}

int n, m;
ll x, l, r;
ll mul[MAX];

ll q_pow(ll a, ll b, ll MOD){
    ll ans = 1;
    while(b > 0){
        if(b & 1)ans = ans * a % MOD;
        a = a * a % MOD;
        b >>= 1;
    }
    return ans;
}

inline ll getniyuan(ll a, ll p){
    return q_pow(a, p - 2, p);
}

int main(){
    cin>>n>>m;
    mul[0] = 1;
    sd(mul[1]);
    for(int i = 2; i <= n; ++i){
        sd(x);
        mul[i] = mul[i - 1] * x % mod;
    }
    for(int i = 1; i <= m; ++i){
        sdd(l, r);
        ll ans = mul[r] * getniyuan(mul[l - 1], mod) % mod;
        cout<<ans<<endl;
        
    }
    return 0;
}

这只是前缀和的基础用法，接下来要讲的才是重头戏

“前缀和”的再定义！

广义的“前缀和”运算是指连续的进行若干次操作，产生一个叠加影响，且这种影响可以通过某种反向操作“撤销”。

比较常见的有满秩矩阵的乘积、前缀置换、卷积等

先讲解一下前缀置换是怎么回事

F牛牛的猜球游戏

题目描述：

给从0到9编号的十个球，原始状态是0，1，2……9，现在有n个交换操作，m次查询，查询的时候会给出l和r，每次查询的是球从最开始的状态，经过 l 到 r 的操作后的状态是什么

思路：

仔细想想，其实是符合广义的“前缀和”的定义的，我们要做的就是消除前 l 个球产生的影响

举个例子：

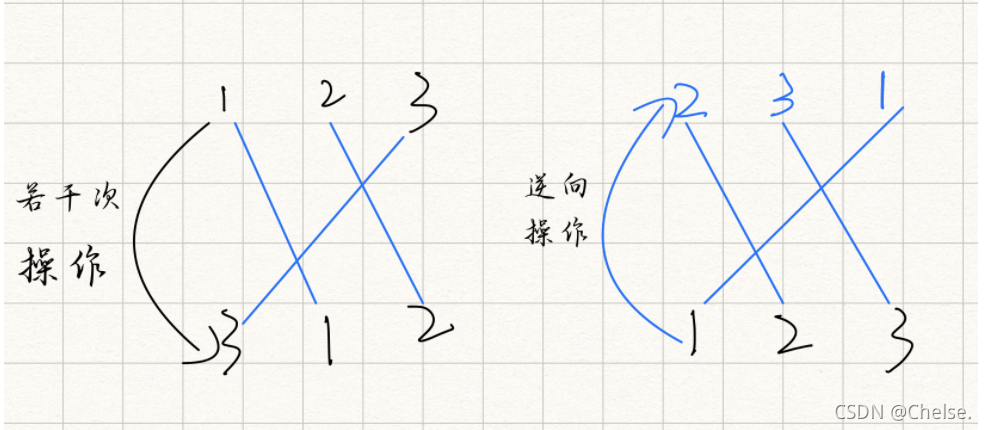
1 2 3 经过若干次操作得到3 1 2

而要消除3 1 2之前的操作，也就是要将3 1 2变成1 2 3，那就逆过来搞，这样如果我们要消掉3 1 2之前的操作，也就是相当于最开始是2 3 1的顺序。1 2 3对应r的顺序是可以得到的，那我们就可以根据2 3 1与1 2 3 的对应关系推出2 3 1开头时r的顺序，这就是我们要求得顺序，这就是广义的“前缀和”的思路，通过某些方法消除前 l 个产生的影响

#include<map>
#include<set>
#include<stack>
#include<queue>
#include<cmath>
#include<bitset>
#include<cstdio>
#include<string>
#include<vector>
#include<sstream>
#include<cstring>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
using namespace std;

#define eps 1e-8
#define endl '\n'
#define inf 0x3f3f3f3f
#define MAX  100000 + 50
#define mod 1000000007
#define lowbit(x) (x & (-x))
#define sd(n) scanf("%d",&n)
#define sdd(n,m) scanf("%d %d",&n,&m)
#define pd(n) printf("%d\n", (n))
#define pdd(n,m) printf("%d %d\n",n, m)
#define sddd(n,m,z) scanf("%d %d %d",&n,&m,&z)
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define mem(a,b) memset((a),(b),sizeof(a))
#define max(a,b) (((a)>(b)) ? (a):(b))
#define min(a,b) (((a)>(b)) ? (b):(a))

typedef  long long ll ;
typedef unsigned long long ull;
//不开longlong见祖宗!不看范围见祖宗!
inline int IntRead(){char ch = getchar();int s = 0, w = 1;while(ch < '0' || ch > '9'){if(ch == '-') w = -1;ch = getchar();}while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0';ch = getchar();}return s * w;}

int n, m, a, b, l, r;
int pos[MAX][10];
int tr[MAX][10];

int main(){
    sdd(n, m);
    for(int i = 0; i < 10; ++i)pos[0][i] = tr[0][i] = i;
    for(int i = 1; i <= n; ++i){
        sdd(a, b);
        for(int j = 0; j < 10; ++j){
            tr[i][j] = tr[i - 1][j];
            pos[i][j] = pos[i - 1][j];
        }
        swap(pos[i][tr[i][a]], pos[i][tr[i][b]]);
        swap(tr[i][a], tr[i][b]);
    }
    for(int i = 1; i <= m; ++i){
        sdd(l, r);
        for(int j = 0; j < 10; ++j){
            if(!j)cout<<pos[l - 1][tr[r][j]];
            else cout<<" "<<pos[l - 1][tr[r][j]];
        }
        cout<<endl;
    }
    return 0;
}

再讲讲“前缀和”和“满秩矩阵的乘积”的联系

首先，满秩矩阵A乘以满秩矩阵B，得到的矩阵必然是满秩的

证明: 因为A、B满秩，|A| > 0, |B| > 0, 而|AB| = |A| * |B| > 0, 所以AB是满秩的

其次，满秩矩阵A必然可逆

证明：因为A满秩，所以|A| > 0，即|A| != 0，所以必然可逆

所以，满秩矩阵可以用进行连乘，而通过逆矩阵撤销一部分的贡献，就可以获得特定部分(即[l, r])的贡献

E智乃酱的双塔问题

题目描述：

两座N层高的塔，每座塔内部的每一层都有的仅能向上的楼梯，此外，除了顶楼以外，每层都有一座连接两个高塔的楼梯，要么是左 i 连到右 i + 1，要么是右 i 连到左 i + 1，我们用’ / '表示第一种情况，用 ’ \ '表示第二种情况

现在你想知道从某座高塔的第hs层移动到第ht层的方案数

思路：

首先，映入脑海的是dp，假如每次都从第一层开始走，那肯定是用dp了，dp[i] [0] 表示到第 i 层的左侧的方案数，dp[i] [1]表示到第 i 层右侧的方案数

• dp[i] [0] = dp[i - 1] [0] + s[i - 1] == ’ \ ’ : dp[i - 1] [1] ? 0;
• dp[i] [1] = dp[i - 1] [1] + s[i - 1] == ’ / ’ ：dp[i - 1] [0] ? 0;

但是，这个题是从任意一层，任意一边开始，这样就不能用dp了，因为不满足无后效行的原则了，再看看“从某一层到另一层”显然是要用前缀和，但是how？简单的维护前缀和数字肯定不行，就像刚刚的dp一样是不对的，这时候就到了矩阵的用处了，我们使用矩阵连乘当作“前缀和”，消除影响时就可以用逆矩阵来消除

用两个二维矩阵分别代表两种有不同桥的层
a表示从该层左边到上面那层左边的方案数，b表示当前这层左边通过斜着的楼梯到右边的上面那层的方案数，c表示当前这层从右边通过斜着的左边的楼梯到达左边的那层的上面那层的方案数，d表示从当前这层的右边到上面那层的右边的方案数

所以如果是’ / '，就是x那样

如果是’ \ '，就是 y 那样

这样其实一个矩阵的四个点都是由两个转移而来，比如矩阵x * x，得到矩阵xx中的a是由x₁.a * x₂.a + x₁.c * x₂.a, 也就是左边的楼的第i层，可以由左边楼的i-1层直接上来，也可以从i-1层的右边斜着上来，和上面的dp方程不能说是一模一样，只能说是大差不离

这样按输入给的，就可以将矩阵连乘得到一个“前缀和”，每次查询的时候就再通过逆矩阵消除开始的那层的下面的所有层的影响即可

#include<bits/stdc++.h>
using namespace std;
const int MAX_MAT = 2;
const long long mod = 1e9 + 7;
struct Mat
{
	long long a[MAX_MAT][MAX_MAT];
	Mat()
	{
		for (int i = 0; i < MAX_MAT; ++i)
		{
			for (int j = 0; j < MAX_MAT; ++j)
			{
				a[i][j] = 0;
			}
		}
		for (int i = 0; i < MAX_MAT; ++i)
		{
			a[i][i] = 1;
		}
	}
	Mat(long long a1, long long a2, long long a3, long long a4)
	{
		a[0][0] = a1;
		a[0][1] = a2;
		a[1][0] = a3;
		a[1][1] = a4;
	}
};
long long quickpow(long long x, long long y, long long MOD = 9223372036854775807LL)
{
	long long ans = 1;
	while (y)
	{
		if (y & 1)
		{
			ans = (x * ans) % MOD;
		}
		x = (x * x) % MOD;
		y >>= 1;
	}
	return ans;
}
long long A[MAX_MAT][MAX_MAT << 1];
long long get_inv(long long x)
{
	return quickpow(x, mod - 2, mod);
}
void row_minus(int a, int b, long long k)
{
	for (int i = 0; i < 2 * MAX_MAT; ++i)
	{
		A[a][i] = (A[a][i] - A[b][i] * k % mod) % mod;
		if (A[a][i] < 0)A[a][i] += mod;
	}
	return;
}
void row_multiplies(int a, long long k)
{
	for (int i = 0; i < 2 * MAX_MAT; ++i)
	{
		A[a][i] = (A[a][i] * k) % mod;
	}
	return;
}
void row_swap(int a, int b)
{
	for (int i = 0; i < 2 * MAX_MAT; ++i)
	{
		swap(A[a][i], A[b][i]);
	}
}
Mat getinv(Mat x)
{
	memset(A, 0, sizeof(A));
	for (int i = 0; i < MAX_MAT; ++i)
	{
		for (int j = 0; j < MAX_MAT; ++j)
		{
			A[i][j] = x.a[i][j];
			A[i][MAX_MAT + j] = i == j;
		}
	}
	for (int i = 0; i < MAX_MAT; ++i)
	{
		if (!A[i][i])
		{
			for (int j = i + 1; j < MAX_MAT; ++j)
			{
				if (A[j][i])
				{
					row_swap(i, j);
					break;
				}
			}
		}
		row_multiplies(i, get_inv(A[i][i]));
		for (int j = i + 1; j < MAX_MAT; ++j)
		{
			row_minus(j, i, A[j][i]);
		}
	}
	for (int i = MAX_MAT - 1; i >= 0; --i)
	{
		for (int j = i - 1; j >= 0; --j)
		{
			row_minus(j, i, A[j][i]);
		}
	}
	Mat ret;
	for (int i = 0; i < MAX_MAT; ++i)
	{
		for (int j = 0; j < MAX_MAT; ++j)
		{
			ret.a[i][j] = A[i][MAX_MAT + j];
		}
	}
	return ret;
}
const int MAXN = 100005;
const Mat tA(1, 1, 0, 1);
const Mat tB(1, 0, 1, 1);
Mat operator * (Mat x, Mat y)
{
	Mat c;
	for (int i = 0; i < MAX_MAT; ++i) {
		for (int j = 0; j < MAX_MAT; ++j) {
			c.a[i][j] = 0;
		}
	}
	for (int i = 0; i < MAX_MAT; ++i) {
		for (int j = 0; j < MAX_MAT; ++j) {
			for (int k = 0; k < MAX_MAT; ++k) {
				c.a[i][j] = (c.a[i][j] + x.a[i][k] * y.a[k][j] % mod) % mod;
			}
		}
	}
	return c;
}
Mat presum[MAXN];
char s[MAXN];
int n, m, hs, ht, ps, pt;
int main()
{
	scanf("%d %d", &n, &m);
	scanf("%s", s + 1);
	presum[0] = Mat(1, 0, 0, 1);
	for (int i = 1; i < n; ++i)
	{
		if (s[i] == '/')
		{
			presum[i] = presum[i - 1] * tA;
		}
		else
		{
			presum[i] = presum[i - 1] * tB;
		}
	}
	while (m--)
	{
		scanf("%d %d %d %d", &hs, &ht, &ps, &pt);
		Mat ans = getinv(presum[hs - 1]) * presum[ht - 1];
		printf("%lld\n", ans.a[ps][pt]);
	}
	return 0;
}

多阶差分与多阶前缀和的引入

如果需要对区间进多次行加减操作，暴力跑肯定就不行，就需要引入差分来解决

//原数组
1 1 1 1 1 1 
//差分后
1 0 0 0 0 0 -1

如果需要对区间[l, r]+x，那就对差分数组的cha[l] += x, cha[r + 1] -= x即可，当所有的都修改完了，就可以通过一次前缀和获得修改后的数组，属实很方便

但是如果我要插入的是1 2 3 4 5 6… 这样的呢

//原数组
1 2 3 4 5 6 ...
//一次差分后
1 1 1 1 1 1 ...
//两次差分
1 0 0 0 0 0 ...

如果要插的是1 4 9 16 25 36……的呢

//原数组
1 4 9 16 25 36 ...
//一次差分
1 3 5 7 9 11 ...
//二次差分
1 2 2 2 2 2 ...
//三次差分
1 1 0 0 0 0...

是不是感觉有点东西了

看个例题：

H小w的糖果

题目描述：

三种操作

• 从pos位置开始往后，每个人发一个糖
• 从pos往后，每个人发前一个人数量+1的糖，第一个人发1个
• 从pos往后，按1 4 9 16……这样来发

思路：

三次差分，手推出来三种操作对第三次差分数组的影视是什么，然后去修改即可，最后求三次前缀和，输出即可

#include<map>
#include<set>
#include<stack>
#include<queue>
#include<cmath>
#include<bitset>
#include<cstdio>
#include<string>
#include<vector>
#include<sstream>
#include<cstring>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
using namespace std;

#define eps 1e-8
#define endl '\n'
#define inf 0x3f3f3f3f
#define MAX  100000 + 50
#define mod 1000000007
#define lowbit(x) (x & (-x))
#define sd(n) scanf("%d",&n)
#define sdd(n,m) scanf("%d %d",&n,&m)
#define pd(n) printf("%d\n", (n))
#define pdd(n,m) printf("%d %d\n",n, m)
#define sddd(n,m,z) scanf("%d %d %d",&n,&m,&z)
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define mem(a,b) memset((a),(b),sizeof(a))
#define max(a,b) (((a)>(b)) ? (a):(b))
#define min(a,b) (((a)>(b)) ? (b):(a))

typedef  long long ll ;
typedef unsigned long long ull;
//不开longlong见祖宗!不看范围见祖宗!
inline int IntRead(){char ch = getchar();int s = 0, w = 1;while(ch < '0' || ch > '9'){if(ch == '-') w = -1;ch = getchar();}while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0';ch = getchar();}return s * w;}

int t;
int n, m, op, l;
ll sum[MAX];

inline void presum(){
    for(int i = 1; i <= n; ++i){
        sum[i] += sum[i - 1];
        if(sum[i] > mod)sum[i] %= mod;
    }
}

int main(){
    sd(t);
    while (t--) {
        mem(sum, 0);
        sdd(n, m);
        for(int i = 1; i <= m; ++i){
            sdd(op, l);
            if(op == 1){
                ++sum[l];
                sum[l + 1] -= 2;
                ++sum[l + 2];
            }
            else if(op == 2){
                ++sum[l];
                --sum[l + 1];
            }
            else {
                ++sum[l];
                ++sum[l + 1];
            }
        }
        presum();
        presum();
        presum();
        for(int i = 1; i <= n; ++i)printf("%lld ", sum[i]);
        cout<<endl;
    }
    return 0;
}

NOIP2013积木大赛 NOIP2018道路铺设

题目描述：

这两个题不能说是毫无差别，只能说是一模一样

大概意思就是给你n个数，每次你可以选择一个区间使得区间的数-1，但不能减为负数，问所有数都变成0最少需要几次操作

思路：

这个题就直接贪心？

就直接求一次差分数组，跑一遍看，将所有的大于0的都加起来就是答案

为什么呢？因为如果差分数组tr[i] 大于0，说明前面一个一定比他小，我们就能把他们俩绑定起来一起削掉小的那部分，剩下的大的那部分 tr[i] 就得自己削，就会产生额外的操作次数tr[i]

#include<map>
#include<set>
#include<stack>
#include<queue>
#include<cmath>
#include<bitset>
#include<cstdio>
#include<string>
#include<vector>
#include<sstream>
#include<cstring>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
using namespace std;

#define eps 1e-8
#define endl '\n'
#define inf 0x3f3f3f3f
#define MAX  100000 + 50
#define mod 1000000007
#define lowbit(x) (x & (-x))
#define sd(n) scanf("%d",&n)
#define sdd(n,m) scanf("%d %d",&n,&m)
#define pd(n) printf("%d\n", (n))
#define pdd(n,m) printf("%d %d\n",n, m)
#define sddd(n,m,z) scanf("%d %d %d",&n,&m,&z)
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define mem(a,b) memset((a),(b),sizeof(a))
#define max(a,b) (((a)>(b)) ? (a):(b))
#define min(a,b) (((a)>(b)) ? (b):(a))

typedef  long long ll ;
typedef unsigned long long ull;
//不开longlong见祖宗!不看范围见祖宗!
inline int IntRead(){char ch = getchar();int s = 0, w = 1;while(ch < '0' || ch > '9'){if(ch == '-') w = -1;ch = getchar();}while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0';ch = getchar();}return s * w;}

int n, ans;
int tr[MAX];

int main(){
    sd(n);
    for(int i = 1; i <= n; ++i){
        sd(tr[i]);
        int d = tr[i] - tr[i - 1];
        if(d >= 1)ans += d;
    }
    cout<<ans<<endl;
    return 0;
}

G牛牛的Link Power I

题目描述：

给你一个01串，每一对(u, v)(满足s[u] = s[v] = 1,且v > u)会产生v - u + 1的价值，问你总价值是多少

思路：

这个题挺有意思的，先找个例子写出来就能发现一个好玩的东西，就是1对后面产生的价值是1 2 3 4……这样的，而这个东西我们刚刚讲了，可以用两次差分来解决的。

所以我们需要先把所有1的位置往后移一位，因为从1的后一位开始产生贡献

然后两次前缀和，再统计ans即可

1 0 0 0 1 0 0 1 0 1
  1 2 3 4 5 6 7 8 9  
          1 2 3 4 5
                1 2

#include<map>
#include<set>
#include<stack>
#include<queue>
#include<cmath>
#include<bitset>
#include<cstdio>
#include<string>
#include<vector>
#include<sstream>
#include<cstring>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
using namespace std;

#define eps 1e-8
#define endl '\n'
#define inf 0x3f3f3f3f
#define MAX  100000 + 50
#define mod 1000000007
#define lowbit(x) (x & (-x))
#define sd(n) scanf("%d",&n)
#define sdd(n,m) scanf("%d %d",&n,&m)
#define pd(n) printf("%d\n", (n))
#define pdd(n,m) printf("%d %d\n",n, m)
#define sddd(n,m,z) scanf("%d %d %d",&n,&m,&z)
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define mem(a,b) memset((a),(b),sizeof(a))
#define max(a,b) (((a)>(b)) ? (a):(b))
#define min(a,b) (((a)>(b)) ? (b):(a))

typedef  long long ll ;
typedef unsigned long long ull;
//不开longlong见祖宗!不看范围见祖宗!
inline int IntRead(){char ch = getchar();int s = 0, w = 1;while(ch < '0' || ch > '9'){if(ch == '-') w = -1;ch = getchar();}while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0';ch = getchar();}return s * w;}

int n;
string s;
ll tr[MAX];

int main(){
    sd(n);
    cin>>s;
    for(int i = 0; i < s.size(); ++i){
        if(s[i] == '1')tr[i + 1] = 1;
    }
    for(int i = 1; i <= n; ++i)tr[i] += tr[i - 1];
    for(int i = 1; i <= n; ++i)tr[i] += tr[i - 1];
    ll ans = 0;
    for(int i = 0; i < s.size(); ++i){
        if(s[i] == '1')ans += tr[i];
        ans %= mod;
    }
    
    cout<<ans<<endl;
    return 0;
}

上面一个是1 1 1 1…… ，一个是1 2 3 4 ……，一个是1 4 9 16……，这些其实没一个值都是由同一个多项式函数f(x)由不同的x求出来，第一个1 1 1 1是f(x) = 1；第二个1 2 3 4 是f(x) = x；第三个1 4 9 16是f(x) = x²,这样我们就发现了一个规律：假设f(x)中x的最高次数为p，那最少做p+1次差分就可以将任意长的区间修改变成一个p+1次的单点修改（是从 l 往后都修改，不存在 r 的情况），这就很有用了，我们来看一个例题：

D智乃酱的静态数组维护问题多项式

题目描述：

n个数，m次操作，每次会给一个k次多项式：f(x)=c₀x_k+c₁x_k?1+…+c_k?1x₁+c_k,以及一个区间[l,r]，然后你需要对a_l + f(1),a₂ + f(2)……依次类推，m次修改完了以后，有q次询问，每一次询问都是问[l, r]的区间元素和，答案对1e9+7取模

思路：

这个题看起来是不是就很狗了，没错，就是和狗

根据题目的范围k<=5，也就是说多项式最多时5次多项式，那我们最多就需要做6次差分，就能通过6次单点修改来代替

对于区间[l, r]，我们对于l是6次单点修改，那对于r也是6次单点修改，且r对应的那6个应该是负的，因为是要消除 l 对 r 后面产生的影响

#include<map>
#include<set>
#include<stack>
#include<queue>
#include<cmath>
#include<bitset>
#include<cstdio>
#include<string>
#include<vector>
#include<sstream>
#include<cstring>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
using namespace std;

#define eps 1e-8
#define endl '\n'
#define inf 0x3f3f3f3f
#define MAX  100000 + 50
#define mod 1000000007
#define lowbit(x) (x & (-x))
#define sd(n) scanf("%lld",&n)
#define sdd(n,m) scanf("%lld %lld",&n,&m)
#define pd(n) printf("%d\n", (n))
#define pdd(n,m) printf("%d %d\n",n, m)
#define sddd(n,m,z) scanf("%d %d %d",&n,&m,&z)
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define mem(a,b) memset((a),(b),sizeof(a))
#define max(a,b) (((a)>(b)) ? (a):(b))
#define min(a,b) (((a)>(b)) ? (b):(a))

typedef  long long ll ;
typedef unsigned long long ull;
//不开longlong见祖宗!不看范围见祖宗!
inline int IntRead(){char ch = getchar();int s = 0, w = 1;while(ch < '0' || ch > '9'){if(ch == '-') w = -1;ch = getchar();}while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0';ch = getchar();}return s * w;}

int n, m, q;
ll k, l, r;
ll tr[MAX];
ll cr[MAX];
ll ar[MAX], br[MAX];

inline void presum(ll tr[], ll len, ll k){
    while (k--) {
        for(int i = 1; i <= len; ++i){
            tr[i] += tr[i - 1];
            if(tr[i] >= mod)tr[i] %= mod;
        }
    }
}

inline void diff(ll tr[], ll len, ll k){
    while (k--) {
        for(ll i = len; i >= 1; --i){
            tr[i] -= tr[i - 1];
            while(tr[i] < 0)tr[i] += mod;
        }
    }
}

ll calc(ll x, ll cr[], ll k){
    ll ans = 0;
    ll cnt = 1;
    for(ll i = k; i >= 0; --i){
        ans += cr[i] * cnt % mod;
        if(ans >= mod)ans %= mod;
        cnt = cnt * x % mod;
    }
    return ans;
}

ll incalc(ll x, ll cr[], ll l, ll r, ll k){
    return (mod - calc(x + r - l + 1, cr, k)) % mod;
}

int main(){
    sddd(n, m, q);
    for(int i = 1; i <= n; ++i)sd(tr[i]);
    diff(tr, n, 6);
    while(m--){
        cin>>l>>r>>k;
        for(int i = 0; i <= k; ++i)sd(cr[i]);
        for(int i = 1; i <= 6; ++i){
            ar[i] = calc(i, cr, k);
            br[i] = incalc(i, cr, l, r, k);
        }

        diff(ar, 6, 6);
        diff(br, 6, 6);
        for(int i = 1; i <= 6; ++i){
            tr[l + i - 1] += ar[i];
            while(tr[l + i - 1] >= mod)tr[l + i - 1] -= mod;
            tr[r + i] += br[i];
            while(tr[r + i] >= mod)tr[r + i] -= mod;
        }
    }
    presum(tr, n, 7);
    while (q--) {
        sdd(l, r);
        cout<<((tr[r] - tr[l - 1]) % mod + mod) % mod<<endl;
    }
    return 0;
}

这才求6次差分-前缀和，还是不够屌，所以来个1e18的看看？

智乃酱的前缀和与差分

题目描述：

给你一个n个数的数组a，一个k

• k > 0 对a做k次前缀和，并输出
• k = 0 直接输出
• k < 0 对a做k次差分，并输出

输出的数可能很大，要模998244353

?10¹⁸≤k≤10¹⁸

思路：

这个题确实够恶心的，1e18次前缀和或1e18次的差分，根本没法求

不过我们观察一下多次前缀和是什么东西

1 1 1 1 1 1 1 
1 2 3 4 5 6 7 
1 3 6 10 15 21 28
1 4 10 20 35 56 84 
1 5 15 35 70 126 210
1 6 21 56 126 252 462
1 7 28 84 210 462 924 

显然啊，这是组合数对于第k行，其实就是$C_k^0{C}_{k+1}^1{C}_{k+2}^2\dots \dots$

这就可以用卷积来计算，嗯我不会，自己看代码吧

还有一个比较神奇的规律是取模数大于数组长度时，做k次前缀和存在循环节，长度就是mod，就可以根据这个性质来解决问题，其他的自己看代码吧，等我学了卷积再回来更

#include <cmath>
#include <cstring>
#include <algorithm>
#include <map>
#include <list>
#include <queue>
#include <vector>
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <deque>
using namespace std;
namespace NTT
{
const long long g = 3;
const long long p = 998244353;
long long wn[35];
long long pow2(long long a, long long b)
{
    long long res = 1;
    while (b)
    {
        if (b & 1) res = res * a % p;
        a = a * a % p;
        b >>= 1;
    }
    return res;
}
void getwn()
{
    for (int i = 0; i < 25; i++) wn[i] = pow2(g, (p - 1) / (1LL << i));
}
void ntt(long long *a, int len, int f)
{
    long long i, j = 0, t, k, w, id;
    for (i = 1; i < len - 1; i++)
    {
        for (t = len; j ^= t >>= 1, ~j & t;);
        if (i < j) swap(a[i], a[j]);
    }
    for (i = 1, id = 1; i < len; i <<= 1, id++)
    {
        t = i << 1;
        for (j = 0; j < len; j += t)
        {
            for (k = 0, w = 1; k < i; k++, w = w * wn[id] % p)
            {
                long long x = a[j + k], y = w * a[j + k + i] % p;
                a[j + k] = (x + y) % p;
                a[j + k + i] = (x - y + p) % p;
            }
        }
    }
    if (f)
    {
        for (i = 1, j = len - 1; i < j; i++, j--) swap(a[i], a[j]);
        long long inv = pow2(len, p - 2);
        for (i = 0; i < len; i++) a[i] = a[i] * inv % p;
    }
}
void mul(long long *a, long long *b, int l1, int l2)
{
    int len, i;
    for (len = 1; len <= l1 + l2; len <<= 1);
    for (i = l1 + 1; i <= len; i++) a[i] = 0;
    for (i = l2 + 1; i <= len; i++) b[i] = 0;
    ntt(a, len, 0); ntt(b, len, 0);
    for (i = 0; i < len; i++) a[i] = a[i] * b[i] % p;
    ntt(a, len, 1);
}
};
typedef long long ll;
#define _for(i,a,b) for(int i=(a) ;i<=(b) ;i++)
#define _rep(i,a,b) for(int i=(a) ;i>=(b) ;i--)
#define scd(v) scanf("%d",&v)
#define scdd(a,b) scanf("%d %d",&a,&b)
#define endl "\n"
#define IOS ios::sync_with_stdio(false)
#define pb push_back
#define all(v) v.begin(),v.end()
#define int long long
#define odd(x) x&1
#define mst(v,a) memset(v,a,sizeof(v))
#define lson p<<1 ,l,mid
#define rson p<<1|1,mid+1,r
#define ls p<<1
#define rs p<<1|1
#define fi first
#define se second
#define pii pair<double,double>
#define inf 0x7f7f7f7f
const int N=3e5+10;
const int mod=998244353;
int n,m,k;
int a[N];
int ni[N],ki[N];
void get_ni(int n)//O(n)拓展欧几求逆元
{
    ni[0] = ni[1]=1;//0和1逆元
    _for(i,2,n)
    {
        ni[i] = ((mod-mod/i)*ni[mod%i])%mod;
    }
    return;
}
void gei_ki(int k ,int len)//求组合数C(k,0) C(k+1,1) C(k+2,2)……
{
    k = (k%mod+mod)%mod;//某前缀和定理，mod>len时，做k次前缀和存在循环节
    ki[0]=1;
    _for(i,1,len-1)
    {
        ki[i] = ki[i-1] * ni[i]%mod * ((k-1+i)%mod )%mod;
    }
}
signed main()
{
    //!!//
//    freopen("data.txt","r",stdin);
    //!!
    IOS;
    NTT::getwn();
    get_ni(100000);
    
    cin>>n>>k;
    gei_ki(k,n);
    _for(i,0,n-1) cin>>a[i];//注意从第0项开始读入
    NTT::mul(a,ki,n,n);//ntt加速求a与系数ki的卷积
    _for(i,0,n-1)
    {
        cout<<a[i]<<" ";
    }
}

多维前缀和

相信大家对二维前缀和肯定不陌生

//dp[i][j]表示从(1,1)到(i,j)形成的矩形的元素和
dp[i][j] = dp[i][j - 1] + dp[i - 1][j] - dp[i - 1][j - 1] + tr[i][j]

这是利用简单的容斥原理实现的，但要是推广到三维、四维……n维，那就会麻烦的要死，容斥的项就有2ⁿ个，没法搞

但是还有另一种求二维前缀和的操作：

for(int i = 1; i <= n; ++i)
  for(int j = 1; j <= n; ++j)
    sum[i][j] += sum[i - 1][j];
for(int i = 1; i <= n; ++i)
  for(int j = 1; j <= n; ++j)
    sum[i][j] += sum[i][j - 1];

这是一种不利用容斥原理来实现的二维前缀和，主要思想是先一列列求，求完以后再一行行求

这种方法特别适合推广到多维前缀和，一维维的求，最后就得到前缀和

看个例子：

B智乃酱的子集与超集

题目描述：

n个物品，第i个物品的权值为a_i，对于一个物品集合U = {a_p1,a_p2,a_p3……a_pk},我们定义这个集合U的价值为a_p1⊕a_p2⊕a_p3⊕……⊕a_pk。即定义一个集合的价值为：该集合所拥有的物品权值之异或和

现在有m次询问，每次询问的时候会给你一个物品集合U，想知道这个U的所有子集的价值之和，以及所有超集的价值之和

思路：

乍一看是不是感觉和前缀和毛关系都没有，确实，这就是个状压dp，不过这里确实有前缀和的思想在里面，你可以把他看成n维的前缀和，n<=20，显然不能开一个20维的数组，那我们就可以用一个n位的二进制数表示出所有集合的情况，也就是状态压缩，其中每个数的每一位，0就代表这个位置的物品不选，1就代表选，就这样可以预处理出来所有集合的价值，相当于前缀和开始之前最开始的数组值。

然后就进行n次前缀和，这就是上面讲的一维维的去求和的过程，如果当前集合 j 的第 i 维是1，那就说明它有一个第 i 位是0的，其他位和j一样的集合，这就是是它的子集，会产生贡献，就加起来就行。如果当前集合 j 的第 i 维是0，就说明它有一个第 i 位是1的，其他位都是和j一样的集合，这就是它的超集，会对它产生贡献，加起来就行。

询问的时候就先造出来这个需要的数，然后就输出即可

#include<map>
#include<set>
#include<stack>
#include<queue>
#include<cmath>
#include<bitset>
#include<cstdio>
#include<string>
#include<vector>
#include<sstream>
#include<cstring>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
using namespace std;

#define eps 1e-8
#define endl '\n'
#define inf 0x3f3f3f3f
#define MAX  1048576
#define mod 1000000007
#define lowbit(x) (x & (-x))
#define sd(n) scanf("%lld",&n)
#define sdd(n,m) scanf("%d %d",&n,&m)
#define pd(n) printf("%d\n", (n))
#define pdd(n,m) printf("%d %d\n",n, m)
#define sddd(n,m,z) scanf("%d %d %d",&n,&m,&z)
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define mem(a,b) memset((a),(b),sizeof(a))
#define max(a,b) (((a)>(b)) ? (a):(b))
#define min(a,b) (((a)>(b)) ? (b):(a))

typedef  long long ll ;
typedef unsigned long long ull;
//不开longlong见祖宗!不看范围见祖宗!
inline int IntRead(){char ch = getchar();int s = 0, w = 1;while(ch < '0' || ch > '9'){if(ch == '-') w = -1;ch = getchar();}while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0';ch = getchar();}return s * w;}

int n, m;
int maxbit;
ll k, x;
ll tr[MAX];
ll pre[MAX];
ll suf[MAX];


int main(){
    sdd(n, m);
    maxbit = 1 << n;
    for(int i = 0; i < n; ++i)sd(tr[i]);
    for(int i = 0; i < maxbit; ++i){
        ll sum = 0;
        for(int j = 0; j < n; ++j){
            if(i & (1 << j))sum ^= tr[j];
        }
        pre[i] = suf[i] = sum;
    }
    for(int i = 0; i < n; ++i){
        for(int j = 0; j < maxbit; ++j){
            if(j & (1 << i))pre[j] += pre[j ^ (1 << i)];
            else suf[j] += suf[j ^ (1 << i)];
        }
    }
    while (m--) {
        sd(k);
        ll q = 0;
        for(int i = 0; i < k; ++i){
            sd(x);
            q |= (1 << (x - 1));
        }
        cout<<pre[q]<<' '<<suf[q]<<endl;
    }
    return 0;
}

思维导图（bushi