?前言?：

算法是一个程序员的内功，能很好的体现程序员的编程思维，通过学习和掌握常见的算法，不仅能提高coding能力，还能更加容易在笔面试中脱颖而出。本专栏将记录博主刷算法题的过程，不定期的会更新一些优质的算法题。如果对大家有帮助，别忘了三连支持哟！

?前言?：

?冒泡排序的思想?

💎具体思路形象化比喻💎

?💎冒泡排序的图解💎

?具体代码展示?

?时间复杂度的计算?

?冒泡排序的思想?

冒泡排序可以说是排序算法中最基础，最简单的，但是它的比较与交换思想确是十分值得借鉴的。

💎具体思路形象化比喻💎

💡：当我们要把10个数字进行冒泡排序时，我们可以这样思考该问题，把问题转化为有10个人来比武，我们该如何确定其武力的高低呢？我们可以采用打擂台的方法（为了方便描述问题，给这10个人编号为0至9），我们先假设0号武力最强，让他当擂主守擂，然后1~9号不服，因此我们让1~9号依次上擂台比武，若0号赢了说明其有实力，让他继续打后面的人，若输了则代表0号没有实力，则让赢的人当擂主继续接受后面人的挑战。这样下来最后站在擂台上的一定是所有人中实力最强的，则给他第一名的奖牌，让他去观战。然后我们重复该思路在剩余9个人中，决出最强者，拿到第二名的奖牌，以此类推，当第九轮时我们将发放第九名的奖牌，这时1~9名都已经确定了，那么剩下的那个人一定是第十名。所以我们有这样的规律，n个人比武我们最多比n-1轮。

💡：?读到这里大家可能还有疑惑为什么n个人最多是n-1轮呢？少于n-1轮的情况是怎么出现的？这个问题先放在这里，等看完图解后相信大家会明白很多。

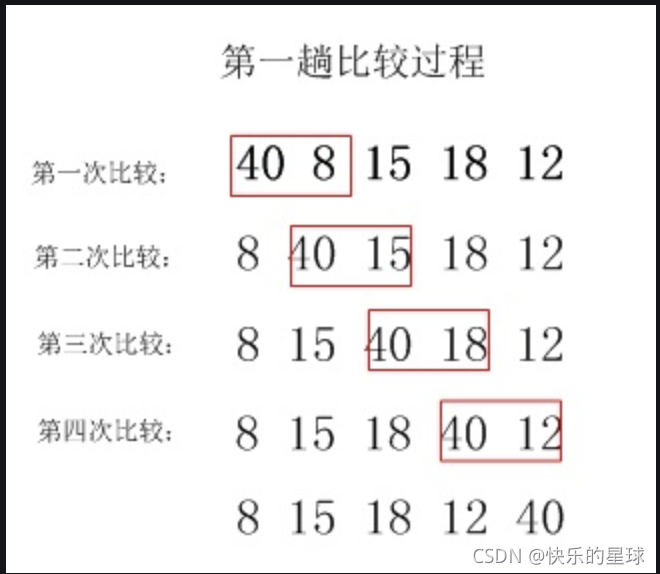
?💎冒泡排序的图解💎

🔑：图例：（该图片转载至网络图库）

?从之前的讲述中我们由打擂思想可以知道每一趟比较都会把最大值放到最右边，从这个图中我们可以看到先假设第一个数最大，然后让它和后面的一个数比较，如果大就交换位置，如果小了，就让大的那个代替它去争最大值，继续往后比较，而且由图可知每一次比较都是相邻元素进行比较，并且保证每一次相邻元素的右边那个必定是较大的数。

至于为什么n个数最多是n-1次，这种最多的情况是在每一个元素都错位的基础上（意思是每一个元素在一开始的位置和最终有序的位置不一致，即目标升序，开始降序），那么我们就要在0~n-1范围上通过上述方法把最大值放在n-1位置上，再在0~n-2范围上重复该操作，依次类推，因为所有数都是错位的所以每一次比较都是必要的，那每一次操作均不可以少，所以是n-1次。

如果我们假设10个数中有5个数的位置开始就已经正确了，所以我们只需要在剩下的5个数中进行上述思想把最大值放到这5个错位的位置的最右边，这样只要4次就足够让这10个数有序。

所以我们可以总结出以下规律，n个数最多进行n-1趟，实际进行次数是（错位数的数目-1）.

?具体代码展示?

void Swap(int arr[], int i, int j)
{
	//交换法1
	int tmp = arr[i];
	arr[i] = arr[j];
	arr[j] = tmp;
	//交换法2
	//arr[i] = arr[i] ^ arr[j];
	//arr[j] = arr[i] ^ arr[j];
	//arr[j] = arr[i] ^ arr[j];
}
void bubuleSort(int arr[], int sz)
{
	for (int i = sz - 1; i > 0; i--)
	{
		int flag = 0;//假设每一趟进来时都没有排序完
		for (int j = 0; j < i; j++)
		{
			if (arr[j] > arr[j + 1])
			{
				flag = 1;
				Swap(arr,j,j+1);//冒泡排序本质是相邻元素比较大的向右送
			}
		}
		if (flag == 0)//如果一次过后flag=0说明这一趟没有交换，所有数已经拍好序
		{
			break;
		}
	}
}