[数据结构与算法]你还不懂红黑树删除？看这篇就够了！！！硬淦红黑树---彻底拿下它！！！

前言:在开始之前，先给大家推荐一个网站，这个网站就是红黑树的插入，删除实现网站，你只需要手动输入要插入或删除的结点，网站自动帮你调整红黑树，非常方便！！！可以帮你验证你的红黑树操作是否正确

红黑树操作网站请点击这里！！！

红黑树：红黑树是一种特殊的二插查找数，不过为了防止二插查找树在最差情况下蜕变成链表，因此红黑树利用了结点的颜色来调节树的平衡，这使得红黑树的任意一条路径长度都不可能超过其他路径的两倍，因此红黑树是一种自调节的高度平衡的二叉查找树。

性质

• 性质1：结点要么是红要么是黑
• 性质2：根节点必须是黑色
• 性质3：每个叶子节点（NIL）是黑色
• 性质4：每个红色节点的两个子节点一定都是黑色。，不能有两个红色节点相连
• 性质5：从根节点开始，到这条路径上的空节点，各条路径上的黑色结点个数相同

推论：根据以上五个性质，我们可以有以下推论

• 推论1：如果结点是红色，那么其父亲（如果有）和儿子一定是黑色
• 推论2：如果结点是黑色，那么他的孩子和父亲可能是空色或者黑色
• 推论3：如果结点是黑色，并且有一个非空的黑色孩子，那么该结点的另一个孩子一定不是空
• 推论4：红黑树的任意一条路径长度都不可能超过其他路径的两倍

红黑树删除讨论：要删除一个结点，我们知道，这个要删除的结点要么是根节点，要么不是根节点，要么是红色结点，要么不是红色结点。基于此，那么这个结点可能的情况有如下几种

1 删除的是根节点
2 删除的非根节点
3 删除的是黑色结点
4 删除的是红色结点

以上四种情况包括了所有可能删除的情况，可是如果仅仅根据上面这种分类方法就想写出一颗红黑树的删除操作是不太现实的，因此必须对以上四种情况进行细分。

删除结点的讨论：关于要删除的结点，我们知道，这个结点要么有两个孩子，要么有一个孩子，要么无孩子，情况如下

1删除的结点有两个孩子
2 删除的结点有一个孩子
3 删除的结点无孩子

我们先思考一个问题，对于删除的结点，是没有孩子简单，还是有一个孩子简单，还是无孩子简单？(这里暂时先不考虑红黑色结点的颜色)

答案显而易见，对于没有孩子的结点，我们直接删除，操作就结束了，对于有一个孩子的结点，我们将删除结点的父节点重新指向该孩子，操作也就结束了，而当有两个孩子时，如果我们执行操作将会很复杂，因为有两个孩子，当删除该结点时，删除结点的父节点该指向删除结点的哪个孩子呢？

因此，对于以上问题，我们对于BST的删除（红黑树也是一种BST）有一种原则，就是对有两个孩子的结点进行装换，转换成只有一个孩子或者没有孩子结点，这种转换就是将要删除结点的左子树的最大值替换要删除结点的值，然后真正要删除的就是刚刚左子树的最大值那个结点（也可以用右子树的最小值来替换，结果都一样，这里红黑树的删除统一使用左子树的最大值来替换删除结点）：如下图所示
这里我们假设要删除结点7，由于7结点有两个孩子，那么我们找7结点左子树的最大来替换，从上图我们可以看出7结点左子树的最大值是5。因此我们使用5来更新7结点的值，然后删除5结点，如下图所示：

对于上面经过替换操作之后，我们真正要删除的结点要么只有一个孩子，要么无孩子。

下面我们开始正式讨论红黑树的删除操作
我们在上面对于红黑树的删除操作分了几种情况，但是还不够详细，不利于我们写代码，下面我们就详细的对于红黑树的删除操作进行拆分。

分析：对于红黑树的删除，进行细分，可大致分为以下几种情况，在这里我们先列出所有的情况，然后再对每一种情况进行详细的解释（建议每种情况参照着下面的解释来看）

1 如果删除的是根节点

1.1如果根节点无孩子：删除根节点，根节点指向空，结束
1.2如果根节点有一个孩子：删除根节点，孩子成为新根，孩子颜色变黑，结束

2 如果删除的不是根节点

2.1如果删除的是红结点：删除红色结点，结束
2.2如果删除的是黑结点

2.2.1如果黑结点有一个孩子：黑结点的父亲指向孩子并且孩子的父指针链接父亲，孩子变黑，删除黑结点，结束
2.2.2如果黑色结点无孩子

2.2.2.1如果兄弟结点是红色：父亲变红，兄弟变黑

2.2.2.1.1如果兄弟是父亲的左：以父亲为支点右旋，更新结点信息，重新判断
2.2.2.1.2如果兄弟是父亲的右：以父亲为支点左旋，更新结点信息，重新判断

2.2.2.2如果兄弟结点是黑色

2.2.2.2.1如果兄弟是父亲的左

2.2.2.2.1.1如果左侄子红：兄弟变为父亲的颜色，父亲变黑，侄子变黑，以父亲为支点右旋，结束
2.2.2.2.1.2如果右侄子红：兄弟变红，右侄子变黑，以兄弟为支点左旋，更新结点信息，重新判断
2.2.2.2.1.3如果两个侄子全黑

2.2.2.2.1.3.1如果父亲红：兄弟变红，父亲变黑，结束
2.2.2.2.1.3.2如果父亲黑：兄弟变红，父亲为新Z，重新判断

2.2.2.2.2如果兄弟是父亲的右

2.2.2.2.2.1如果左侄子红右侄子空：兄弟变红色，左侄子变黑色，以兄弟为支点右旋，更新结点信息，重新判断
2.2.2.2.2.2如果右侄子红：兄弟变父色，父亲变黑，右侄子变黑，以父亲为支点左旋，结束
2.2.2.2.2.3如果两个侄子全黑（即兄弟无孩子，侄子全是空）

2.2.2.2.2.3.1如果父亲红：兄弟变红，父亲变黑，结束
2.2.2.2.2.3.2如果父亲黑：兄弟变红，父亲为新Z，重新判断

情况分析（注：这里所讨论的要删除的结点都是转换后实际要删除的结点，实际要删除的结点只能有一个或者无孩子，上面已经叙述过）

情况1：如果删除的是根节点

首先对于删除的是根节点的情况，那么所删除的根节点要么是红，要么是黑，并且可能有一个孩子或者无孩子，因此1下面所包含的几种情况包含了所有删除是根的情况。下面进一步分析：

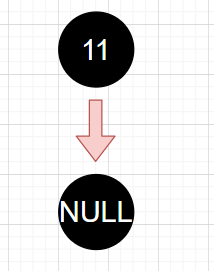
1.1：如果根节点无孩子：删除根节点，根节点指向空，结束（删除11）

对于这种情况，由于删除的根无孩子，因此直接删除就行，不做赘述，操作结束

1.2如果根节点有一个孩子：删除根节点，孩子成为新根，孩子颜色变黑，结束（删除11）

对于这种情况，删除的是根节点，并且根节点有一个孩子。由于根节点只有一个孩子，那么这个孩子一定是红色的！为什么这个结点的颜色一定是红色的呢？首先我们想一下红黑树的性质5，各条路径上的黑色结点相同。由于根节点只有一个孩子，如果这个孩子的颜色是黑色，并且没有兄弟，显然这个红黑树的黑色结点数是不相等的。
因此，对于这种情况，我们在这里我们将根节点删除，并把孩子颜色变黑（根节点必须是黑色），操作结束

上面两种情况就是删除的是根节点的情况，并不复杂，红黑树的删除真正复杂的地方在于下面这种情况！非根节点的删除！！！（这里再提一下，我们所讨论的结点是经过转换过得，只有一个孩子或者无孩子！！！）

情况2：如果删除的不是根节点（后续图片只列出一种情况，不全部列出了，都很类似）

上面讨论过了所有对于根节点的删除，因此情况1之外的所有情况就是对于非根结点的删除。对于非根结点的删除，同样，可能删除的结点有一个孩子或者无孩子，可能删除的结点是红色结点或者是黑色结点，这包含了所有的情况，我们由简入深，一步步分析。

2.1如果删除的是红结点：删除红色结点，结束（删除3）

首先，如果我们删除的是红色结点，那么红色结点一定无孩子！为什么红色结点无孩子呢？我们知道，红色结点如果有孩子，那么必须孩子必须是黑色的，并且如果要有黑色的孩子，必须得同时有两个黑孩子，而我们经过转换后，所要删除的结点最多只能有一个孩子。因此，如果删除的是红色结点，那么该红色结点一定是叶子结点。因此，直接将红色叶子结点删除即可，结束。

2.2如果删除的是黑结点

如果不是红色结点，那么删除的一定就是黑色结点。
如果删除的是黑色结点，那么兄弟一定不为空！
为什么兄弟一定不为空呢？
假设兄弟是空，那么删除之前，要删除黑色结点的这条路径就比其兄弟结点的路径多黑结点，即黑结点个数一定不相等。因此，如果删除的是黑结点，那么兄弟一定存在（为什么我们这里要强调兄弟一定存在呢，这是因为为了保证后面我们获取兄弟结点时一定能获取到！！！）

2.2.1如果黑结点有一个孩子：黑结点的父亲指向孩子，并链接孩子的父指针，孩子变黑，删除黑结点，结束（删除5）

如果黑色结点有一个孩子，那么这个孩子一定是红色！为什么孩子一定是红色呢？如果该黑色结点的孩子时黑色，那么同样，也肯定是有两个孩子，而经过我们转换之后，最多只能有一个孩子。如果该孩子时黑色，那么此树肯定不平衡。因此，该黑色删除结点的孩子一定是红色，删除红色结点不影响黑色结点的个数。因此，我们直接将该红色结点删除即可，结束。

2.2.2如果黑色结点无孩子

黑色结点有孩子的情况讨论完了，下面再讨论无孩子的情况。对于黑色结点无孩子时，由于删除的是黑色结点，因此我们就得想办法从兄弟结点来借一个黑色结点来保持平衡，那么这种情况我们必须得考虑兄弟结点的情况。另外，兄弟结点颜色的不同，也会导致情况不同，因此我们需要详细的讨论兄弟结点的颜色问题。

2.2.2.1如果兄弟结点是红色：父亲变红，兄弟变黑

如果兄弟结点的颜色是红色，那么此时父亲和侄子结点的颜色一定是黑色，因为红黑树不允许两个红色结点相连。对于此种情况，我们要将父亲变红，兄弟变黑，然后以父亲为支点旋转。由于要考虑是左旋还是右旋，我们要考虑兄弟是父亲的左还是右。

2.2.2.1.1如果兄弟是父亲的左：以父亲为支点右旋，更新结点信息，重新判断（删除10）

此种情况下，删除结点10，显然10结点无孩子，并且其兄弟为红色，由于要删除的结点颜色为红色，且兄弟结点颜色是红色，那么兄弟结点必然有两个孩子。为什么兄弟结点一定有两个孩子呢？如果兄弟结点没有两个孩子，首先因为兄弟结点的颜色是红色，这条兄弟结点的分支就少了一个黑色结点，如果该兄弟结点没有孩子或者只有一个孩子，那么肯定不会达到平衡。现在我们知道了兄弟结点一定有两个孩子，并且这两个孩子一定是黑孩子（兄弟是红，不允许有两个红节点相连），那我们在进行变色再进行右旋后，旋转后的结果如下图所示。由于发生了旋转，因此在我们旋转完成之后，我们需要重新更新父子兄弟关系，由于之前的结点已经删除，所以在更新兄弟结点的关系时我们通过判断父亲节点来找出兄弟结点。从旋转后的图像可以看出，经过旋转后，兄弟结点仍为8，且是父亲的左，而此时兄弟结点是黑色，父亲节点是红色，即将删除情况转换情况 ：删除结点为黑色结点且无孩子，父亲红，兄弟黑这种情况,因此，我们需要重新判断

2.2.2.1.2如果兄弟是父亲的右：以父亲为支点左旋，更新结点信息，重新判断（删除3）

由于要删除节点3，并且3是黑色且无孩子。因此，当把节点3删去之后该条路径一定会少一个黑色节点；如果想让黑色节点个数相同，那么我们此时就需要将兄弟的红色节点借过来，使得该条路径和其他路径的黑色节点个数相同。
那么我们要如何把兄弟的红色节点借过来呢？
如果想把兄弟的黑色节点借过来，那么我们必须要进行旋转，在这里我们需要进行左旋。由于父亲节点是黑色，如果直接进行左旋的话兄弟这条路径就会少一个黑色结点，这不是我们想要的。因此，如果我们不想让兄弟路径在旋转之后黑色节点个数减少，那么我就需要将黑色节点作为这两条路径的公共节点（其他情况同）。因此，在旋转之前我们要先将父亲节点变红，兄弟结点变黑，然后以父亲节点为支点左旋，左旋之后，兄弟结点就是公共节点，两条路径上的黑色结点个数并没有发生变化，并且此时红色结点已经在少黑色结点的这条路径上了。从旋转后的图像可以看出，经过旋转后，兄弟结点为8，且是父亲的右，而此时兄弟结点是黑色，父亲节点是红色，即将删除情况转换情况 ：删除结点为黑色结点且无孩子，父亲红，兄弟黑这种情况,因此，我们需要重新判断

小总结：对于兄弟结点是红色的情况，经过变换后我们总是能转换成兄弟结点是黑色且父亲节点是红色的情况

2.2.2.2如果兄弟结点是黑色

对于如果兄弟的结点颜色如果是黑色这种情况，就非常复杂了，我们从下面的讨论情况也能看出来。因为如果兄弟结点是黑色，那么其父亲可能是红色或者黑色，兄弟结点的儿子也可能是红色或者黑色。我们一步步讨论。
下面这两种情况：如果兄弟是父亲的左与如果兄弟是父亲的右两种情况基本相同，这里只对兄弟是父亲的右进行讨论，另一种情况就请您自己类比一下吧，基本上是一样。

2.2.2.2.1如果兄弟是父亲的左

2.2.2.2.1.1如果左侄子红：兄弟变为父亲的颜色，父亲变黑，侄子变黑，以父亲为支点右旋，结束

2.2.2.2.1.2如果右侄子红：兄弟变红，右侄子变黑，以兄弟为支点左旋，重新判断

2.2.2.2.1.3如果两个侄子全黑

2.2.2.2.1.3.1如果父亲红：兄弟变红，父亲变黑，结束
2.2.2.2.1.3.2如果父亲黑：兄弟变红，父亲为新Z，重新判断

2.2.2.2.2如果兄弟是父亲的右

2.2.2.2.2.1如果左侄子红右侄子空：兄弟变红，左侄子变黑，以兄弟为支点右旋，重新判断（删除3）

如果左侄子红，右侄子空，此种情况下我们想将左侄子这个红色结点转移到原先删除的位置来补充缺少的黑色结点。然而我们不能直接左旋，如果直接进行左旋，那么兄弟结点的左孩子将直接跑到另一个路径，将导致兄弟路径缺少黑色结点。因此，在进行左旋之前，我们要首先以兄弟结点进行右旋，来防止兄弟路径结点减少。在进行右旋之后，我们发现此时兄弟结点为黑，兄弟的右侄子为红，这是我们所讨论的其中一种情况，因此我们重新判断即可，如下图：

2.2.2.2.2.2如果右侄子红：兄弟变父色，父亲变黑，右侄子变黑，以父亲为支点左旋，结束

这里只考虑了右侄子是否为红，并没有考虑左侄子是红还是空，这和上面那种情况（即左侄子红右侄子空）这种情况有点区别啊，为什么呢？这里之所以不考虑左值子的情况，是因为只要右侄子存在，左侄子就不影响红黑树调整平衡。为什么不影响呢？我们想一下，这里兄弟是父亲的右，在删除结点3之后，如果我们想调整平衡，那么我们必须要以进行左旋。在进行左旋时，由于父亲节点7的颜色不确定（因为兄弟是黑结点），如果想旋转之后路径上的黑色结点个数保持不变，那么我们就需要将这个不确定的结点仍然作为路径的公共节点，左旋之后兄弟节点9就成为公共节点，因此我们就需要将兄弟节点的颜色变成父亲节点的颜色，然后将父亲节点颜色变成黑色，再以父亲为支点进行左旋。如果此时兄弟结点9的右孩子为空，左旋之后如下所示：

显然，旋转后结点9的右侧这条路径少一个黑色结点，树不平衡，因此我们需要考虑兄弟节点的右孩子是否为空这种情况。另外，我们同样可以看出，经过左旋之后，兄弟节点的左孩子最后一定会成为叶子结点（或者为空），这显然不会影响路径的长度（我们需要知道，如果兄弟节点的一个孩子为红，那么另一个孩子要么是空要么是红节点，自己可以试着分析一下，并不难）
因此，如果右侄子是红节点，我们需要将兄弟变父色，父亲变黑，右侄子变黑，然后以父亲为支点左旋，结束（如下图）

2.2.2.2.2.3如果两个侄子全黑

2.2.2.2.2.3.1如果父亲红：兄弟变红，父亲变黑，结束

对于此种情况，删除结点是黑且无孩子，且兄弟是黑，两个侄子全黑，此种情况我们无法从兄弟这里借结点，因为兄弟这里的结点颜色全部是黑色。然而，我们发现父亲节点的颜色是红色，我们想了是不是只要将父亲节点编程黑色就行了呢？父亲节点变成黑色的话那么删除的那条路径就会多出一个黑色结点，这确实没错，可是在那条路径多出黑色结点的同时，兄弟这条路径也多出了一个黑色结点，因此我们在将父亲节点变成黑色的同时也需要将兄弟结点的颜色变成红色。

2.2.2.2.2.3.2如果父亲黑：兄弟变红，父亲为新Z，重新判断

对于此种情况，我们肯定不能想着将父亲节点变成黑色了，因为父亲节点本身就是黑色，那么我们需要怎么做呢？既然向兄弟借不了，那么我们只能去找父亲借了，我们同样将兄弟变成红色（保证下面是平衡的），然后令父亲节点为“删除”的哪个节点（注意：这里的删除是假装要删除的结点，即假装要删除的结点是少黑色结点的，由于这个位置少黑色结点，因此我们就需要向其他人借结点了），更新结点关系后重新判断。

总结

至此，红黑树的所有删除操作已经结束，确实情况有点多哈。真的所有删除情况都考虑了嘛？难道你说都考虑了就是都考虑了吗？确实都已经考虑了，下面我们再整体分析一下为什么所有的情况都考虑了。
我们知道，我们要删除的结点要么是根要么不是根，我们在一开始就对删除的是根的情况进行了分析，即把所有删除的是根的情况都考虑了。接着我们就对删除的情况非根进行了考虑。删除的是跟和非根，这两种情况互补，合一起就是所有的情况。接着我们就对删除非根的情况进一步分析。由于一个删除的结点要么是红色要么是黑色，我们先对删除的结点是红色的进行了考虑，然后对删除的结点是黑色进行了考虑，这两种情况也是互补的，因此也包括了所有的情况。然后对于删除结点是红色的情况我们分析，红色结点直接删除。接着又对删除节点是黑色的进行了讨论，如果删除结点是黑色的，我们讨论了黑色结点是有一个孩子还是没有孩子，由于在进行实际的删除操作之前我们进行转换，即将所有的删除结点有两个孩子的情况转换为实际要删除的结点最多有一个孩子的情况。显然对于删除情况为有一个孩子和无孩子进行了讨论也涵盖了所有情况。接着对于删除结点无孩子时，我们又对兄弟结点进行了讨论。兄弟结点显然也只可能有红色和黑色，即对兄弟结点红色和黑色的讨论也包含了所有情况。对兄弟结点是红色时，我们分析了兄弟是父亲的左或者右来判断是左旋还是右旋，同样包含了所有情况。对兄弟结点是黑色时，由于此时父亲结点可能是红色和黑色，侄子可能是红色和黑色，我们又对父亲结点是红色，父亲节点是黑色，侄子红，侄子黑等情况进行了讨论。这些所有的讨论都是封闭的，即使基于上一种情况互补的讨论，因此这些情况涵盖了所有删除操作的情况。

代码实现

#include <stdio.h>
#include <stdlib.h>
enum COLOR{RED,BLACK};
typedef struct tree
{
	int nValue;
	enum COLOR color; 
	struct tree *pfather;
	struct tree *plchild;
	struct tree *prchild;
}BinaryTree;

void RightRotaryTree(BinaryTree *pTree,BinaryTree **pRoot)
{
	if(pTree == NULL || pTree->plchild == NULL) return;

	BinaryTree *pRotaryChild = pTree->plchild;
	BinaryTree *pRotaryGS = pTree->plchild->prchild;
	BinaryTree *pRotaryFather = pTree->pfather;
	//旋转的点的左孩子重新连接
	pTree->plchild = pRotaryGS;
	if(pRotaryGS != NULL)
	{
		pRotaryGS->pfather = pTree;
	}
	//旋转点的左孩子
	pRotaryChild->prchild = pTree;
	pTree->pfather = pRotaryChild;
	//如果有父亲，连接旋转点的父亲
	pRotaryChild->pfather = pRotaryFather;
	if(pRotaryFather != NULL)
	{
		if(pRotaryFather->plchild == pTree)
		{
			pRotaryFather->plchild = pRotaryChild;
		}
		else
		{
			pRotaryFather->prchild = pRotaryChild;
		}
	}
	else//旋转的是根节点时换根
	{
		*pRoot = pRotaryChild;
	}
}
void LeftRotaryTree(BinaryTree *pTree,BinaryTree **pRoot)
{
	if(pTree == NULL || pTree->prchild == NULL) return;

	BinaryTree *pRotaryChild = pTree->prchild;
	BinaryTree *pRotaryGS = pTree->prchild->plchild;
	BinaryTree *pRotaryFather = pTree->pfather;
	//旋转的点的左孩子重新连接
	pTree->prchild = pRotaryGS;
	if(pRotaryGS != NULL)
	{
		pRotaryGS->pfather = pTree;
	}
	//旋转点的左孩子
	pRotaryChild->plchild = pTree;
	pTree->pfather = pRotaryChild;
	//如果有父亲，连接旋转点的父亲
	pRotaryChild->pfather = pRotaryFather;
	if(pRotaryFather != NULL)
	{
		if(pRotaryFather->plchild == pTree)
		{
			pRotaryFather->plchild = pRotaryChild;
		}
		else
		{
			pRotaryFather->prchild = pRotaryChild;
		}
	}
	else//旋转的是根节点时换根
	{
		*pRoot = pRotaryChild;
	}
}
BinaryTree* SearchNode(BinaryTree *pRoot,int nValue)
{
	if(pRoot == NULL) return NULL;

	BinaryTree *pFather = pRoot;
	BinaryTree *pNode = pRoot;
	while(pFather)
	{
		pNode = pFather;
		if(pFather->nValue < nValue && pFather->prchild)
			pFather = pFather->prchild;
		else if(pFather->nValue > nValue)
			pFather = pFather->plchild;
		else
			return pFather;
	}
	return pNode;
}
//获取叔叔节点
BinaryTree *GetUncle(BinaryTree *pFather)
{
	BinaryTree *pGrandFather = pFather->pfather;
	if(pGrandFather == NULL)
		return NULL;
	else if(pGrandFather->plchild == pFather)
		return pGrandFather->prchild;
	else
		return pGrandFather->plchild;
}
//获取兄弟节点
BinaryTree *GetBrother(BinaryTree *pFather,BinaryTree *pNode)
{
	return pFather->plchild != pNode ? pFather->plchild : pFather->prchild;
}
//插入红黑树的节点
void InsertRBTNode(BinaryTree *pTree,BinaryTree **pRoot,int nValue)//Z为新插入的节点
{
	//为新插入的节点申请空间
	BinaryTree *pTemp = (BinaryTree*)malloc(sizeof(BinaryTree));
	pTemp->color = RED;
	pTemp->nValue = nValue;
	pTemp->plchild = NULL;
	pTemp->prchild = NULL;
	pTemp->pfather = NULL;

	//树为空：直接插入，并且根变黑
	if(*pRoot == NULL)
	{
		*pRoot = pTemp;
		(*pRoot)->color = BLACK;
		return;
	}
	//查找插入节点位置
	BinaryTree *pFather = SearchNode(*pRoot,nValue);
	//如果插入的节点相同
	if(pFather->nValue == nValue)
		return;
	//直接插入
	if(nValue < pFather->nValue)
		pFather->plchild = pTemp;
	else
		pFather->prchild = pTemp;
	//链接父亲
	pTemp->pfather = pFather;

	//父亲节点是黑色：结束
	if(pFather->color == BLACK)
		return;
	//父亲节点是红色
	BinaryTree *pGrandFather = pFather->pfather;
	BinaryTree *pUncle = GetUncle(pFather);
	while(pFather->color == RED)
	{
		//叔叔红：父变黑，叔叔变黑，爷爷变红，爷爷为新Z，爷爷非根重新判断
		if(pUncle && pUncle->color == RED)
		{
			pFather->color = BLACK;
			pUncle->color = BLACK;
			pGrandFather->color = RED;
			pTemp = pGrandFather;
			//如果爷爷是根
			if(pTemp == *pRoot)
			{
				pTemp->color = BLACK;
				return;
			}
			//更新父子关系
			pFather = pTemp->pfather;
			pUncle = GetUncle(pFather);
			pGrandFather = pFather->pfather;

			continue;
		}
		//叔叔黑（叔叔黑才发生旋转，另外叔叔黑可能是空）
		else
		{
			//爷爷为空:父亲变黑，结束
			if(pGrandFather == NULL)
			{
				pFather->color = BLACK;
				return;
			}
			//爷爷非空
			else
			{
				//父亲是爷爷的左
				if(pFather == pGrandFather->plchild)
				{
					//Z是父亲的左：爷爷变红，父亲变黑，爷爷为支点右旋，结束
					if(pTemp == pFather->plchild)
					{
						pGrandFather->color = RED;
						pFather->color = BLACK;
						RightRotaryTree(pGrandFather,pRoot);
						return;
					}
					//Z是父亲的右：父为新Z，父为支点左旋，重新判断
					else
					{
						pTemp = pFather;
						LeftRotaryTree(pTemp,pRoot);
						//更新父子关系
						pFather = pTemp->pfather;
						pGrandFather = pFather->pfather;
						pUncle = GetUncle(pFather);
						continue;
					}
				}
				//父亲是爷爷的右
				else
				{
					//Z是父亲的左：父为新Z，父为支点右旋，重新判断
					if(pTemp == pFather->plchild)
					{
						pTemp = pFather;
						RightRotaryTree(pTemp,pRoot);
						//更新父子关系
						pFather = pTemp->pfather;
						pGrandFather = pFather->pfather;
						pUncle = GetUncle(pFather);
						continue;
					}
					//Z是父亲的右：爷爷变红，父亲变黑，爷爷为支点左旋，结束
					else
					{
						pGrandFather->color = RED;
						pFather->color = BLACK;
						LeftRotaryTree(pGrandFather,pRoot);
						return;
					}
				}
			}
		}
	}
}

//删除节点
void DeleteRBTNode(BinaryTree *pTree,BinaryTree **pRoot,int nValue)
{
	if(*pRoot == NULL) return;
	//查找要删除的节点，并转换（真正要删除的只有一个孩子或无孩子）
	BinaryTree *pNode = SearchNode(pTree,nValue);
	BinaryTree *pMark = pNode;//标记要删除的节点
	//如果没找到，则直接返回
	if(pNode == NULL || pNode->nValue != nValue)
	{
		printf("There don't have the nValue int the tree.\n");
		return;
	}
	//如果找到了则将节点转换：转换成真正要删除的节点
	BinaryTree *pFather = pNode->pfather;
	//寻找左边最右替换删除节点
	if(pNode->plchild && pNode->prchild)//有两个孩子才进行转换
	{
		pNode = pNode->plchild;
		while(pNode->prchild)
			pNode = pNode->prchild;
		pMark->nValue = pNode->nValue;
	}
	//如果删除的是根
	if((*pRoot)->nValue == nValue)
	{
		//如果根无孩子：直接删除，结束
		if((*pRoot)->plchild == NULL && (*pRoot)->prchild == NULL)
		{
			free(*pRoot);
			*pRoot = NULL;
			return;
		}
		//如果根有一个孩子：直接删除，红孩子成为新根，根变黑，结束
		if(((*pRoot)->plchild == NULL && (*pRoot)->prchild != NULL) || ((*pRoot)->plchild != NULL && (*pRoot)->prchild == NULL))
		{
			BinaryTree *pDel = *pRoot;
			*pRoot = (*pRoot)->plchild == NULL? (*pRoot)->prchild:(*pRoot)->plchild;
			(*pRoot)->color = BLACK;
			(*pRoot)->pfather = NULL;
			free(pDel);
			pDel = NULL;
			return;
		}
	}
	//-----------下面删除的是非根的情况-------------------（因为上面判断的就是删除的是根的情况，因此走下来就一定是非根）
	//如果删除的是红节点：直接删除，父亲指向空，结束
	pFather = pNode->pfather;
	//printf("pFather[%d]\n",pFather->nValue);
	if(pNode->color == RED)
	{
		if(pFather->plchild == pNode)
			pFather->plchild = NULL;
		else 
			pFather->prchild = NULL;

		printf("pNode[%d]\n",pNode->nValue);
		free(pNode);
		pNode = NULL;
		return;
	}
	//如果删除的非根且是黑节点
	else
	{
		//有一个孩子：直接删除，孩子颜色变黑，爷爷指向孙子，结束
		if(pNode->plchild != NULL)
		{
			if(pFather->plchild == pNode)
				pFather->plchild = pNode->plchild;
			else
				pFather->prchild = pNode->plchild;

			pNode->plchild->pfather = pFather;
			pNode->plchild->color = BLACK;

			free(pNode);
			pNode = NULL;
			return;
		}
		else if(pNode->prchild != NULL)
		{
			if(pFather->plchild == pNode)
				pFather->plchild = pNode->prchild;
			else
				pFather->prchild = pNode->plchild;

			pNode->prchild->pfather = pFather;
			pNode->prchild->color = BLACK;

			free(pNode);
			pNode = NULL;
			return;
		}
		//无孩子
		else
		{
			//首先将节点删除
			if(pFather->plchild == pNode)
				pFather->plchild = NULL;
			else
				pFather->prchild = NULL;

			free(pNode);
			pNode = NULL;
			//获取兄弟节点
			BinaryTree *pBrother = GetBrother(pFather,pNode);
			while(1)
			{
				//如果兄弟是红节点
				if(pBrother->color == RED)
				{
					//如果兄弟是父亲的右：父变红，兄弟变黑，以父亲为支点左旋，更新节点信息，重新判断
					if(pBrother == pFather->prchild)
					{
						pFather->color = RED;
						pBrother->color = BLACK;
						LeftRotaryTree(pFather,pRoot);
						pBrother = GetBrother(pFather,pNode);
						continue;
					}
					//如果兄弟是父亲的左：父变红，兄弟变黑，以父亲为支点右旋，更新节点信息，重新判断
					else
					{
							printf("11 左红右空[%d]\n",pBrother->nValue);
						pFather->color = RED;
						pBrother->color = BLACK;
						RightRotaryTree(pFather,pRoot);
						pBrother = GetBrother(pFather,pNode);
						continue;
					}
				}
				//如果兄弟是黑节点
				else
				{
					//如果兄弟是父亲的右
					if(pBrother == pFather->prchild)
					{
						//如果左侄子红右侄子空：兄弟变红，左侄子变黑，以兄弟为支点右旋,更新节点信息，重新判断
						if(pBrother->plchild && pBrother->plchild->color == RED && pBrother->prchild == NULL)
						{
							pBrother->color = RED;
							pBrother->plchild->color = BLACK;
							RightRotaryTree(pBrother,pRoot);

							//更新节点关系
							pBrother = GetBrother(pFather,pNode);
							continue;
						}
						//如果右侄子红：兄弟变父色，父亲变黑，右侄子变黑，以父亲为支点左旋，结束
						else if(pBrother->prchild && pBrother->prchild->color == RED)
						{
							pBrother->color = pFather->color;
							pFather->color = BLACK;
							pBrother->prchild->color = BLACK;
							LeftRotaryTree(pFather,pRoot);

							return;
						}
						//如果俩侄子全黑
						else
						{
							//如果父亲红：兄弟变红，父为变黑，结束
							if(pFather->color == RED)
							{
								pBrother->color = RED;
								pFather->color = BLACK;

								return;
							}
							//如果父亲黑：兄弟变红，父为新Z，重新判断（Z指代要“删除”的节点）
							else
							{
								pBrother->color = RED;
								pNode = pFather;
								//如果此时pNode 为根，则将根变黑，结束
								if(pNode == *pRoot)
								{
									pNode->color = BLACK;
									return;
								}
								pFather = pNode->pfather;
								pBrother = GetBrother(pFather,pNode);

								continue;
							}
						}
					}			
					//如果兄弟是父亲的左
					else
					{
						//如果左侄子红：兄弟变为父亲的颜色，父亲变黑，左侄子变黑，以父亲为支点右旋，结束
						if(pBrother->plchild && pBrother->plchild->color == RED)
						{
							pBrother->color = pFather->color;
							pBrother->plchild->color = BLACK;
							pBrother->plchild->color = BLACK;
							RightRotaryTree(pFather,pRoot);

							return;
						}
						//如果右侄子红左侄子空：兄弟变红，右侄子变黑，以兄弟为支点左旋，更新节点信息，重新判断
						else if(pBrother->plchild == NULL && pBrother->prchild && pBrother->prchild->color == RED)
						{
							pBrother->color = RED;
							pBrother->prchild->color = BLACK;
							LeftRotaryTree(pBrother,pRoot);
							//更新节点信息
							pBrother = GetBrother(pFather,pNode);
							continue;
						}
						//如果俩侄子全黑
						else
						{
							//如果父亲红：兄弟变红，父为变黑，结束
							if(pFather->color == RED)
							{
							printf("7 左红右空[%d]\n",pBrother->nValue);
								pBrother->color = RED;
								pFather->color = BLACK;

								return;
							}
							//如果父亲黑：兄弟变红，父为新Z，重新判断(Z指代要“删除”的节点)
							else
							{
								pBrother->color = RED;
								pNode = pFather;
								//如果此时pNode 为根，则将根变黑，结束
								if(pNode == *pRoot)
								{
									pNode->color = BLACK;
									return;
								}
								pFather = pNode->pfather;
								pBrother = GetBrother(pFather,pNode);

								continue;
							}
						}
					}
				}
			}
		}
	}
}
//创建RBT
void CreateRBT(BinaryTree **pTree)
{
	//添加节点
	printf("please input node value (0 is quit)\n");
	int nValue;
	//while(scanf("%d",&nValue) && nValue)
	int arr[] = {20,11,9,3,1,6,10,16,14,18,19,36,28,23,33,30,49,58};
	int nLen = sizeof(arr)/sizeof(arr[0]);
	for(int i = 0;i < nLen;i++)
	{
		InsertRBTNode(*pTree,pTree,arr[i]);
		//printf("please input node value (0 is quit)\n");
	}
}
//中序遍历
void MidOrderTree(BinaryTree *pTree)
{
	if(pTree == NULL) return;

	MidOrderTree(pTree->plchild);
	printf("nValue[%d]\t color[%d]\n",pTree->nValue,pTree->color);
	MidOrderTree(pTree->prchild);

}
//前序遍历
void FrontOrderTree(BinaryTree *pTree)
{
	if(pTree == NULL) return;

	printf("nValue[%d]\t color[%d]\n",pTree->nValue,pTree->color);
	FrontOrderTree(pTree->plchild);
	FrontOrderTree(pTree->prchild);

}
int main()
{
	BinaryTree *pTree = NULL;

	CreateRBT(&pTree);
	printf("Create the tree is\n");
	MidOrderTree(pTree);

	int select = 0;;
	int nValue = 0;
	while(select != -1)
	{
		printf("\nPlease select DeleteNode or InsertNode:0 InsertNode  1 DeleteNode  -1 Quit\n");
		scanf("%d",&select);
		if(select == 0)
		{
			printf("\nPlease input InsertNode nValue\n");
			scanf("%d",&nValue);
			InsertRBTNode(pTree,&pTree,nValue);
			printf("\nAfter InsertNode ther Node[%d],ther MideReverse\n",nValue);
			MidOrderTree(pTree);
			continue;
		}
		else if(select == 1)
		{
			printf("\nPlease input the node of you wand to delete\n");
			scanf("%d",&nValue);
			DeleteRBTNode(pTree,&pTree,nValue);
			printf("\nAfter Delete the Node [%d],ther MidReverse:\n",nValue);
			MidOrderTree(pTree);
			continue;
		}

	}

	return 0;
}

代码测试（color后面：0表示红 1表示黑）

创建的红黑树如下：
代码结果：
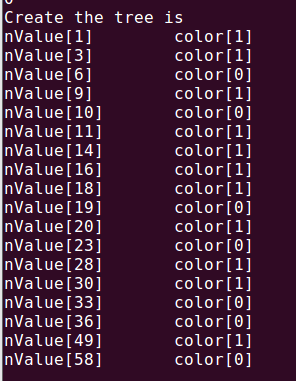上面的图是用红黑树网站插入创建的，下面是自己代码显示的结果，结果显示创建的红黑树和网站的结果相同

删除节点36：（情况）2.1
网站删除结果
自己代码删除结果

删除节点20：（情况）2.2.1

网站结果
代码结果

删除30：情况2.2.2.2.2.2
网站结果

代码结果

注意事项:

1 在删除结点时，如果删除的结点有孩子，那么在将爷爷指针指向孙子的同时，别忘了将孙子的父指针重新链接到新的父亲。
2 对每一种情况进行操作时，这种情况操作后可能会变成另一种情况，需要重新判断。
3 在重新判断之前记得要更新兄弟，父亲，侄子的结点信息（如果信息发生改变的话）
4 在两侄子全黑时，记得要先判断pNode是否是根，然后再进行重新判断，以免发生段错误
总结：这里的删除操作，每一次都是接着上一次的删除，就不全部试了，如果你们感兴趣可以自己测试一下。

如果你觉得这篇文章对你有帮助，欢迎评论，转发（著名出处）、点赞、关注哈，您的支持就是我创作的最大动力！文中如有错误，欢迎指正！！！