只出现一次的数字i
题目描述
题目分析
xxxx这道题第一次看的时候是完全没有思路的。想出来的方法效率太低。后来在网上看到解法是使用异或,但是一直不理解原理是什么。最近学校在学“计算机组成原理”,详细学异或后。突然对这个题有了透彻的理解。题目分析如下:
首先来了解一下异或这个操作符
异或(^):相同为0,相异为1
| 操作数1 | 操作数2 | 结果 |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
于是这种机理就可以很好的运用到解决这个问题当中。因为相同的数,在32个比特位的数分别相同,所以当相同的数字进行异或时,得到的结果将是32个比
特位全为0。得到的就是数字0。同时0与任何数字异或得到的仍然是该数字。
详细如图:
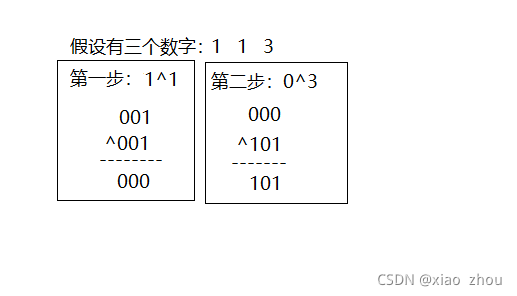
xxxx值得注意的是,最终异或的结果与数字的顺序无关。因为所有数字某一个比特位0、1数字个数一样的,异或起来值是一定的,与顺序无关。
代码实现:
class Solution {
public:
int singleNumber(vector<int>& nums) {
//最终的结果保存到变量a中
int a = 0;
for(size_t i = 0; i<nums.size(); i++)
//a与每一个数字异或
a ^= nums[i];
//a就是单独的那个数字
return a;
}
};
只出现一次的数字ii
题目描述
题目分析
xxxx不同上一个题,这个题目是只有一个数字出现一次,其余数字出现三次。显然无法使用上个题目的解法,但是大的思路还是对比特位进行操作。突破口就是想一下,这些数字的比特位有什么区别于联系。容易想到的是,对于每个数字的第i个比特位(1≤i≤32)来说,要么有些数字是1,要么是0。那么将每个数字同一比特位的1统计出来第,统计的结果要么是3的倍数,要么是3的倍数+1。而且,那些3的倍数+1的比特位,一定是只出现过一次的那个数字为1的比特位。
举一个例子:

xxxx在统计完所有数字每一位为1的个数后,我们就可以筛选出哪些比特位1的数字为3的倍数+1,这些位就是只出现一次数字的为1的比特位。然后我们就可以得到
这个唯一的数值了。
代码实现
class Solution {
public:
int singleNumber(vector<int>& nums) {
//cout数组用来存放统计32个比特位分别有多少个1
int count[32] = {0};
for(int i=0;i<nums.size();i++)
{
for(int j=0;j<32;j++)
{
//nums[i]&1得到该为是1还是0
count[j] += (nums[i]&1);
//>>用于一次获取一个数字的每一位
nums[i] = nums[i]>>1;
}
}
int number = 0;
for(int i=0;i<32;i++)
{
//如果是3的倍数+1
if(count[i]%3 == 1)
{
// number |= (1<<i)比较难理解,在下面展开具体说明
number |= (1<<i);
}
}
return number;
}
};
"number |= (1<<i)" 的详细解读:i从0~31,因此1<< i就是以此产生不同的二进制中只有一个1其余全为0的数字。这样就可以与结果数字的比特位中应该1的位置依次或运算。最终得到结果。
如图:

只出现一次的数字iii
题目描述
题目分析
xxxx看到这个题是不是感觉很熟悉,很亲切。似乎好像感觉跟上面的第一题十分相似。但是为啥一个是简单分类,一个是中等难度分类。顿时心中一凉。就像上学时候,这题看的这么眼熟,就是不会做。我也是在这道题卡了很久。感觉需要用到第一题的思路,但是这里有两个只出现一次的数字,生搬硬套肯定是不行的。想要转移的第一道题,关键就是把这两个只出现一次的数字分开,然后我们就可以对分开的两组数字,分别套用第一题的思路,就找出来了两个只出现一次的数字所以,关键就在于,如何将这一组数据分成两组,并且保证这两个出现一次的数字还分别在两个组。
xxxx毫无疑问,我们还是需要利用他们的二进制来找突破口。想要将他们分成两组,那么就需要找出他们的不同之处。那就是,对于不同的数字,他们的32个比特位不可能完全相同,所以必然有某几位不相同,我们就可以依据这个条件来把一组数据分成两组,该比特位为1的一组,为0的另一组。同时,其他成对出现的数字中,有可能该比特位为1或者为0.。不管他们具体如何,在分成两组之后,每一组都会退化成第一题的情况,那就是只有一个出现一次的数字,其余数字都是成对出现。再使用第一题的思路即可解决。
xxxx但是如何找出那个关键的比特位呢?我们可以将所有数字异或。通过之前的知识,我们知道,所有数字异或,成对出现的数字全部抵消,剩下的就是两个只出现过一次的数字,然后他们异或产生的数字,必然不可能是0,所以就会有其中一个比特位值为1,该比特位就是两个数字不同的比特位之一。
代码实现
class Solution {
public:
vector<int> singleNumber(vector<int>& nums) {
//val用于存储所有数字异或的结果
int val;
for(int j=0;j<nums.size();j++)
val ^= nums[j];
//i用来存储第几个比特位是1
int i = 0;
//找到val第几个比特位的值为1
//不是1,就进入循环,i++
while(!(1&(val>>i)))
{
i++;
}
//创建两个vector,存放分成的两组数据
vector<int> v1;
vector<int> v2;
//分组
for(int j=0;j<nums.size();j++)
{
//第i+1为是1的放入v1
if(nums[j]&(1<<i))
v1.push_back(nums[j]);
//第i+1为是0的放入v2
else
v2.push_back(nums[j]);
}
//套用第一题的思路
int a = 0,b = 0;
for(int j=0;j<v1.size();j++)
a ^= v1[j];
for(int j=0;j<v2.size();j++)
b ^= v2[j];
vector<int> ret;
ret.push_back(a);
ret.push_back(b);
return ret;
}
};
总结
这三道题的答题思路是相同的,都是使用了位运算。因为数字完全未知,我们要找数字之间的相同点与不同点,就需要依赖他们的二进制数。不同数字的二进制数一定不一样,相同数字的二进制数一定一样。
同时我们还需要掌握的就是。相同数字异或为0,0与任何数字异或为它本身。这个小技巧还用于不适用临时变量交换两个数字。
好啦,本文内容到此结束,如果思路和代码还有什么优化和改进的地方请在评论区发表,或者直接私信我。让我们共同学习共同进步!
