二叉树(Binary tree)
是树形结构的一个重要类型二叉树特点是每个结点最多只能有两棵子树,且有左右之分
二分搜索树(英语:Binary Search Tree),
也称为 二叉查找树 、二叉搜索树 、有序二叉树或排序二叉树。满足以下几个条件:
- 若它的左子树不为空,左子树上所有节点的值都小于它的根节点。
- 若它的右子树不为空,右子树上所有的节点的值都大于它的根节点
- 它的左、右子树也都是二分搜索树。
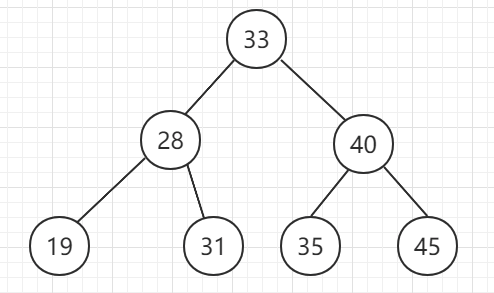
实现二分搜索树结构
public class BST<E extends Comparable<E>> {
private class Node {
public E e;
public Node left, right;
public Node(E e) {
this.e = e;
left = null;
right = null;
}
}
private Node root;
private int size;
public BST() {
root=null;
size=0;
}
public int size(){
return size;
}
public boolean isEmpty(){
return size == 0;
}
}
向二分搜索树中添加元素
package com.qcx.algo.day15.v1;
/**
* @ Author :Eric Lee
* @ Date :Created in 21:49 2021/9/5
* @ Description:
* @ Modified By:
* @ Version : 1.0
*/
public class BST<E extends Comparable<E>> {
private class Node {
public E e;
public Node left, right;
public Node(E e) {
this.e = e;
left = null;
right = null;
}
}
private Node root;
private int size;
public BST() {
root=null;
size=0;
}
public int size(){
return size;
}
public boolean isEmpty(){
return size == 0;
}
// 向二分搜索树中添加新的元素e
public void add(E e){
if (root == null){
root = new Node(e);
size++;
}else {
add(root, e);
}
}
// 向以node为根的二分搜索树中插入元素e,递归算法
public void add(Node node, E e){
// 暂时不支持相等元素的添加
if (e.equals(node.e))
return;
else if (e.compareTo(node.e) < 0 && node.left == null){
node.left = new Node(e);
size ++;
return;
}else if (e.compareTo(node.e) > 0 && node.right == null){
node.right = new Node(e);
size ++;
return;
}
// 向左子树中添加元素
if (e.compareTo(node.e) < 0)
add(node.left, e);
else if (e.compareTo(node.e) > 0)
add(node.right, e);
}
}
另一种add方式
public Node add(Node node, E e){
if (node == null){
size ++;
return new Node(e);
}
if (e.compareTo(node.e) < 0)
node.left = add(node.left, e);
else if (e.compareTo(node.e) > 0)
node.right = add(node.right, e);
return node;
}
非递归的添加
// 非递归实现添加
public void add2(Node node, E e){
if (node == null){
root = new Node(e);
size ++;
return;
}
Node p = root;
while (p != null){
if (e.compareTo(p.e) < 0){
if (p.left == null){
p.left = new Node(e);
size ++;
return;
}
p = p.left;
}else if (e.compareTo(p.e) > 0){
if (p.right == null){
p.right = new Node(e);
size ++;
return;
}
p = p.right;
}
else return;
}
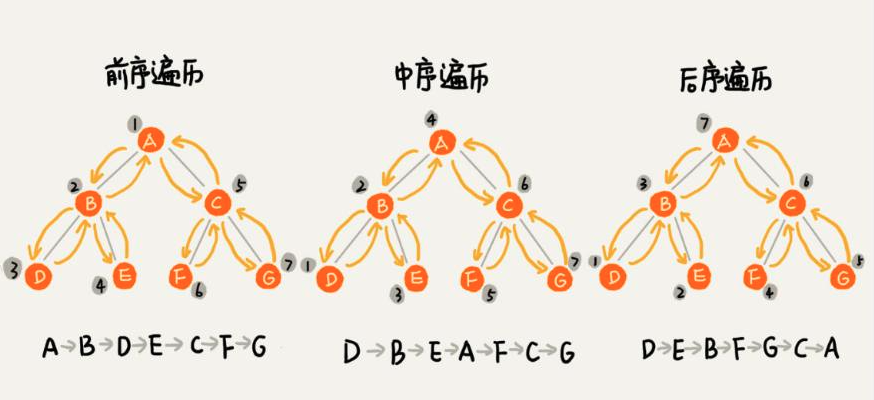
D、L、R 分别代表遍历根结点、遍历左子树、遍历右子树
-
DLR–前序遍历(根在前,从左往右,一棵树的根永远在左子树前面,左子树又永远在右子树前面 )
-
LDR–中序遍历(根在中,从左往右,一棵树的左子树永远在根前面,根永远在右子树前面)
-
LRD–后序遍历(根在后,从左往右,一棵树的左子树永远在右子树前面,右子树永远在根前面)
package com.qcx.algo.day15.v1;
/**
* @ Author :Eric Lee
* @ Date :Created in 21:49 2021/9/5
* @ Description:
* @ Modified By:
* @ Version : 1.0
*/
public class BST<E extends Comparable<E>> {
private class Node {
public E e;
public Node left, right;
public Node(E e) {
this.e = e;
left = null;
right = null;
}
}
private Node root;
private int size;
public BST() {
root = null;
size = 0;
}
public int size() {
return size;
}
public boolean isEmpty() {
return size == 0;
}
// 向二分搜索树中添加新的元素e
public void add(E e) {
if (root == null) {
root = new Node(e);
size++;
} else {
add(root, e);
}
}
// 向以node为根的二分搜索树中插入元素e,递归算法
// public void add(Node node, E e){
// // 暂时不支持相等元素的添加
// if (e.equals(node.e))
// return;
// else if (e.compareTo(node.e) < 0 && node.left == null){
// node.left = new Node(e);
// size ++;
// return;
// }else if (e.compareTo(node.e) > 0 && node.right == null){
// node.right = new Node(e);
// size ++;
// return;
// }
// // 向左子树中添加元素
// if (e.compareTo(node.e) < 0)
// add(node.left, e);
// else if (e.compareTo(node.e) > 0)
// add(node.right, e);
//
// }
// 向以node为根的二分搜索树中插入元素e,递归算法
public Node add(Node node, E e) {
if (node == null) {
size++;
return new Node(e);
}
if (e.compareTo(node.e) < 0) node.left = add(node.left, e);
else if (e.compareTo(node.e) > 0) node.right = add(node.right, e);
return node;
}
// 非递归实现添加
public void add2(Node node, E e) {
if (node == null) {
root = new Node(e);
size++;
return;
}
Node p = root;
while (p != null) {
if (e.compareTo(p.e) < 0) {
if (p.left == null) {
p.left = new Node(e);
size++;
return;
}
p = p.left;
} else if (e.compareTo(p.e) > 0) {
if (p.right == null) {
p.right = new Node(e);
size++;
return;
}
p = p.right;
} else return;
}
}
// 看二分搜索树中是否包含元素e
public boolean contains(E e) {
return contains(root, e);
}
public boolean contains(Node node, E e) {
if (node == null)
return false;
if (e.compareTo(node.e) == 0)
return true;
else if(e.compareTo(node.e) < 0)
return contains(node.left, e);
else
return contains(node.right, e);
}
// 二分搜索树的前序遍历
public void preOrder(){
preOrder(root);
}
public void preOrder(Node node){
if (node == null)
return;
System.out.println(node.e);
preOrder(node.left);
preOrder(node.right);
}
}
测试
package com.qcx.algo.day15.v1;
import org.omg.CORBA.INTERNAL;
/**
* @ Author :Eric Lee
* @ Date :Created in 22:52 2021/9/5
* @ Description:
* @ Modified By:
* @ Version : 1.0
*/
public class Main {
public static void main(String[] args) {
BST<Integer> bst = new BST<>();
Integer[] nums = {5, 3, 6, 8, 4, 2};
for (int num : nums)
bst.add(num);
/
// 5 //
// / \ //
// 3 6 //
// / \ \ //
// 2 4 8 //
/
bst.preOrder();
System.out.println(bst.contains(8));
System.out.println(bst.contains(10));
}
}
中序遍历
// 二分搜索树的中序遍历
public void inOrder(){
inOrder(root);
}
// 中序遍历以node为根的二分搜索树, 递归算法
public void inOrder(Node node){
if (node == null)
return;
inOrder(node.left);
System.out.println(node.e);
inOrder(node.right);
}
// 二分搜索树的后序遍历
后序遍历
public void postOrder(){
postOrder(root);
}
public void postOrder(Node node){
if (node == null)
return;
postOrder(node.left);
postOrder(node.right);
System.out.println(node.e);
}