前言
堆的性质:堆中某个节点的值总是不大于或不小于其父节点的值;堆总是一棵完全二叉树。
注意区分,二叉树的堆是一种数据结构,而系统层的堆是操作系统中管理内存的一块区域分段,不要弄混淆了。
一、预备小知识
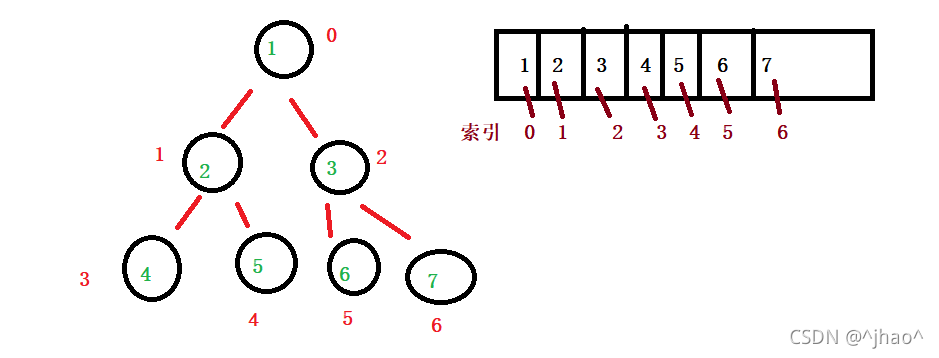
观察上图我们能够得到以下几个结论:
第一个:顺序表作为堆的储存结构的是比较合适的,因为这样子我们用的顺序表就可以不会存在空间的浪费,比如前面出现NULL之类的,所以我们用顺序表作为堆的储存结构,它的逻辑结构是一颗满二叉树,并且作为堆还要满足每个父亲大于孩子或者每个父亲都小于孩子
第二个:每个节点它的左孩子若是存在,左孩子的下标就一定是(父亲的下标*2+1),而每个孩子它的父亲则是(父亲的下标 =(孩子的下标-1)/2),也就是我们这里的结论能够找到当前节点的孩子节点和父亲节点。
二、建堆
1.初始化堆(小堆为例)
假设给定一个数组,我们去初始化堆,这里是有两种方法
给定数组:int array[] = {27,15,19,18,28,34,65,49,25,37};
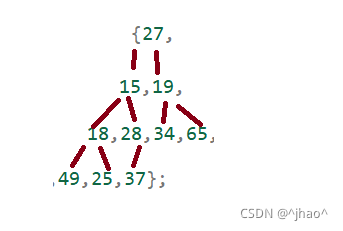
方法一:倘若我们的堆已经像上图一样,根的左子树和右子树都已经是一个小堆了,我们如何通过算法来使他变成一个小堆
向下调整算法:当一个节点的左右子树都是堆的时候适用
观察我们要调整27的话,我们27的每一次变动都会影响到左右子树,所以我们要保证不影响左右子树的堆性质的同时改变它的储存结构。方法也就是将它的左孩子和右孩子当中挑选小的,和根进行交换,这时对于其中的一边子树,如图中的19一路,当15与27交换的时候,实际上不改变19这个子树的堆的性质,但是对于15的子树我们换了一个更大的数,而我们建的是小堆,所以对于15的这颗子树,我们也要像处理27的逻辑一样,直到出现交换到了根节点或者父节点比左右孩子都小。
//向下调整算法,a为底层结构的数组,n为调整的数组的大小,parent为调整的节点
void AdjustDown(int* a,int n ,int parent)
{
//适合左右都是堆,parent不满足的情况的排序
//每一个parent都有可能要交换到叶子
int child = parent * 2 + 1;
//排序的节点一定会有左孩子
while (child<n)
{
//小堆为例
if (child + 1 < n && a[child] > a[child + 1])
child++;
if (a[child] < a[parent])
Swap(&a[child], &a[parent]);
else//表示父亲比最小孩子的孩子小,满足堆
break;
//走到这里,表示进行了交换,还要继续往下走
parent = child;
child = parent * 2 + 1;
}
}
走到这里,我们仅仅只是处理了当左右子树都是小根堆的情况,那如果不满足的时候我们该怎么解决呢,如下图:
这个时候其实我们可以看到从索引为2的地方(即最后一个父节点,索引为最顺序表中最后一个数的下标(n - 1 - 1) / 2)其中n 为数组的大小,它的左子树和右子树都只有一个数,那么也是可以认为是一个左右子树都已经是堆的结构,我们就可以从索引为2倒着更新 2 --> 1 --> 0,当我们走到0的时候,0的左右子树就都是小根堆了,这样子我们就可以用向下调整算法弄出一个小根堆
代码如下:
void HeapSort(int* a, int n)
{
//我们从最后一个父节点开始建堆,从后向前遍历
//这样就能保证都是小堆
//对节点用向下调整就可以了,这里我们建小堆
//这里的 n-1是最后一个数的索引, (n-1-1)/2是他的父亲索引!
for (int i = (n - 1 - 1) / 2; i >= 0; --i)
{
//i表示我们传参的父节点
AdjustDown(a, n, i);
}
}
走到这里第一种初始化堆的方式说完啦!!!
int arr[] ={20,30,60,25,27,55,57};
接着第二种:向下调整算法可以做到初始化堆,向上调整算法其实也是可以的,其实这里与之后讲的根的插入的思想类似,也就是当我们数组只有20的时候我们通过插入30来保证是一个小堆,然后插入60保证是一个小堆(图一:可以发现都不用调整)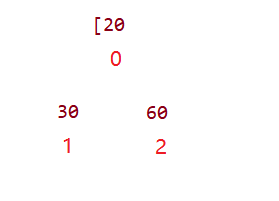
我们再继续插入25又会如何呢(下图),可以发现当我们插入时不满足30是一个小堆,所以我们将30 与 25 交换,这样原来的1号索引的树就是一个小堆了,但对于1号索引的父亲,我们将一个比1号索引小的数(25)放到1号位置,我们这个时候其实还是要进行1号位和他的父亲(0号位),倘若0号位比1号位小,则结束,不然就交换,迭代到根,也结束!! 所以向上调整算法的思想也比较简单,也就是迭代到满足条件即可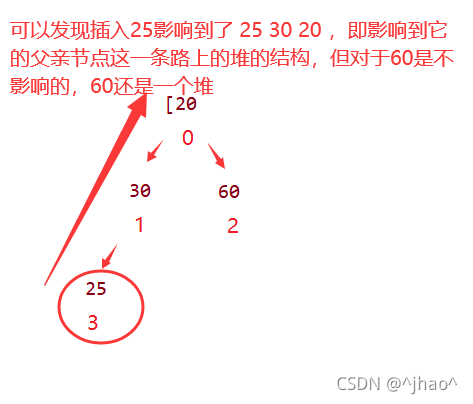
向上调整的代码:
void AdjustUp(HPDataType* a, int child)
{
assert(a);
int parent = (child - 1) / 2;
while (child > 0)
{
if (a[child] < a[parent])
{
Swap(&a[child], &a[parent]);
//再进行迭代
child = parent;
//注意parent在这里不可能会是负数
parent = (parent - 1) / 2;
}
else
{
break;
}
}
}
2.证明建堆的复杂度
当我们是用向下调整算法来建堆的话吧
画的有点丑,但是意思就是从最后一个父节点更新节点*它的更新层数

三、堆的插入
堆的插入其实可以先将数据放在顺序表的尾,然后再通过一次向上调整算法就可以实现一次堆的插入,如原数据{1,2,3}后面插入0
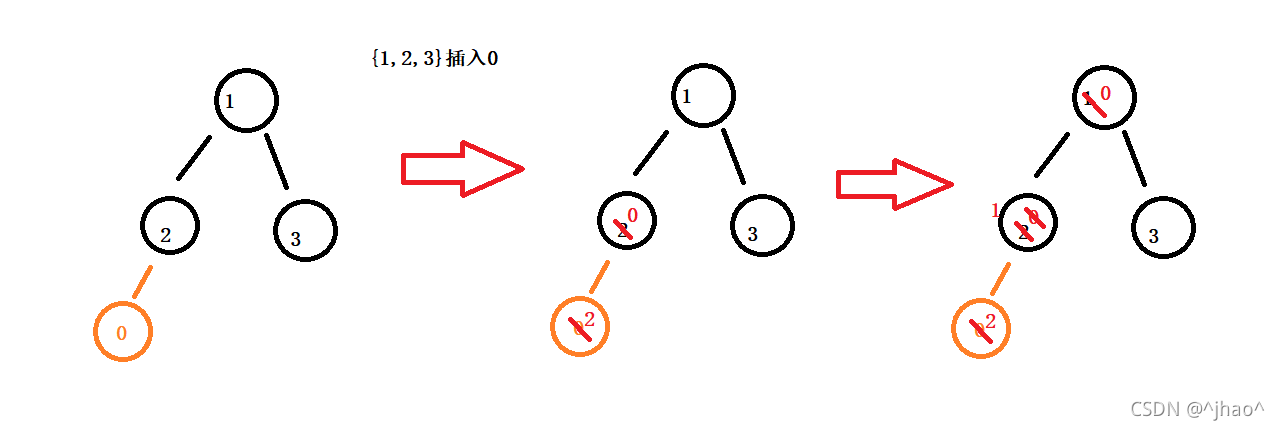
代码:
void HeapPush(Heap* hp, HPDataType x)
{
//插入一个数在数组的末尾,在用向上调整算法(只影响一条路径)
//注意考虑增容
assert(hp);
if (hp->_capacity == hp->_size)
{
int newcpacity = hp->_capacity * 2;
HPDataType*tmp = realloc(hp->_a, newcpacity * sizeof(HPDataType));
if (tmp == NULL)
{
printf("realloc fail\n");
exit(-1);
}
hp->_a = tmp;
hp->_capacity = newcpacity;
}
//走到这里,空间都是足够的
hp->_a[hp->_size++] = x;
AdjustUp(hp->_a, hp->_size-1);
}
插入数据前需要检测容量,然后放在数组尾,++size,再用向上调整算法即可。
四、堆的删除
堆的删除一般是删除头的数据,因为这样子能够少的破坏左右子树堆的结构。
不然的话删除数据之后又需要重新建堆O(N),这样子的删除效率效率太低了,我们可以将头和尾的数据进行交换,size–之后再对头进行向下调整算法,这时候刚好因为没破坏左右子树是堆所以可以使用
void HeapPop(Heap* hp)
{
//删除一个数据可以让第一个数据和最后一个数据交换
//hp的size--之后就可以对第一个数进行向下调整算法
assert(hp);
assert(!HeapEmpty(hp));
Swap(&hp->_a[--hp->_size], &hp->_a[0]);
AdjustDown(hp->_a, hp->_size, 0);
}
五、TopK问题
现在我们需要从(N)10亿个整数当中挑选最大的(K)10个,怎么做?
首先解释一下为什么挑选最大的10个数要建小堆,如果建大堆,最大的数可能挡在头的位置,其他9个次大的数就进不来。所以建小堆就可以将最大的数更新进堆中!
1.首先这里有4g的字节,如果需要排序的话放到内存当中排可能会因为内存不够排放不了,加入能排那我们的时间复杂度也是O(NlogN),
2.其次我们可以考虑建堆,如果正常思路建堆:即建一个10亿个数的小堆,实际内存也存不下,假设存的下的话,建堆的时间复杂度是O(N),K个数选出来是O(KlogN),总共时间复杂度O(N+KlogN)–>10亿加300,效率比起排序还是会好一些的。那么还有没有更好的方法呢?
3. 还是建堆,我们建一个10个数的小堆,将(10亿-10)个数依次放入堆中,建堆的时间复杂度O(K),找到K个数的时间复杂度(NlogK),时间复杂度就是O(K+NlogK)–>10+40亿,但是空间只开了O(K)个,当K小的时候,是十分优秀的了!
结论:乍一看,第二种的时间复杂度可能还会好一些,实际上和第三种都是在一个量级的,实际上当我们N为100亿的时候都已经不可能建堆了,因为它的空间复杂度为O(N),而我们的第三种方法的空间复杂度为O(K),所以在时间复杂度差不多的情况下,对于空间消耗的topK的解法实际上更受到我们欢迎!
void PrintTopK(int* a, int n, int k)
{
//假设从N个数当中挑选最大的K个
//拿前k个数初始化,当我们要挑选最大的前K个数的时候
//我们选择建小堆,这样才不会被最大的数挡在a[0]这个位置
//先对开始的数组进行建堆
for (int i = (k - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(a, k, i);
}
for (int i = k; i < n; ++i)
{
//遍历下标【k ,n-1】的数,依次在我们的堆里面比较
//当有一个数比我们的堆顶大的时候我们就覆盖就可以
if (a[0] < a[i])
{
a[0] = a[i];
AdjustDown(a, k, 0);
}
}
}
void TestTopk()
{
int* a=(int*)malloc(sizeof(int)*100000);
srand(0);
//创建100000(N)随机数并且都小于10000
for (int i = 0; i < 100000; i++)
{
a[i] = rand()%10000;
}
//创建随机十个位置(K)大于10000,观察程序能否找到
a[1024] = 10001;
a[10240] = 10002;
a[10204] = 10003;
a[10024] = 10005;
a[10125] = 100000;
a[10224] = 10004;
a[10234] = 1000100;
a[10214] = 10006;
a[15044] = 10009000;
a[15045] = 10009001;
PrintTopK(a, 100000, 10);
for (int i = 0; i < 10; i++)
{
printf("%d ", a[i]);
}
printf("\n");
}

实际上在我们后面学习c++的时候接触到仿函数的时候,我们可以通过传参的方式来确认我们建的是大堆还是小堆,priority_queue的底层就是一个堆,当然他可以用我们这里的顺序表vector,也可用deque双端队列来实现。
全部代码
总结
堆的就到此结束啦,之后在C++的优先级队列当中会用到这里的知识,到时候的实现实际上也是差不多的,有帮助的一键三连吧!!!