[数据结构与算法]某区间内相邻两位之差至少为2的数的个数（数位dp）

题目：https://www.acwing.com/problem/content/1085/
题意：Windy 定义了一种 Windy 数：不含前导零且相邻两个数字之差至少为 2 的正整数被称为 Windy 数。Windy 想知道，在 A 和 B 之间，包括 A 和 B，总共有多少个 Windy 数？ 1≤A≤B≤2×10^9
样例：[1 10]–9 [25 50]–20

题解：数位dp。
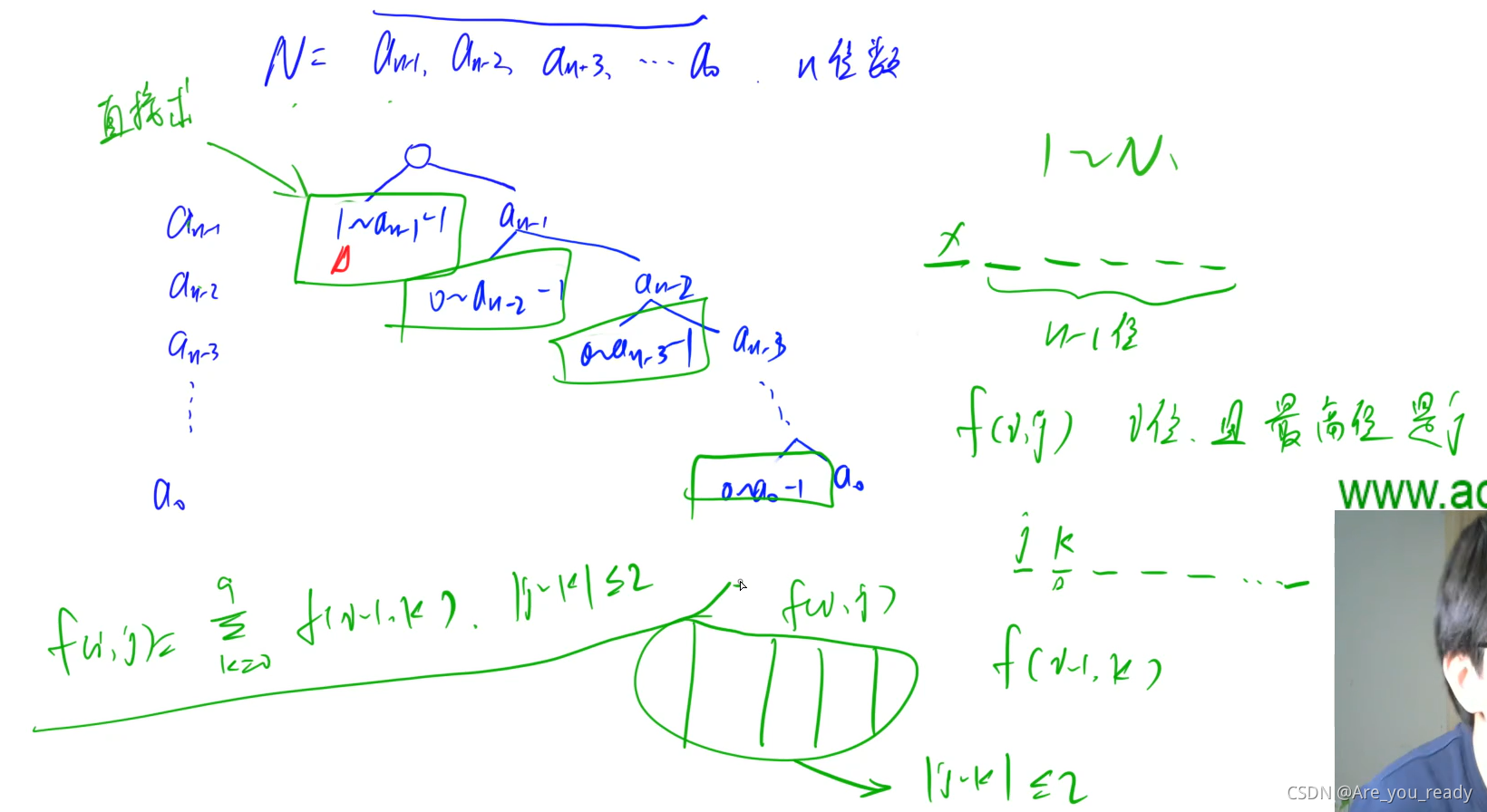
首先：数位dp老套路，要求[l,r]内符合题目限制的数的个数，那么只需要求出[0,r]的个数和 [0,l-1]的个数，两个相互一减，就是[l,r]的个数。
其次：先做个dp预处理，f[i][j]表示总共有i位，最高位为j的情况下可行的方案数。有了这个预处理后，从最高位开始枚举每一位可以挑选的数，假如某位为x，那么从[0,x-1]枚举一下能够和x之差大于等于2的数，叠加上这种位数情况下最高位为枚举的那个数的所有方案数即可。
但是有一个特别需要注意的点，最高位枚举[1,x-1]即可，不能从0开始枚举，不然会出问题，如果从0开始枚举，就会在最高位叠加一个f[i][0]，这里会有问题。
比如说，俩位的时候，枚举最高位为0，那么答案就是09-08-07-06-05-04-03-02,答案是8，但是答案是9，因为1也可以作为答案，例如样例[1,10]答案就是9，所以答案是不对的，这里两位的时候对答案的影响是1，更多位的时候，如果枚举最高位为0，那么答案会差更多，毕竟在dp中，一个状态对应很多数。但是对于如果最高为是>=1的数，它的其它位是可以枚举0的，没有任何影响。
最高位为0的解决方案，其实很容易解决，比如如果n是8位的话，在下面直接暴力跑位数为1、2、3、4、5、6、7的情况就行了，因为8位的情况在数位dp中已经跑完了(因为最高位没有枚举0的情况),最高位为0的情况，就是剩下的这些位数的所有情况，而这些所有情况一定都小于n，所有都符合，直接暴力跑一下这些位的所有情况，叠加f[i][j]就可以了。

#include <bits/stdc++.h>
//#define int long long
#define pb push_back
#define pii pair<int, int>
#define mpr make_pair
#define ms(a, b) memset((a), (b), sizeof(a))
#define x first
#define y second
typedef long long ll;
typedef unsigned long long LL;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
using namespace std;

const int N = 15;
int f[N][N];  // f[i,j]总共有i位，最高位是j的方案数
void init() {
    //首先枚举1位的情况
    for (int i = 0; i <= 9; i++) f[1][i] = 1;
    // dp跑出总共有i位，最高位是j的方案数
    for (int i = 2; i < N; i++)
        for (int j = 0; j <= 9; j++)
            for (int k = 0; k <= 9; k++)
                if (abs(j - k) >= 2) f[i][j] += f[i - 1][k];
    // printf("%d %d\n", f[1][0], f[2][0]);
}

int dp(int n) {
    if (!n) return 0;
    vector<int> nums;
    while (n) nums.emplace_back(n % 10), n /= 10;
    int res = 0;
    int last = -2;  //初始保证0-9不会受到last影响
    //从最高位开始枚举每一位
    for (int i = nums.size() - 1; i >= 0; i--) {
        int x = nums[i];
        //如果是最高位的话，从1开始枚举，0的情况比较特殊，在下面单独跑出结果
        for (int j = i == nums.size() - 1; j < x; j++) {
            if (abs(j - last) >= 2) res += f[i + 1][j];
        }
        //如够这一位和上一位之差小于2，那么就没必要跑了
        if (abs(x - last) >= 2)
            last = x;
        else
            break;
        //如果还没有跳出，那么本身也是
        if (!i) res++;
    }
    //暴力跑位数小n的所有情况，因为这些情况都比n小，只要符合限制条件，就是可行方案
    //而和n位数相同的数，已经在上面的数位dp中跑完了
    for (int i = 1; i < nums.size(); i++)
        for (int j = 1; j <= 9; j++) res += f[i][j];
    return res;
}
signed main() {
    init();
    int l, r;
    cin >> l >> r;
    printf("%d\n", dp(r) - dp(l - 1));
    return 0;
}