[数据结构与算法]Cell Decomposition系列路径规划算法——PCD

Cell Decomposition系列路径规划算法——PCD

做个正直的人

思想

PCD是目前Cell Decomposition算法中，我认为表现最好的。
基于概率的算法（比如RRT、PCD）和确定性算法（比如A*、Dijkstra）相比，不需要显式的表达，因而在高维问题中具有相当大的优势。可以大大节省计算量和空间需求。

• PCD虽然是基于ACD的，也是对各个cell进行不同粒度的分解，也是采用固定的形状，但是PCD中的cell是free还是occupied并不是确定的，而是概率的。PCD在一个cell中进行采样，如果所有的采样都是free，那么，这一个cell就被认为是 possibly free cell；如果所有的采样都是occupied，那么，这一个cell就被认为是possibly occupied cell；如果采样中，有free，有occupied，那么这一个cell被认为是known to be mixed，也就是需要被分解成前两个类型。
• 在一轮分解完成之后，采用一个图搜索算法去搜索一个连接init和goal的cell队列，称为通道channel。
• 搜索到一个通道之后，就会检查相应的path是不是安全，不安全就分解那一个不安全的possibly free cell；若是没有搜索到这样一个通道，那么说明当前的所有possibly free cell还没有连接成1个连通图，这肯定是因为有possibly occupied cell把这两个子连通图给隔开了，那么PCD就去这些possibly occupied cell采样并分解。

这一些步骤迭代下去，就能找到一个连接init和goal的path。下面具体的讲解一下PCD算法的细节。

1、表示

我们把一个cell $k_i$划分为以下三类之一

• possibly free cell，if 该cell内的采样都是free
• possibly occupied cell，if 该cell内的采样都是occupied
• known to be mixed，if 该cell内的采样有free，有occupied

包含了起始位置$q_{init}$和$q_{goal}$的cell分别记为$K_{init}$和$K_{goal}$。

在图搜索阶段，我们把每一个possibly free cell都看作是一个node，如果两个possibly free cell是相邻的（有公共边），那么我们就把这两个cell对应的node用edge给连接起来。最后我们就可以得到一些个连通图。

包含了$K_{init}$的连通图记为开始区域$R_{init}$。

包含了$K_{goal}$的连通图记为目标区域$R_{goal}$。

搜索阶段我们找到的那一系列连接$K_{init}$和$K_{goal}$的cells称为一个通道channel。

2、算法步骤

1. 初始化：把整个地图看做一个cell，这个cell中有两个采样点$q_{init}$和$q_{goal}$，很明显这个最初的cell是possibly free cell。并且$K_{init}=K_{goal}=C_{work}$。
2. 搜索阶段：返回一个连接了$K_{init}$和$K_{goal}$的channel，在最开始也就是我们最初的这一个大cell。但是我们也有可能面临找不到channel的情况。这种时候转5。
3. 检查阶段：反回了一个channel，且$q_{init}$和$q_{goal}$在同一个cell内部，由于cell是凸的，所以我们可以把$q_{init}$和$q_{goal}$用一段直线段连起来，并且检查这一个path是不是安全。如果安全，算法结束；如果不安全，转4。（不用说，大概率上都是不安全的）
4. 转到这里，说明你在检查阶段碰到了不安全的路径。我们把检查出来不安全的那一个possibly free cell修改为known to be mixed，并且对其进行分解。分解完成后转2。
5. 转到这里说明你在搜索阶段没有找到channel。想一想为什么。如果$K_{init}$和$K_{goal}$在同一个连通图上，那怎么可能找不到channel呢？所以很明显，$K_{init}$和$K_{goal}$此时位于两个不同的图中，他们之间不是连通的。也就是有一些possibly occupied cell把$K_{init}$和$K_{goal}$所属的两个连通图给隔离开了。因此我们现在的任务就是去那些possibly occupied cell中去采样，并把它们分解。分解完成后转2。

3、算法细节

3.1 cell形状

PCD把cell形状选为rectangloid，也就是正交的，二维空间就是长方形，三维空间就是长方体，高位空间就是***（爱叫啥就叫啥吧）；总之，这些图形中的任意两邻边必定互相垂直。那么为什么这么选呢？

• 还能怎么选，高维空间呀，三维空间的几何就够难了，更高维空间肯定不是三维空间的生物能想明白的，几何形状肯定越简单越好啊。那么什么形状最简单？答：各边互相垂直的形状最简单。
• 这样的图行必定是凸的。为什么要求是凸的呀，因为在这样的图形中，任意两点的连线仍然位于图形内部。

但是，这样也有一些缺点，那就是有限数量的cell，没办法精确表示搜索空间。这很好理解吧。不说了。

3.2 图搜索

所有的possibly free cell 由node来表示，并组成一个图。每两个相邻的cell之间用一个edge来表示。edge的cost的确定可以选择不同的策略。PCD的作者用A*算法实现了图搜索。

3.3 局部路径规划LPP

一旦在搜索阶段找到了一条连接起点和终点的channel ψ = { K i n i t = K P 0 , K P 1 , . . . , K P n = K g o a l } ψ=\{K_{init}=K_{P_0},K_{P_1},...,K_{P_n}=K_{goal}\} ψ={Kinit?=KP0??,KP1??,...,KPn??=Kgoal?}
LPP必须根据这一个channel规划一个相应的、经过possibly free cell的path出来。

其实想一想，即便是经过possibly free cell的path也不能保证是安全的吧。但是我们再想一想，经过possibly free cell的path和经过possibly occupied cell的path都不能保证是安全的，但是毕竟还是有差距的，经过possibly free cell的path安全的概率还是要大一些的吧。

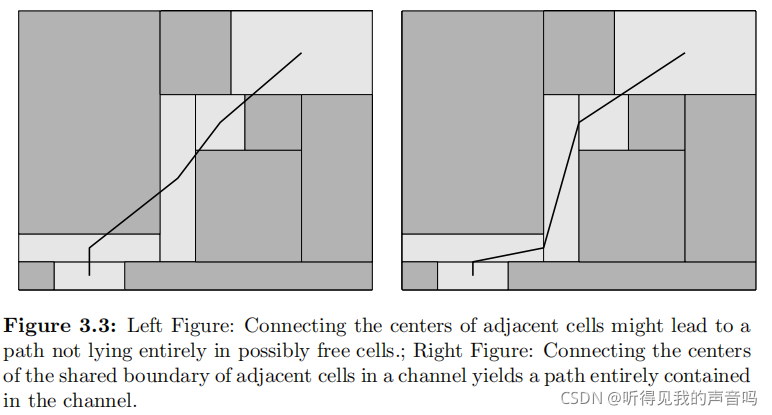
LPP有两种思路。一种是把channel中的cell的中心直接连起来，如下左图，这时候的path很可能要穿过possibly occupied cell。但是我们可以这么来想。

你这所有的cell不都是凸的吗？那么你这cell内部和边上的任意两点的连线都肯定位于这个cell内部。我们这么来看，channel中$K_{i?1}$和$K_i$是有一个公共边的（三维就是面，高维就是超平面），我们记为$S_{i?1}$；$K_i$和$K_{i+1}$也是有一个公共边的，我们记为$S_i$。很明显$S_{i?1}$和$S_i$各自中心的连线一定位于possibly free cell $K_i$内部，因而这一条path就全部位于possibly free cell内了。如下右图所示。

3.4 cell分解

一旦在possibly free cell中发现了碰撞点，或者在possibly occupied cell中发现了安全点，这一个cell就会被更改为known to be mixed，并且会被分解成possibly free cell和possibly occupied cell。我们尽量把碰撞点放在一个cell中，一般说来是分解成一个possibly occupied cell和$min(2n,m)$个possibly free cell。

那么我们怎么分解呢？要知道cell都是rectangloid的，所以我们必须沿着各个坐标轴进行分解。所以我们的策略就是

1. 找到相距最近的安全点比如$(0,0,0)$和碰撞点比如$(1,2,4)$
2. 找到这两个点各个维度中相距最远的那一个维度，比如第三维$x_3$
3. 将这两个采样点分别向该维度进行投影，并在两个投影点的中点处用一个垂直于该维度的超平面$x_3=2$分开。

3.5 概率采样

如果在图搜索阶段，我们没有找到任何一条channel，那么，我们需要对possibly occupied cell进行采样以扩展自由区域，进而方便我们找到一条channel。

3.6 算法结果

算法结果，详见下图

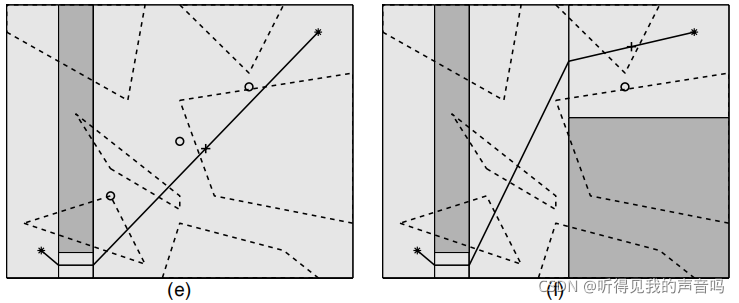
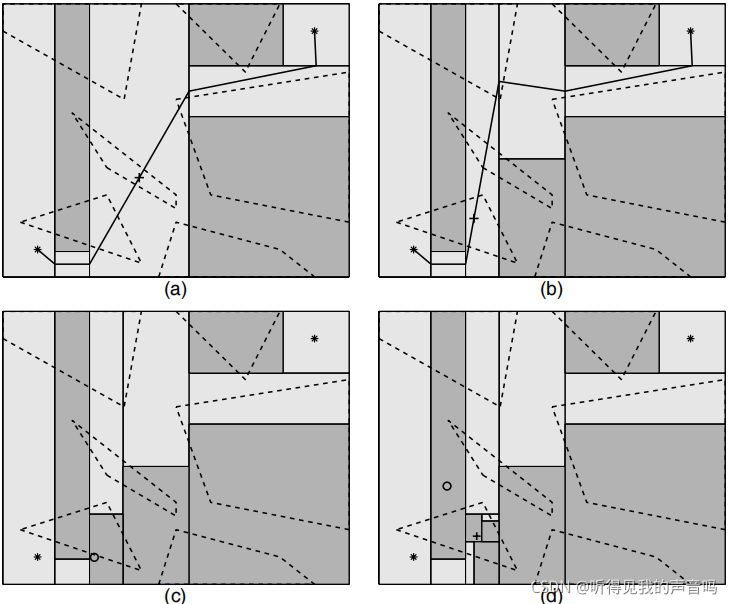
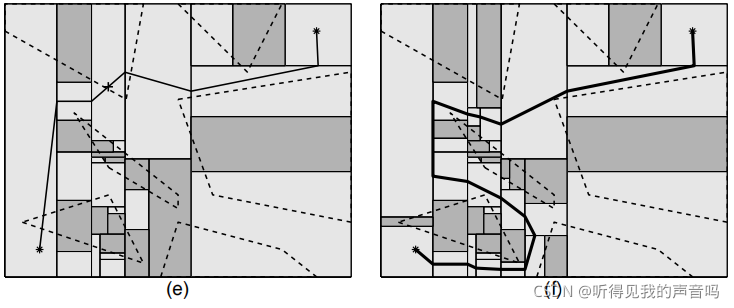
4、改进

4.1 概率采样

图搜索阶段，我们没有找到任何一个channel。这个时候我们不是说要采样possibly occupied cell吗？但是我们面临着两大问题：

1. 一个很大的possibly occupied cell可能把一个狭窄的通道给堵住了（其实就是狭窄通道位于这个大cell内部）。如果我们每次只采样一个点，那我们能够找到这一个狭窄通道的概率就很低。相应的，我们就需要重复多次才能够找到这一个狭窄通道，这样算法的效率就很低。
2. 我们真的需要对所有的possibly occupied cell都采样吗？让我们来思考一下，为什么我们没有找到一个可行的channel呢？是因为这个时候$K_{init}$和$K_{goal}$位于两个不连通的子图当中，我们当然找不到channel。那是什么原因让这两个子图不连通了呢？很明显，是因为有一些possibly occupied cell卡在了两个子图之间对不对。所以我们要做的是对这些cell进行采样，而不是对所有的cell都采样。

针对第二个问题，改进后的PCD不对所有的possibly occupied cell采样，而是只对那些感兴趣的cell（Interesting Possibly Occupied Cell，IPOC）进行采样。那么什么是IPOC呢？

还记得在一开始我们定义的开始区域$R_{init}$和目标区域$R_{goal}$吗？对所有的possibly occupied cell，我们把它们分层三类。

• 只和$R_{init}$相邻的possibly occupied cell
• 只和$R_{goal}$相邻的possibly occupied cell
• 同时和$R_{init}$与$R_{goal}$都相邻的possibly occupied cell。

那么导致我们搜索不到channel的是哪一类呢？很明显是第三类。看下图

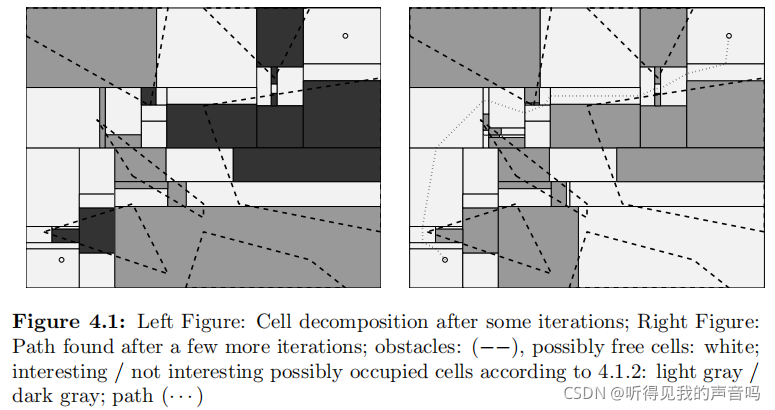
上图中，有三个颜色：白色、灰色、黑色。白色代表possibly free cell，灰色代表同时和$R_{init}$与$R_{goal}$都相邻的possibly occupied cell。黑色代表只和$R_{init}$或者$R_{goal}$两者之一相邻的possibly occupied cell。很明显，我们应该对灰色的possibly occupied cell进行采样。左图是采样并分解之前的，右图是采样并分解之后的。

4.2 图搜索策略

4.2.1 restart 还是 lazy

在搜索阶段，我们的目标是找到一条连接$K_{init}$和$K_{goal}$的channel。那么我们用什么搜索策略呢？

对于图搜索来说，A*貌似是一个比较不错的方法，但是我们来想一下，假如在图搜索阶段我们没有找到channel，我们是不是要去采样IPOC并分解然后重新搜索呀，那么，我们前一次的搜索结果有没有用，是该丢弃然后重新搜索，还是说上一次的搜索结果可以接着用呢？

很明显，我们仅仅是对那些IPOC进行了采样和分解，那原先的那些possibly free cell变了吗？没有变。那原先的那一部分图结构变了吗？也没有变，仅仅是在原先的图基础上增加了一些新的节点，并且原先的那些节点到起点的最短距离也没变，所以上一轮的搜索结果仍然是可用的。那么这种时候，我们无需进行重新的搜索（restart A*），而是可以直接在上一次搜索的基础上，继续搜索，这称为Lazy A*。

再来想一下，我们找到了一个channel。但是我们在检查阶段发现这一个path是不安全的，因而我们对那一个不安全的possibly free cell进行了分解。所以，这一个cell对应的那个node被删除了，又出现了一些新的node。可以想见，这一个node，被删除之后，是不是意味着图的结构发生了改变。那跟这个node有关联的其他node到起点的最短距离是不是也会随之改变。如果我们还想用上一次的搜索结果，那我们就必须把由于这一个node被删除和新node加入所引起的影响向后传播。

很容易理解，这一个node离起点越近，他的影响就越大，要传播的工作量也就越大。那我们就想一下，传播是需要代价的，重新搜索也是需要代价的，这两个代价哪一个更大呀？我们是不是得好好考虑一下。我们可以这么干，我设置一个阈值$T_{thred}$，如果传播的代价小于$T_{thred}$，那我们就传播。如果传播的代价大于$T_{thred}$，那我们就重新搜索（restart A**）。

4.2.2 optimal 还是 faster

解决了重新搜索还是lazy的问题，我们面临的另一个问题是：既然有检查阶段，就说明你在图搜索阶段找到的路径不能保证是安全的，那我在图搜索阶段还有必要非得找最优的那一个channel吗？毕竟连你可行不可行都不知道，我干嘛非要找最优的。我可不可以找一个次优的，但是我找的速度更快，可以吗？

这一个问题其实很好理解。但是对于解决办法，不同的人可能有不同的看法。就是在这里提出一种思路。

这是一种在工程领域中很常见的思想，称为——trade off。你可以翻译成平衡、取舍、交换、权衡。总之就是牺牲一些东西来换取一些东西。

5、PCD的问题

对狭窄通道表现不佳！

这似乎是基于概率的算法的通病。PRM、RRT也都具有这种问题。不过他们三者的具体情况还是有一些不一样。

对于PRM来说，它对狭窄通道表现不佳，是因为在采样过程中，采样到狭窄通道的概率比较低，因而比较难找到经过狭窄通道的路径。

对于RRT来说，它对狭窄通道表现不佳，是因为RRT很难生长进入狭窄通道，毕竟采样——生长，能够生长出来一个位于狭窄通道内的node的概率太低了。

而对于PCD来说，则属于第三种情况，要想用possibly free cell来表示个狭窄通道可能需要重复多轮才能完成，也就是需要好多个小的possibly free cell来表示一个狭窄通道，这导致运行时间过长，效率太低。

引用

[1] Lingelbach F . Path Planning using Probabilistic Cell Decomposition[J]. IEEE, 2004.