一、前言
在平时我们的作业中,我们有可能会遇到对于数组需要进行一个数或者是一批数的插入处理。在这里我们如果采用传统暴力插入的话,每一次插入处理我们都是O(n)的时间复杂度,如果我们插入的次数一旦变多,那么很容易就会超时,在这里我们需要学习一种数据结构----链表。
本篇博客建议与博主另一篇博客一起学习理解(【图论】链式前向星)
二、单链表概念讲解
在链表中,我们依然使用数组来模拟,在数组中,我们有数字在数组中的编号与这个数字本身,如a[3]=7.编号为3,数字为7。但是我们在但链表中我们还需要对于每一个数字加一个变量next,用来储存下一个数字的编号,例如next[3]=9,就代表a[3]的下一个数不是a[4],而是a[9]。
数组:e[N],ne[N]

注意:规定当ne[x]=-1时,x是链表的最后一个元素
在单链表中,还有一个重要的变量head,它代表着当前链表最前面的数字的编号,如果要遍历整条链表,我们就需要从head开始遍历。
没有听懂?这很正常,让我们尝试着通过代码来理解链表。
三、单链表代码讲解
例题链接:Acwing 单链表
实现一个单链表,链表初始为空,支持三种操作:
向链表头插入一个数;
删除第 k 个插入的数后面的数;
在第 k 个插入的数后插入一个数。
现在要对该链表进行 M 次操作,进行完所有操作后,从头到尾输出整个链表。
注意:题目中第 k 个插入的数并不是指当前链表的第 k 个数。例如操作过程中一共插入了 n 个数,则按照插入的时间顺序,这 n 个数依次为:第 1 个插入的数,第 2 个插入的数,…第 n 个插入的数。
输入格式
第一行包含整数 M,表示操作次数。
接下来 M 行,每行包含一个操作命令,操作命令可能为以下几种:
H x,表示向链表头插入一个数 x。
D k,表示删除第 k 个插入的数后面的数(当 k 为 0 时,表示删除头结点)。
I k x,表示在第 k 个插入的数后面插入一个数 x(此操作中 k 均大于 0)。
输出格式
共一行,将整个链表从头到尾输出。
数据范围
1≤M≤100000
所有操作保证合法。
输入样例:
10
H 9
I 1 1
D 1
D 0
H 6
I 3 6
I 4 5
I 4 5
I 3 4
D 6
输出样例:
6 4 6 5
正确代码
//#pragma GCC optimize(2)
#include<iostream>
#include<iomanip>
#include<cstdio>
#include<string>
#include<algorithm>
#include<cmath>
#include<queue>
#include<vector>
#include<map>
#include<stack>
#include<set>
#include<bitset>
#include<ctime>
#include<cstring>
#include<list>
#define ll long long
#define ull unsigned long long
#define INF 0x3f3f3f3f
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
typedef pair<int, int> PII;
const int N = 1e6 + 7;
int head, e[N], ne[N], idx=1; //链表实现的数组,idx代表数的编号
void add_head(int x) //把x加到链表的第一个
{
ne[idx] = head;
e[idx] = x;
head = idx++;
}
void insert(int k, int x) //在第k个元素后插入x
{
e[idx] = x;
ne[idx] = ne[k];
ne[k] = idx;
idx++;
}
void del(int k) //删除第k个元素后一个元素
{
ne[k] = ne[ne[k]];
}
void solve()
{
head = -1; //初始化链表首为-1
int m;
cin >> m;
while (m--)
{
char op;
cin >> op;
if (op == 'H')
{
int x;
cin >> x;
add_head(x);
}
else if (op == 'D')
{
int k;
cin >> k;
if (k == 0)
head = ne[head];
else
del(k);
}
else
{
int k, x;
cin >> k >> x;
insert(k, x);
}
}
for (int i = head;i!=-1;i=ne[i])
{
cout << e[i] << ' ';
}
}
int main()
{
std::ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
solve();
return 0;
}
通过代码还是没有看懂吗?我们来把代码中的函数挑出来解释一下吧。
add_head()函数
void add_head(int x) //把x加到链表的第一个
{
ne[idx] = head;
e[idx] = x;
head = idx++;
}
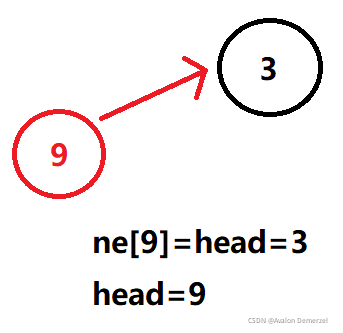
首先我们假设head=3,idx=9,x=5。通过之前的概念介绍,我们可以知道链表的第一个元素的编号是3.
那么我们要把ne[9]设定成head,即现在的链头----3号点,代表3号点变成了9号点的下一个点。然后修改head=9,代表现在链头为9号点了!
接着设置e[9]=5,代表9号点的值为5.
insert()函数
void insert(int k, int x) //在第k个元素后插入x
{
e[idx] = x;
ne[idx] = ne[k];
ne[k] = idx;
idx++;
}
首先我们假设现在的链表为这样的,idx为即将插入的元素
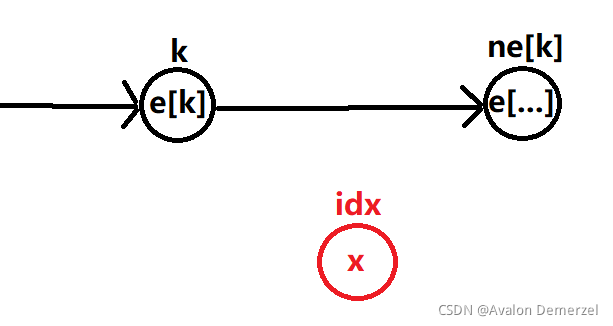
在执行完ne[idx] = ne[k]; ne[k] = idx;操作后,链表就变成了这样
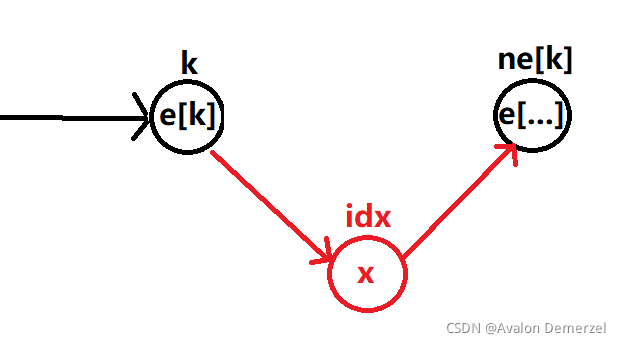
一定要注意上面两条代码的执行顺序,否则…你自己对着图试试看?
del()函数
理解了上面的insert函数后,del函数的理解就非常简单了
void del(int k) //删除第k个元素后一个元素
{
ne[k] = ne[ne[k]];
}
画一张图来理解吧
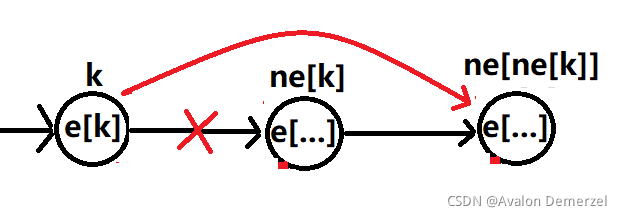
这样实际上就达到了删除操作的效果了。
四、双链表
如果能够完全理解单链表的话,那么双链表也就不难理解了
相比单链表,双链表把next数组变成了左右两个数组L[N],R[N]。这样我们就可以查到一个数的左右两个数的编号。
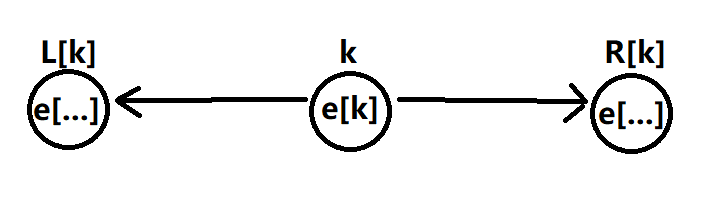
在双链表初始化的过程中,我们人为设定编号为0和1的点,作为链表的最左和最右的的点方便操作。具体步骤见下方例题代码讲解

例题链接:Acwing 双链表
实现一个双链表,双链表初始为空,支持 5 种操作:
在最左侧插入一个数;
在最右侧插入一个数;
将第 k 个插入的数删除;
在第 k 个插入的数左侧插入一个数;
在第 k 个插入的数右侧插入一个数
现在要对该链表进行 M 次操作,进行完所有操作后,从左到右输出整个链表。
注意:题目中第 k 个插入的数并不是指当前链表的第 k 个数。例如操作过程中一共插入了 n 个数,则按照插入的时间顺序,这 n 个数依次为:第 1 个插入的数,第 2 个插入的数,…第 n 个插入的数。
输入格式
第一行包含整数 M,表示操作次数。
接下来 M 行,每行包含一个操作命令,操作命令可能为以下几种:
L x,表示在链表的最左端插入数 x。
R x,表示在链表的最右端插入数 x。
D k,表示将第 k 个插入的数删除。
IL k x,表示在第 k 个插入的数左侧插入一个数。
IR k x,表示在第 k 个插入的数右侧插入一个数。
输出格式
共一行,将整个链表从左到右输出。
数据范围
1≤M≤100000
所有操作保证合法。
输入样例:
10
R 7
D 1
L 3
IL 2 10
D 3
IL 2 7
L 8
R 9
IL 4 7
IR 2 2
输出样例:
8 7 7 3 2 9
正确代码
//#pragma GCC optimize(2)
#include<iostream>
#include<iomanip>
#include<cstdio>
#include<string>
#include<algorithm>
#include<cmath>
#include<queue>
#include<vector>
#include<map>
#include<stack>
#include<set>
#include<bitset>
#include<ctime>
#include<cstring>
#include<list>
#define ll long long
#define ull unsigned long long
#define INF 0x3f3f3f3f
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
typedef pair<int, int> PII;
const int N = 1e6 + 7;
int L[N], R[N], e[N], idx; //用来实现双链表
void init() //初始化函数
{
L[0] = 1;//右节点0
R[1] = 0;//左节点1
idx = 2;
}
void insert(int k, int x) //在第k个点后插入x
{
e[idx] = x;
R[idx] =R[k];
L[idx] = k;
L[R[k]] = idx;
R[k] = idx;
idx++;
}
void del(int k) //删除函数
{
R[L[k]] = R[k];
L[R[k]] = L[k];
}
void solve()
{
init();
int m;
cin >> m;
while (m--)
{
string op;
cin >> op;
if (op == "L")
{
int x;
cin >> x;
insert(1, x);
}
if (op == "R")
{
int x;
cin >> x;
insert(L[0], x);
}
if (op == "D")
{
int k;
cin >> k;
del(k+1);
}
if (op == "IL")
{
int k, x;
cin >> k >> x;
insert(L[k+1], x);
}
if (op == "IR")
{
int k, x;
cin >> k >> x;
insert(k+1, x);
}
}
for (int i = R[1]; i != 0; i = R[i]) //链表的遍历
{
cout << e[i] << ' ';
}
}
int main()
{
std::ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
solve();
return 0;
}
如果代码有地方不太好理解的话,画个图看看也许是一个不错的选择哦。
作者:Avalon Demerzel,喜欢我的博客就点个赞吧,更多图论与数据结构知识点请见作者专栏《图论与数据结构》