[数据结构与算法]带你图解二叉树的多种递归遍历（建议收藏！！）

二叉树的构建

为了实现二叉树的遍历，我们要先构建一个二叉树，这里就先简单构建一个。

结点类型的定义

既然是链式二叉树，那必须得有自己的结点类型，以下是链式二叉树结点类型的定义

typedef char BTDataType;
typedef struct BinaryNode
{
	BTDataType x;
	struct BinaryNode* left;
	struct BinaryNode* right;
}BT;

构建二叉树之间的关系

BT* BuyNode(BTDataType x)
{
	BT* new = (BT*)malloc(sizeof(BT));
	if (new == NULL)
	{
		printf("malloc failed\n");
		exit(-1);
	}
	new->x = x;
	new->left = NULL;
	new->right = NULL;
	return new;
}

void BinaryCreat()
{
	BT* n1 = BuyNode('A');
	BT* n2 = BuyNode('B');
	BT* n3 = BuyNode('C');
	BT* n4 = BuyNode('D');
	BT* n5 = BuyNode('E');
	BT* n6 = BuyNode('F');
	n1->left = n2;
	n1->right = n3;
	n2->left = n4;
	n3->left = n5;
	n3->right = n6;
}

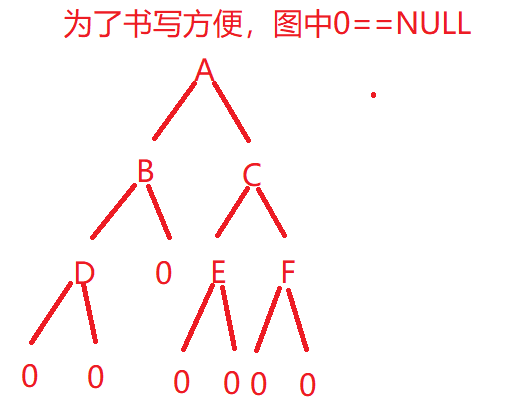
构建完之后的二叉树是这个样子的：

深度优先遍历

二叉树的深度优先遍历有以下三种

前序遍历

前序遍历，又叫先根遍历。
遍历顺序：根 -> 左子树 -> 右子树

代码实现

void BinaryPrev(BT* n1)
{
	if (n1==NULL)
	{
		printf("NULL ");
		return ;
	}
	printf("%c ", n1->x);
	BinaryPrev(n1->left);
	BinaryPrev(n1->right);
}

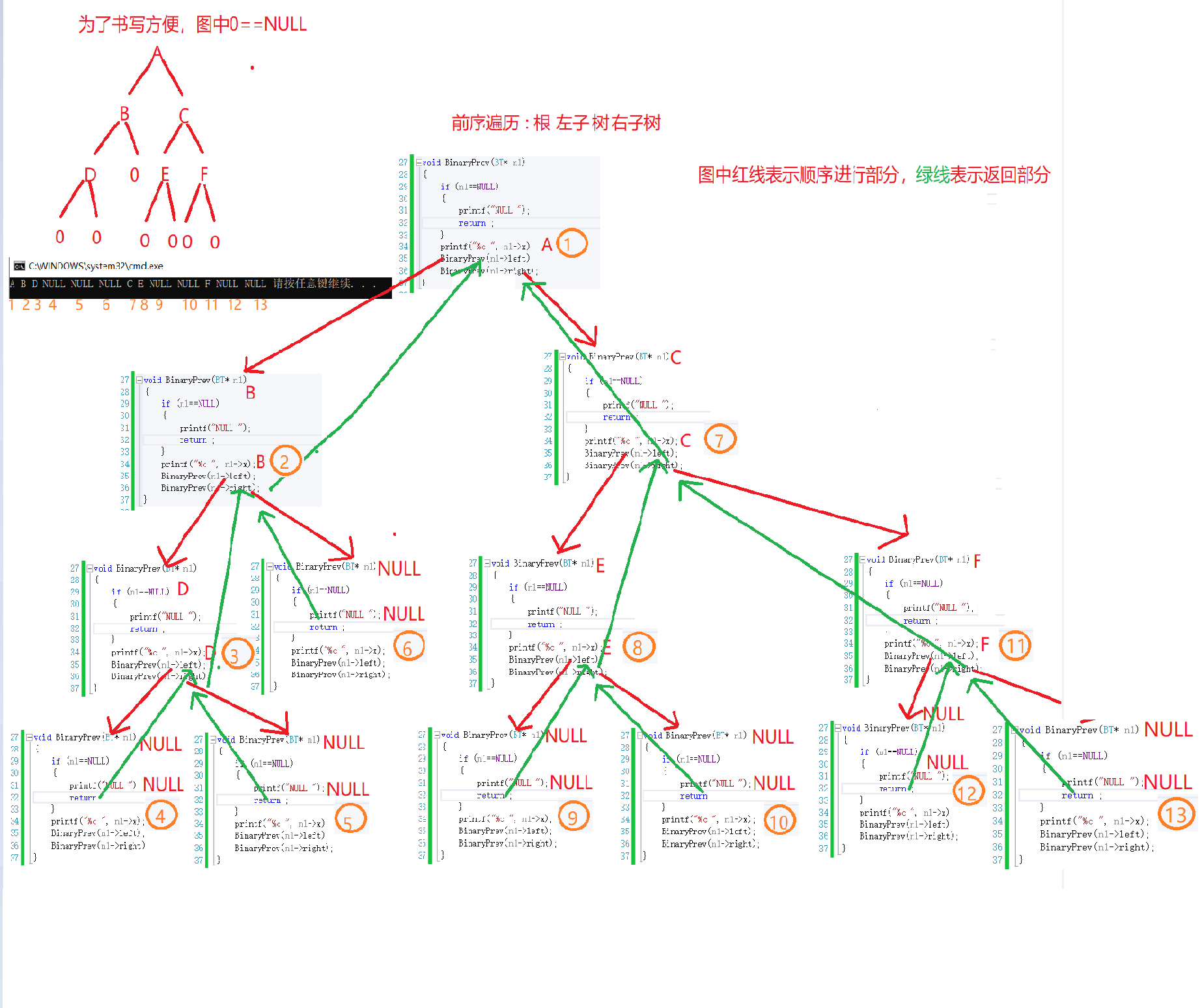
很多小伙伴可能会觉得：哇！这么少的代码就可以解决了吗？对，就是这么几行，这也就是递归遍历的强大之处。但是这之间的递归过程是很复杂的。

图解递归（由于图片大小问题，建议用手机客户端查看，以下图解也是）

中序遍历

中序遍历，又叫中根遍历。
遍历顺序：左子树 -> 根 -> 右子树

代码实现

void MiddleOrder(BT* n1)
{
	if (n1 == NULL)
	{
		printf("NULL ");
		return;
	}
	MiddleOrder(n1->left);
	printf("%c ", n1->x);
	MiddleOrder(n1->right);
}

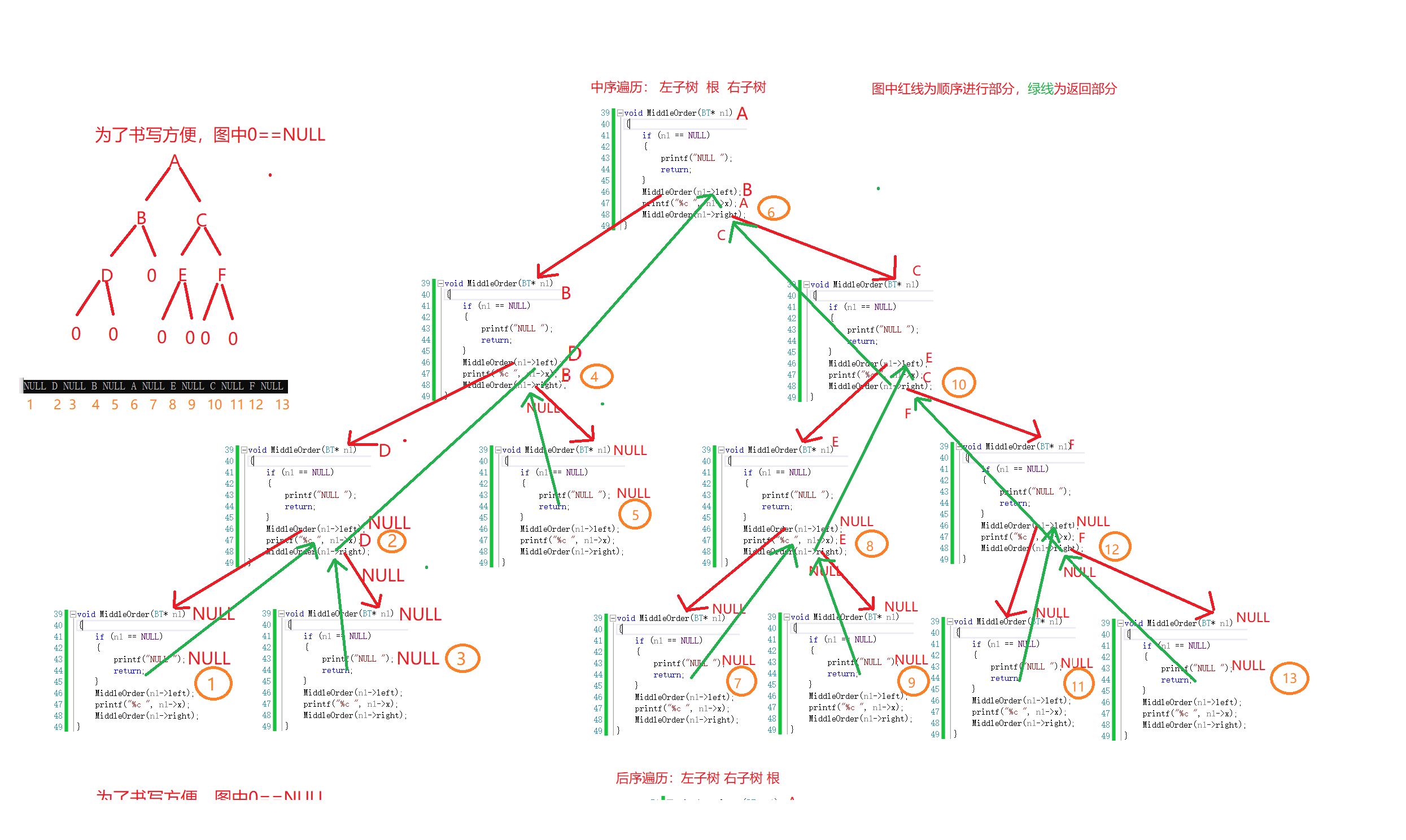
这个也是同样的简单，只要按着它的顺序写就行了，但其中的过程很复杂。

图解递归

后序遍历

后序遍历，又叫后根遍历。
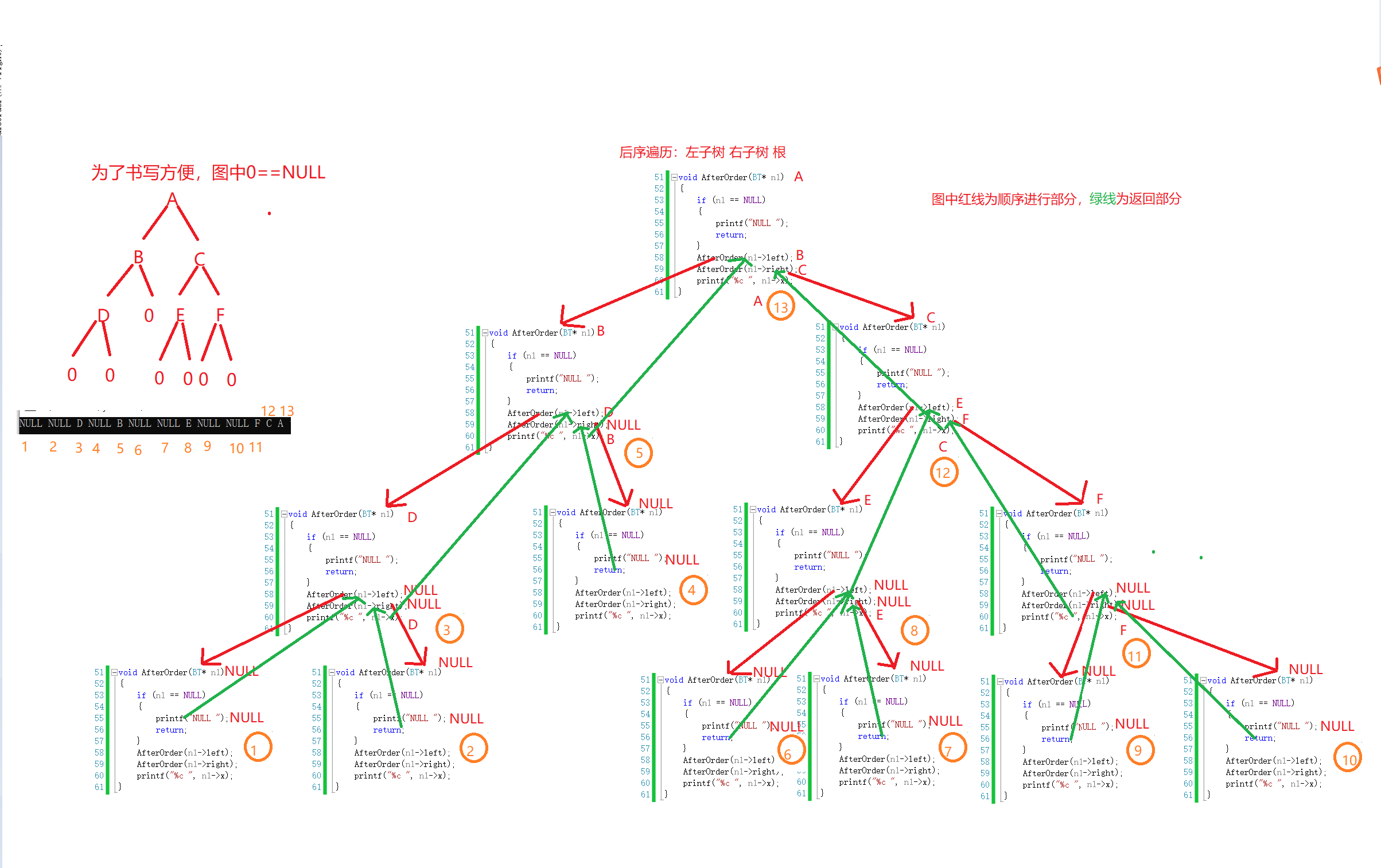
遍历顺序：左子树 -> 右子树 -> 根

代码实现

void AfterOrder(BT* n1)
{
	if (n1 == NULL)
	{
		printf("NULL ");
		return;
	}
	AfterOrder(n1->left);
	AfterOrder(n1->right);
	printf("%c ", n1->x);
}

这个同样也是只要按着顺序写就可以了，递归起来很复杂。

图解递归

广度优先遍历

层序遍历

层序遍历，自上而下，从左往右逐层访问树的结点的过程就是层序遍历。

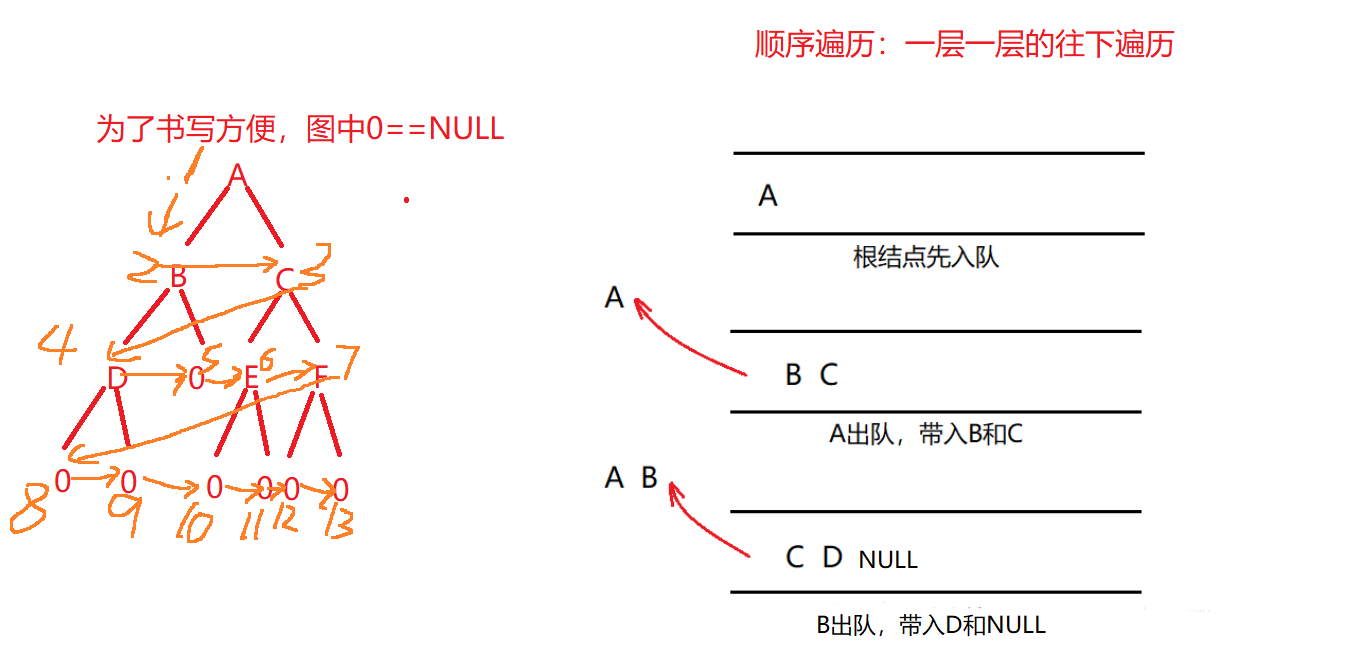
思路（借助一个队列）：
1.先把根入队列，然后开始从队头出数据。
2.出队头的数据，把它的左孩子和右孩子依次从队尾入队列（NULL不入队列）。
3.重复进行步骤2，直到队列为空为止。

代码实现

在实现过程中要用到队列，具体队列的实现这儿就不说了，博主之前的博客中有相关的文章。

void BinaryLevelOrder(BT* n1)
{
	Queue q;
	QueueInit(&q);
	if (n1!=NULL)
	{
		QueuePush(&q, n1);
	}
	while (!QueueEmpty(&q))
	{
		BT* front = QueueTop(&q);
		QueuePop(&q);
		printf("%c ", front->x);
		// 不把NULL打印出来
		//if (front->left!=NULL)
		//{
		//	QueuePush(&q, front->left);
		//}
		//if (front->right != NULL)
		//{
		//	QueuePush(&q, front->right);
		//}
		if (front->left != NULL)
		{
			QueuePush(&q, front->left);
		}
		else
		{
			printf("NULL ");
		}
		if (front->right != NULL)
		{
			QueuePush(&q, front->right);
		}
		else
		{
			printf("NULL ");
		}

	}
	QueueDestory(&q);
}