普通递归思路
背包最多装6公斤,现有3件物品
| 1 | 2 | 3 | |
|---|---|---|---|
| 重量 | 2 | 3 | 4 |
| 价格 | 1 | 3 | 5 |
求背包能装下的最大价值?
首先我们回到小学,把它看成一道智力题,我们会用下图的方法解决。就是从6开始每次都有三个选择,选择后继续用剩下的重量选择,比如6公斤选了1号物品,那么接下里用4公斤的去做选择,以此类推,最后我们把得到的结果比较,得到5为结果。
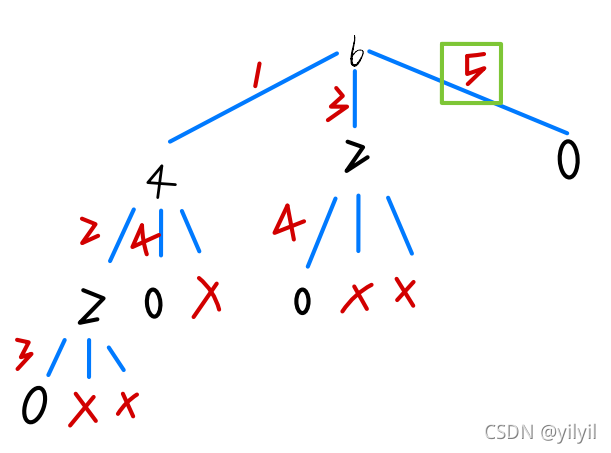
那么我们使用计算机解决问题,也是类似,告诉计算机选择,以及比较大小:
选择
- 选择 1 :(1+ 4公斤)
- 选择 2 :(3+ 2公斤)
- 选择 3: (5+ 0公斤)
比较:max[(1+ 4公斤),(3+ 2公斤),(5+ 0公斤)]
对4公斤选择
- 选择 1 :(2+ 2公斤)
- 选择 2 :(4+ 0公斤)
- 选择 3: 不行
比较:max[(2+ 2公斤),(4+ 0公斤)]
这就是我们很朴素的递归解决问题的思路
dp[i]=max[ (v[j]+ dp[i-w[j])]
dp[i]:第i公斤能装载的最大价值
w[j]:第j件物品的重量
v[j]:第j件物品的价值
动态规划如何想到的
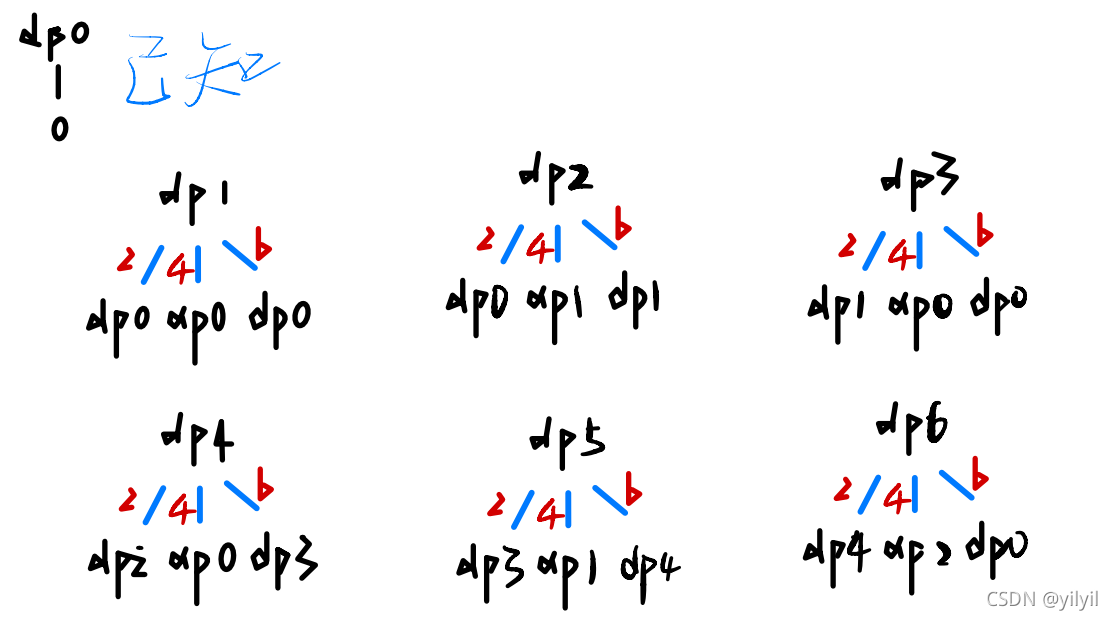
在上面我们发现,6公斤的背包 依赖4公斤和2公斤能装下的最大价值,那么我们就可以先解决4公斤和2公斤的问题,也就是将自顶向下变为自底向上,并且我们发现2公斤我们算了两遍,自底向上可以很好的复用子问题的结果
 所以我们就能
所以我们就能
dp[0]=0
dp[1]=0
dp[2]=max[dp[2-1]+2, , ]=1
…
dp[6]=max(dp[4]+1,dp[2]+3,dp[0]+5)=5
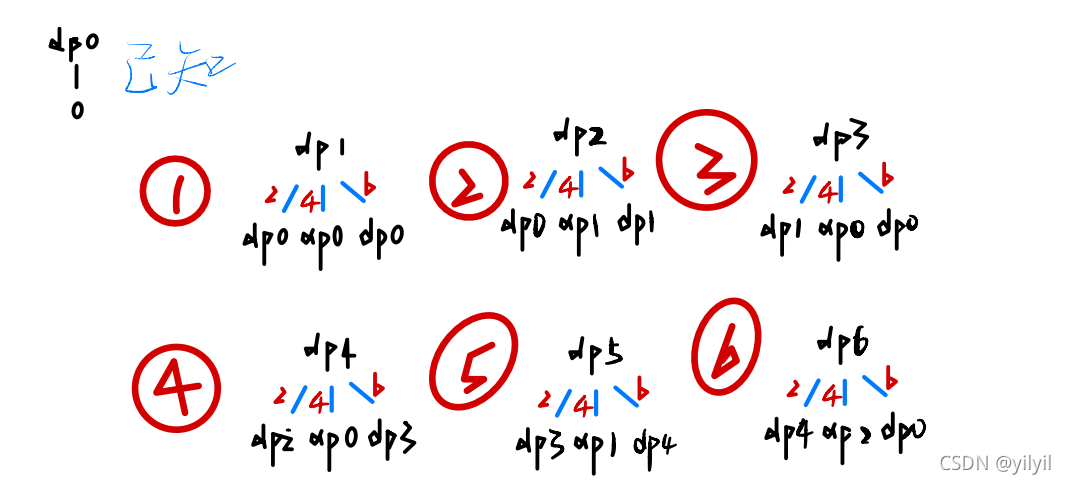
过程如下
总结:
横向dp表格与纵向dp表格的区别
思路:x公斤背包的装某件w公斤物品 分为装得下(w<=x)和根本装不下(w>x)
而装得下我们就可以选择装(涉及将背包某些位置腾出来)还是不装,这就根据装和不装结果的大小
上面画了6个dp树状图,可以化为表格:
横向
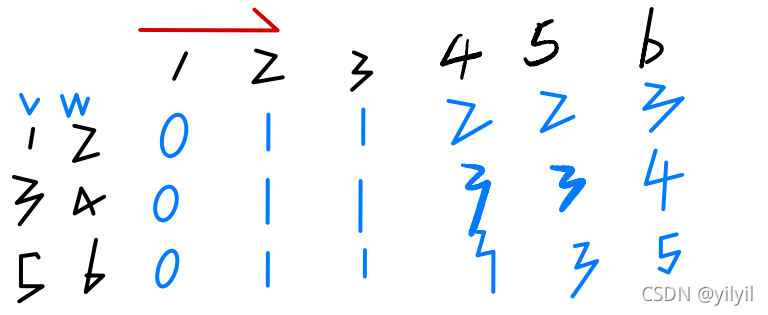
横向是固定物品件数,更换重量,三趟,可以把步骤变为下

纵向
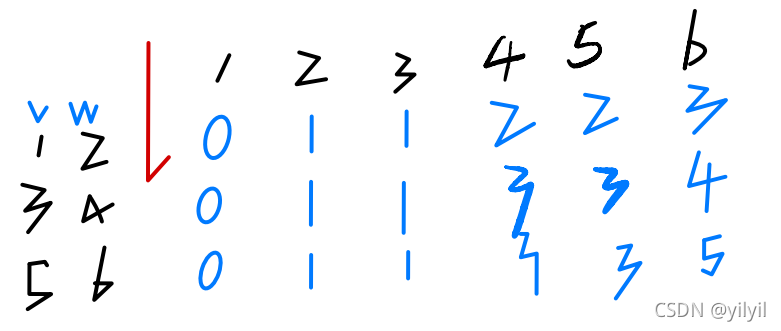
纵向是固定重量,更换物品件数,6趟 可以把步骤拆分如下
总结
我们使用递归总结dp表达式,使用自底向上写代码
题型总结
用重量装满背包,价值最大
用票时装满行程,票价最小 983. 最低票价
用硬币装满额度,数量最少 322. 零钱兑换