因为对于这些排序算法,网上确实已经有很多图文并茂的讲解了,所以在此就不过多的解释,仅记录一下三种算法的实现和对比
一、快速排序
import java.util.Random;
public class QuickSort {
private static Random random = new Random();
private static void quickSort(int[] nums, int l, int r) {
if (l < r) {
int pos = partition(nums, l, r);
quickSort(nums, l, pos - 1);
quickSort(nums, pos + 1, r);
}
}
private static int partition(int[] nums, int l, int r) {
int index = random.nextInt(r - l + 1) + l; // 随机选一个作为中心
swap(nums, r, index);
int pivot = nums[r];
int i = l - 1;
for (int j = l; j < r; ++j) {
if (nums[j] <= pivot) {
++i;
swap(nums, i, j);
}
/*
降序版本:将nums[j] <= pivot改为nums[j] >= pivot
*/
}
swap(nums, i + 1, r);
return i + 1;
}
private static void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
public static void main(String[] args) {
int[] nums = new int[]{4, 1, 2, 7, 9, 6, 8, 5, 3};
quickSort(nums, 0, nums.length - 1);
for (int num : nums) {
System.out.println(num);
}
}
}?这里采用随机数的方法来避免已排序数组导致快排递归深度过深的问题
二、堆排序
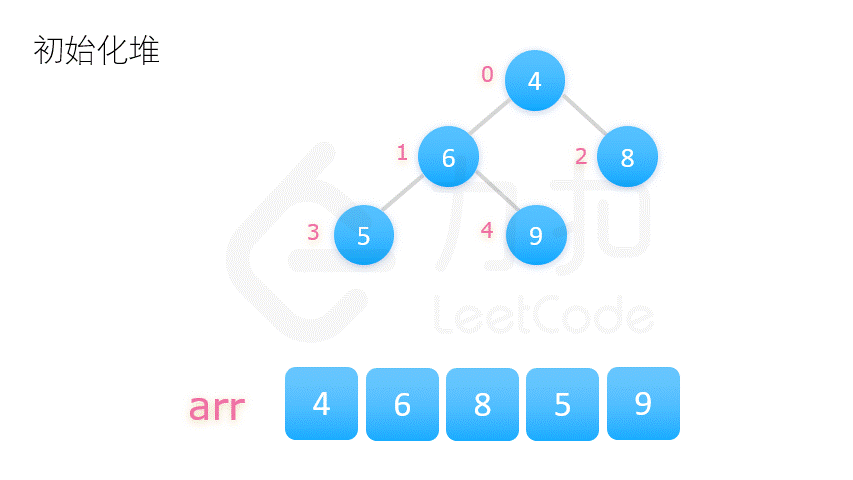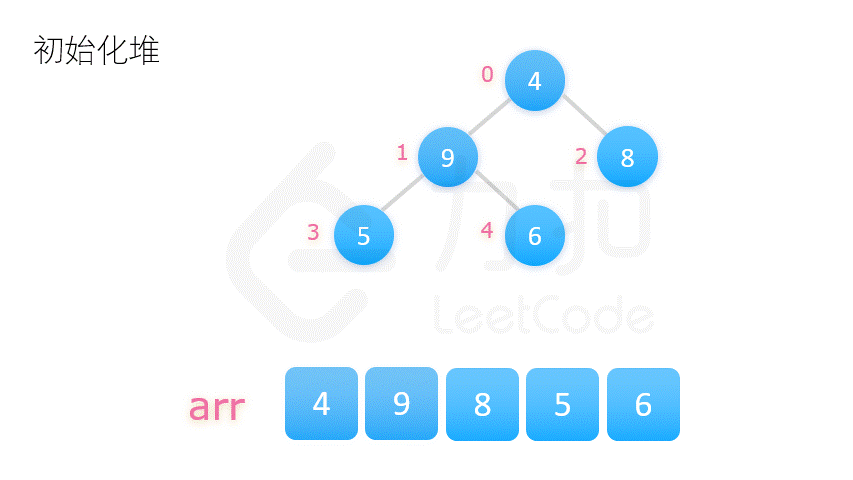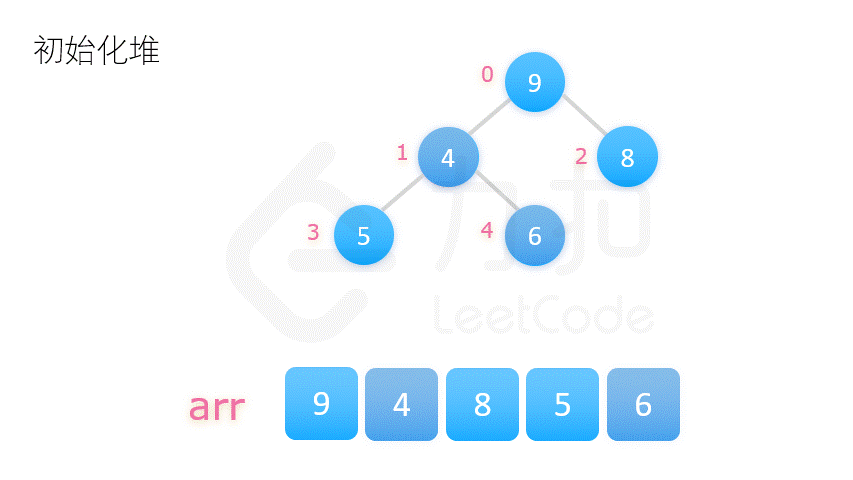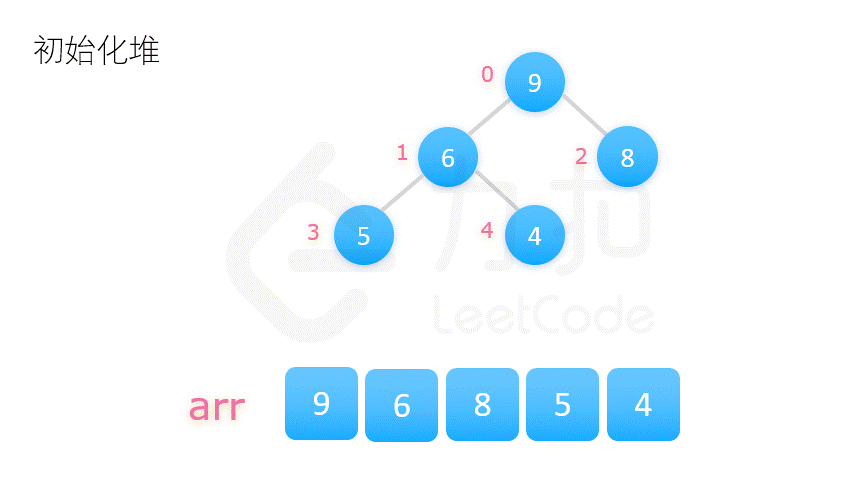
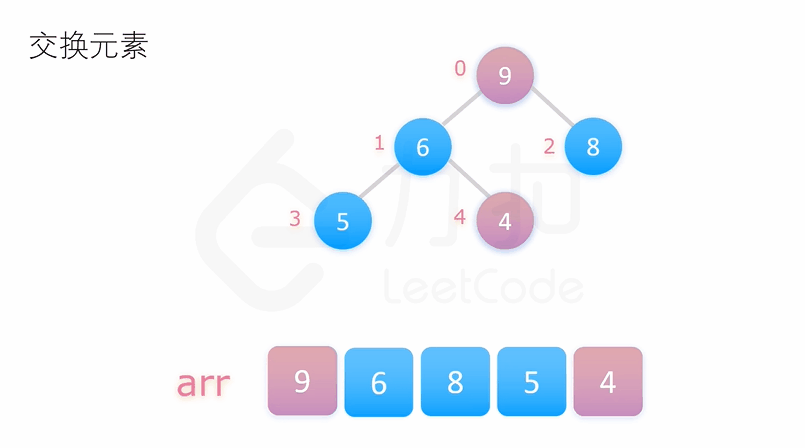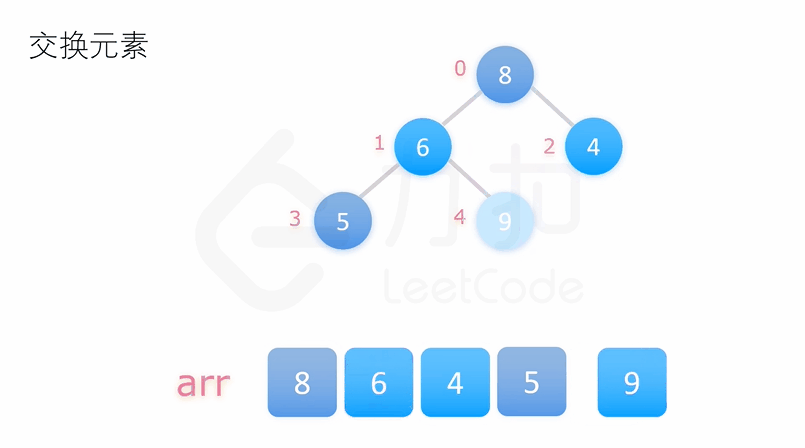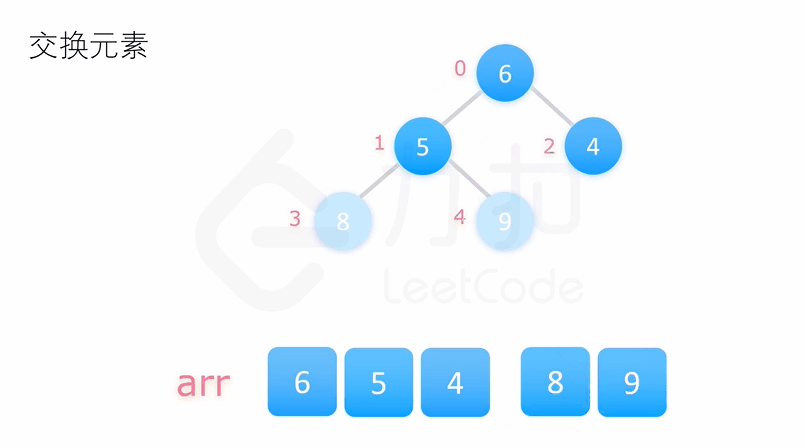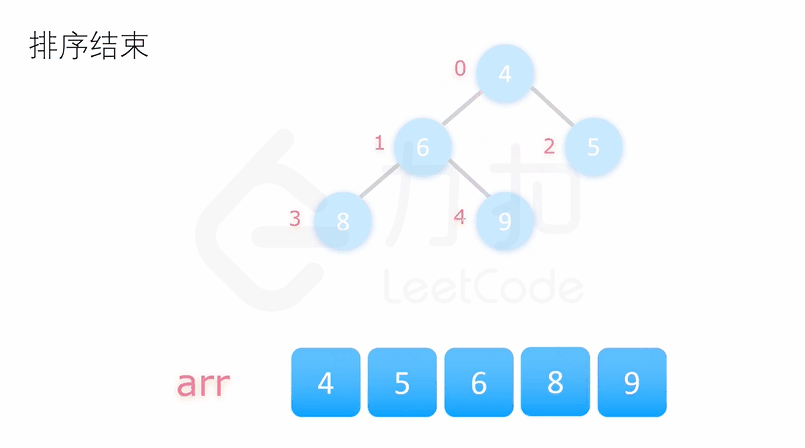
public class HeapSort {
private static void heapSort(int[] nums) {
// 创建堆
int len = nums.length;
for (int i = (len - 1) / 2; i >= 0; --i) {
// 从第一个非叶子结点从下至上,从右至左调整结构
adjustHeap(nums, i, len);
}
// 交换堆顶元素与末尾元素 并 调整堆结构
for (int i = len - 1; i > 0; --i) {
// 将堆顶元素与末尾元素进行交换
swap(nums, i, 0);
// 重新对堆进行调整
adjustHeap(nums, 0, i);
}
}
private static void adjustHeap(int[] nums, int parent, int len) {
// 用temp记录父节点的值
int temp = nums[parent];
int lChild = 2 * parent + 1;
while (lChild < len) {
int rChild = lChild + 1;
// 如果有右孩子结点,并且右孩子结点的值大于左孩子结点,则选取右孩子结点
if (rChild < len && nums[lChild] < nums[rChild]) {
++lChild;
}
// 如果父结点的值已经大于孩子结点的值,则直接结束
if (temp >= nums[lChild]) {
break;
}
/*
降序版本:将上两个if语句替换如下
if (rChild < len && nums[lChild] > nums[rChild]) {
++lChild;
}
if (temp <= nums[lChild]) {
break;
}
*/
// 把孩子结点的值赋给父结点
nums[parent] = nums[lChild];
// 选取孩子结点的左孩子结点,继续向下筛选
parent = lChild;
lChild = 2 * lChild + 1;
}
nums[parent] = temp;
}
private static void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
public static void main(String[] args) {
int[] nums = new int[]{4, 1, 2, 7, 9, 6, 8, 5, 3};
heapSort(nums);
for (int num : nums) {
System.out.println(num);
}
}
}
// 参考:https://www.cnblogs.com/luomeng/p/10618709.html
三、归并排序
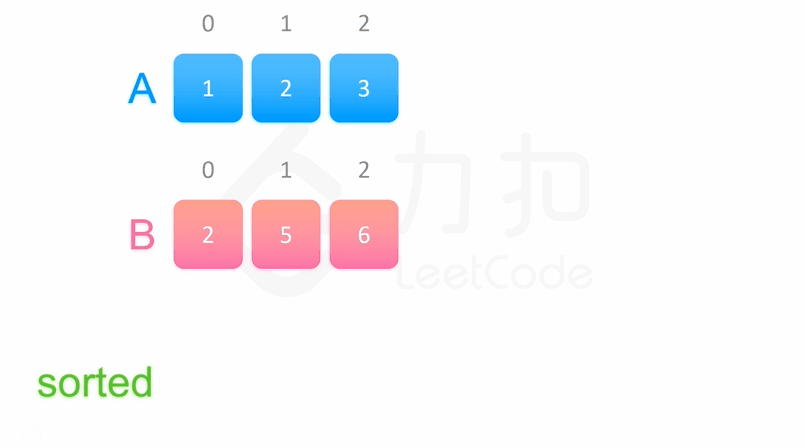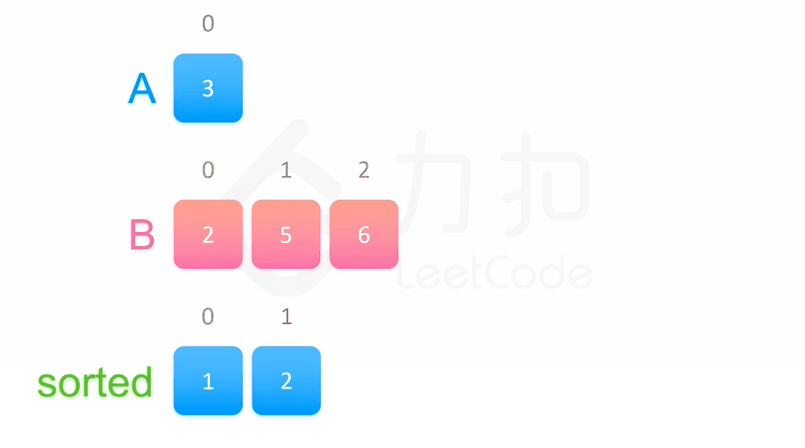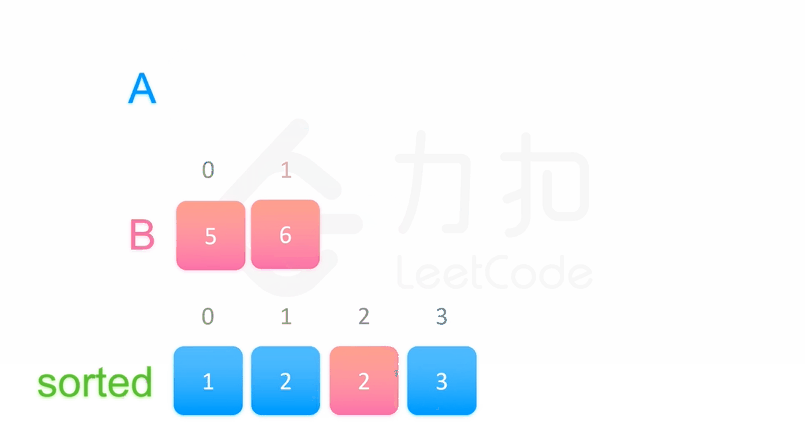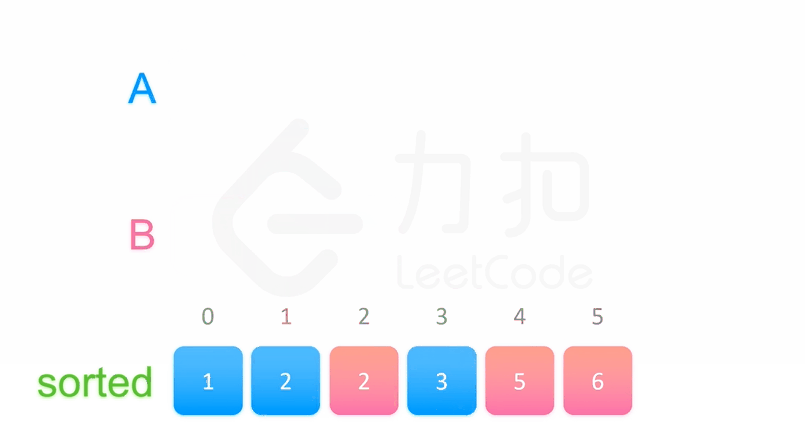
public class MergeSort {
private static int[] temp;
private static void mergeSort(int[] nums, int l, int r) {
if (l >= r) {
return;
}
int mid = (l + r) / 2;
mergeSort(nums, l, mid);
mergeSort(nums, mid + 1, r);
int i = l, j = mid + 1;
int count = 0;
while (i <= mid && j <= r) {
if (nums[i] < nums[j]) {
temp[count++] = nums[i++];
} else {
temp[count++] = nums[j++];
}
/*降序版本:将nums[i] < nums[j]改为nums[i] > nums[j]*/
}
while (i <= mid) {
temp[count++] = nums[i++];
}
while (j <= r) {
temp[count++] = nums[j++];
}
for (int k = 0; k < r - l + 1; ++k) {
nums[k + l] = temp[k];
}
}
public static void main(String[] args) {
int[] nums = new int[]{4, 1, 2, 7, 9, 6, 8, 5, 3};
temp = new int[nums.length];
mergeSort(nums, 0, nums.length - 1);
for (int num : nums) {
System.out.println(num);
}
}
}四、对比
| 排序方法 | 时间复杂度 | 空间复杂度 | 稳定性 | 使用场景 |
| 快速排序 | O(nlogn) | O(h)(h为递归深度) | 不稳定 | 时间要求高,但不要求稳定性 |
| 堆排序 | O(nlogn) | O(1) | 不稳定 | 空间要求高 |
| 归并排序 | O(nlogn) | O(n) | 稳定 | 要求稳定性 |