引言
这是最优化的内容,我们用状态(包含很多参数)描述一个对象。把这些参数作为坐标轴就会获得一个超空间(函数定义域)。超空间里的点分别对应了某个函数值,我们在空间里找函数的最大值。
后面会介绍各种算法,但是核心是找上一节课的h(n)——一个描述状态分数的函数。
局部搜索算法
所谓局部就是只关心状态,不关心路径,从一个点到其他点。
爬山法
就是梯度下降法,只不是找最大值。就是找参数在状态空间临近区域的最优解。相信大家都会。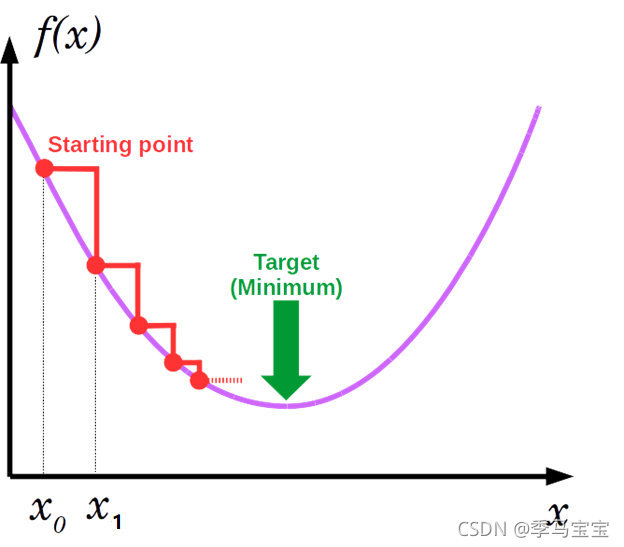
显然有很多时候无法找到全局最优解。
比如到了一个平坦的区域,往哪个方向最大值都不会变化,这时候可以有随机爬山法,比如说随机选择后继直到上升。
但这样也不行,可能会被困在局部最优解。可以采用这样一种方式,随机生成一个初始点,爬山法找到解的概率为p,那么重复进行1/p次爬山法,基本可以找到最优解。也就是反复随机生成初始点进行爬山。
模拟退火
给一个初始点,在他周围随机找点,如果比他更优则更新到这个点,否则以概率p接收这个点,每次接受“更差”的点时,p的值以指数下降。
我这里记录一下我对这个算法的理解
如果使温度(接收概率)下降够慢,找到全局最优解的概率区域1
我们考虑特殊情况,如果我的温度不下降,始终以百分之五十的概率接收,也就是存粹的随机算法,那么在时间趋于无穷时,一定会找到全局最优解。但是事实上我们并没有无限次尝试的机会,我们必须让结果收敛,这种操作会使得找到全局最优解的可能性降低,但是性能大大提高。
时间和精准程度处在一种矛盾的平衡当中,将这个概率从1降低到0.999,但是却可以使得时间消耗从无限变为有限。模拟退火可以说是完全随机的一种妥协。
局部束搜索
随机选择k个点,搜索所有k个点生成的状态,取最好的k个,重复此过程。这和遗传算法有点像,但是没有k个点之间的交叉,所以是无性繁殖。
遗传算法
随机生成k个状态,给状态编码,然后用某种算法(最简单交换一部分),然后会得到很多新的状态作为“孩子”,从这些“孩子”中选k个最好的,重复过程。
说得简单,具体比较复杂,但是思想比较容易理解。
连续空间中的局部搜索
连续空间的搜索难度在于每种状态接下来的分支是无限的。基本的思想还是梯度法,但是由于自变量多,方程的梯度=0无法求出封闭式解(就是列的方程没有通解,每次都要经过数值推理),但是可以使用局部梯度(对某个参数求导),然后沿着这个方向爬。
也有更快的爬法,这些可以去看最优化算法,什么牛顿法、共轭梯度法、拟牛顿法啥的,有空再整理一下。
使用不确定动作搜索
在同样的条件下,一个状态可能转移为多个状态。那么整个过程不再是一棵树,而是一个序列。
就像你开车,大路短但可能堵车,小路长但是比较通畅。你的决策产生的结果还依赖于你不可观测的外在条件。这种时候你的策略也被叫做应急策略。
通常来说,我们想要找的是一个稳定可以达到目标的解,我们最终的解应该是一棵树,无论在树的分叉路口如何走,最终都会到达满足的状态点。
还是普通的搜索,只不过一个需要抉择的节点,需要在所有子树中都找到解,这个点才能在最后的解答中。
由于搜索过程中会出现循环,你可以把它理解成一棵无限生长的树(或者一张有环图)。在搜索树的过程中把状态hash,如果遇到相同的状态就是遇到循环,也不需要再继续搜索了。
使用部分可观察信息搜索
- 先是无观察信息搜索
即便我根本不知道自己身处什么状态,也可以找出最好的决策。
来波很不恰当的但是我相信很能说明问题的例子。你肚子疼,你应该去做身体检查,然后确定自己吃什么药。但是你怕检查完你直接痛死了,于是你吃了所有治疗肚子疼的药,然后你也不知道,总之有一个药让你肚子不疼了。
这个例子当然是在胡说八道,但是却告诉我们,即便我们根本不知道处在什么状态,也可能做出走到目标点的决策。
比如说状态(1,1,0)代表得了病1、2,没有病3,那么所有状态一共有8种,但是通过吃所有药都可以变为(0,0,0)的状态。
求解方法比较魔幻,因为状态太多了。可以先求解满足一个状态的路径,然后一个个看这些路是不是满足其他状态;也可以把这些状态统一打包编码不管内部情况;或者使用巧妙的动态状态描述,比如说一个药吃了能治疗某四种病,不用(0,0,0,0)表述,而是直接打包成一种某类病0。
- 然后是可观察搜索/部分观察
我慢慢觉得没啥好写的,无非是状态定义和转移的问题,我越来越觉得这本书只可意会不可言传。
联机搜索问题
失去上帝视角,走一步看一步。我(智能体)出生在了一个迷宫中,我现在要出去,我只有前后左右四个方向可以走,和一个标志和我位置的传感器,但我不知道迷宫长什么样子。
还是一棵树,但是只有到了某个节点才能看到之后的节点,那显然就是一个一直回朔的过程。最差情况每个点要走两次(dfs)
- 随机行走算法
爬山法,这回是真爬山,爬到了一个小坡上面(局部最优)。按之前的再随机一个出生点再爬,但是不行,因为这是真爬山。那我就随便走走,往右走走虽然变低了但是却可以看到一座可能更高的山(启发式函数h(n)这里我当作目测山高),那我就会往那里走。
总结
我发现这门课越来越玄学,真的全靠感受。给的都只是思想,细节实现要靠自己,也要根据实际问题。