[数据结构与算法]字符串哈希bkdrhash原理及C语言实现

#主要资料参考：
https://blog.csdn.net/wanglx_/article/details/40400693?spm=1001.2014.3001.5501
https://blog.csdn.net/WhereIsHeroFrom/article/details/119838427?spm=1001.2014.3001.5506

要在学生管理系统中用到hash以提高查询速度，因此需要用到hash算法。经过查询，比较好用的字符串hash有bkdrhash，网上也有比较好的解析，因此选用这个算法进行应用。
首先简单回顾一下哈希及其算法。

哈希函数

Hash，一般翻译做散列、杂凑，或音译为哈希，是把任意长度的输入（又叫做预映射pre-image）通过散列算法变换成固定长度的输出，该输出就是散列值。这种转换是一种压缩映射，也就是，散列值的空间通常远小于输入的空间，不同的输入可能会散列成相同的输出，所以不可能从散列值来确定唯一的输入值。简单的说就是一种将任意长度的消息压缩到某一固定长度的消息摘要的函数。 ——百度百科

如果简单来说，哈希是一个函数，我们令其为hash()，对于任意键值key，hash(key)会得到一个值value，这个value有几个性质[1]：

• 确定性：对于不同的value，必定对应着不同的key
• 散列碰撞(collision)：如果value相同，对应的key可能相同，也可能不同。一个好的哈希函数应当尽量让一个value对应一个key
• 不可逆性：就如上述所说，value对应明文（key）理论上不止一个，因此无法从value得到唯一的key

这个有点像高中所学的映射的概念，hash就是一个非双射的映射，由输入对应唯一的输出，但是输出无法对应唯一输入。一个好的hash函数应当向双射靠近。哈希函数多对一”（高中教映射时这么说的）的映射，正显示了它的压缩特性。
哈希函数有不同的实现方法，如直接定址法，除数留余法等等。
由于本文主要介绍bkdrhash算法，因此对于哈希表基本的介绍并不会太详细，希望了解哈希原理的读者可以去：https://blog.csdn.net/WhereIsHeroFrom/article/details/119838427?spm=1001.2014.3001.5506这里面的内容很详细，可以很好的了解哈希的原理。

哈希表

哈希表正是利用了哈希函数的映射效果。它是根据键值直接访问内存地址中的数据的一种数据结构。一般来说，哈希表是一种线性表，在C语言中，数组正是一种线性表，所以哈希表可以通过数组去实现。
通过将键值key转换为一个指针数组的下标，这正是哈希表在C语言中的实现方式。key转为一个下标（整型变量），是通过哈希函数hash去实现的。
一个好的哈希表进行搜索，时间复杂度应为O(1)，亦即value与key形成一 一对应的关系，输入一个键值直接查询到数据所对应的地址。但是，实际上再好的哈希算法也无法保证做到这种效果，从而引发所谓的哈希冲突。

哈希冲突

由于哈希函数无法一对一的情况不可避免，哈希冲突的出现也是不可避免的的。简单来说，哈希冲突就是key1=key2，而hash(key1) = hash(key2)的情况。如果我们要使用单纯的哈希对应地址的方法，便无法表示出两个key值。因此，需要有一种方法去解决哈希冲突。一般来说，解决哈希冲突有几种方法：

• 开放定址法
• 再散列函数法
• 链地址法
• 公共溢出区法

在这里稍微介绍一下链地址法。

这张图片转自https://blog.csdn.net/WhereIsHeroFrom/article/details/119838427?spm=1001.2014.3001.5506，作者英雄哪里出来。比较形象地说明了链地址法如何使用。对于单向链表来说（图中显示的似乎是双向链表，我按照我的理解来讲述），数组储存的仅仅头节点，在插入数据时，检查头节点后的节点是否为空，若为空，则向头节点后插入节点，若为非空，则在尾部插入节点。这样子一个hash值就可以对应多个key值，解决了哈希冲突的问题。
但是，我们可以发现，如果发生哈希冲突，对于冲突部分的查找复杂度不再是O(1)了，因此，我们应该设计好的算法，让它尽量不发生哈希冲突。

这里就引入了针对字符串的哈希算法了，其中bkdrhash是一种比较好的算法。

bkdrhash

对于字符串的哈希函数，比较朴素的想法是将字符串中每个字符的ASCII码相加，然后得到一个数字作为数组的下标。
$"as"=97+115=212$
$"bc"=98+99=197$
可以看到，这种方法确实可以将不同的字符串映射为不同的数字。但是，这个方法存在一个问题，我们看以下的例子。
$"as"=97+115=212$
$"br"=98+114=212$
不同的字符串映射到了同一个哈希值上。发生这种问题的根本原因就是，哈希表的容量远远小于字符串组合的可能性！我们以24个字母组成两个字符串为例。
$24^2=576?47=(24?2?2+1)$
随着字符串数量的增多，两者的差距大概率也会随之增大，意味着哈希冲突的概率也会越来越大，因此，这并不是一个好的哈希函数。
我们应该想到，如何去增加哈希表的大小。
有一个方法便是将每一位乘一个系数，这样子既增加了哈希表的大小，也扩大了字符串每一位的差异，可以更好地避免哈希冲突。
可是，这仍然不太够。
随着字符串位数的增加，可能性的增加并不一定是一个线性的变化，而是一个指数的变化。如果单纯的使用系数，对于位数增长到一定程度的适应并不好。
所以我们很自然地会想到应用幂的方法，对于不同位数采用不同的指数，使得不同位数的权重不同，也避免了字符串内容相同，排列从不同造成哈希值相同的情况。
$"BC"=82\times 2^0+83\times 2^1=248$
$"AD"=81\times 2^0+84\times 2^1=249$
$"DA"=84\times 2^0+81\times 2^1=246$
可以看到，原本用之前的算法是一样的字符串，在这种算法中被分开了。
这便是bkdrhash的核心思想。
bkdrhash算法对于底数的选择很有讲究，因为一些计算机（语言）的特性，选择以2等偶数为底数会发生一些问题，我们可以观察以下例子，为了演示方便，我将幂的底数设置大一些，设置为64。
在C语言中可以看到这样的结果：

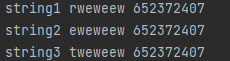
在python中可以见到这样的结果：

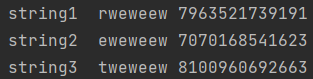
可见，不同语言会有不同的结果。原因在于python使用的是“长整型”，是以数组形式储存的，理论上拥有无限的长度[2]，而C语言中的整型是确定位数的储存，存在溢出的现象。
为了验证这种说法，我们可以对python得出的结果进行取余，取余的除数取决于c语言中的usigned int大小，这里是$2^{32}$。

可以看到取余的结果和C语言的结果完全一致，可以佐证溢出的结论。
至于为什么取余就是计算无符号整型溢出结果的方法，我也无法给出详细的证明，根据我看到的资料，这与溢出时抛弃最高位有关。
这就是取偶数的弊端，溢出时会导致一些哈希冲突，我们可以举几个例子。
按照偶数方法分别计算hash(rweweew), hash(eweweew), hash(tweweew)，64为2的6次方，我们将此替换64。

$hash(rweweew)=r\times 2^{42}+w\times 2^{36}+e\times 2^{30}+w\times 2^{24}+e\times 2^{18}+e\times 2^{12}+w\times 2^6$

$hash(eweweew)=e\times 2^{42}+w\times 2^{36}+e\times 2^{30}+w\times 2^{24}+e\times 2^{18}+e\times 2^{12}+w\times 2^6$

$hash(tweweew)=t\times 2^{42}+w\times 2^{36}+e\times 2^{30}+w\times 2^{24}+e\times 2^{18}+e\times 2^{12}+w\times 2^6$

由于发生溢出，高位被舍弃，我们对结果求余，根据取余（取模，在正数时无区别）的规则

$(a+b)\%m=(a\%m+b\%m)\%m$
$(a?b)\%m=(a\%m?b\%m)\%m$

可知，
$hash(rweweew)\%2^{32}=(r\times 2^{42}\%2^{32}+w\times 2^{36}\%2^{32}+...+w\times 2^6\%2^{32})\%2^{32}$

$hash(eweweew)\%2^{32}=(e\times 2^{42}\%2^{32}+w\times 2^{36}\%2^{32}+...+w\times 2^6\%2^{32})\%2^{32}$

$hash(tweweew)\%2^{32}=(t\times 2^{42}\%2^{32}+w\times 2^{36}\%2^{32}+...+w\times 2^6\%2^{32})\%2^{32}$

观察公式可以发现，大于$2^{32}$的部分（即rw, ew, tw）求余变为零，剩余部分则因为字符串完全相同导致计算出来的值是相同的。因此，最终计算出相同的哈希值。
最大的问题是，采用这种方法，当字符串到达一定长度以后，整型便会溢出，字符串的一部分便“不再参与”哈希值的计算了，导致一直碰撞，查找效率会急剧下降。
上面是以2的幂为底数的偶数的例子，至于除此之外的偶数为什么不建议用，我也不知道（本文参考的资料在这个上面的证明是错的），查到的少数资料基本上就没有用偶数的。如果读者有证明，可以提供一下。
一般来说，推荐使用奇数，而且建议为$2^n?1$之类的，据说因为cpu移位运算会快一些。
以上是bkdrhash的原理详解，以下结合实现进一步进行讲解。

bkdrhash的C语言实现

需要实现bkdrhash的查询，首先需要实现hash生成函数，也就是将上文介绍的原理转变为代码，这个相对来说比较简单。

unsigned int StrOriginHash(const char* string, unsigned int divisor)
{
    unsigned int hash = 0;
    int count = 0;
    // seed = 2^4 - 1 = 15
    int seed = 15;
    while(*string != '\0')
    {
        hash = hash * seed + *string;
        string++; // 指针移动到下一个字符
        if (++count >= hash_max_string_len)break; // hash_max_string_len = 10
        // 当字符串长度大于最大读取值时，自动忽略后续值
    }
    return hash%divisor; // 对hash取模，方便存入数组
}

通过这个函数，我们生成了一个hash，由于生成的hash一般非常大，我们需要将它对它取一个模，再对应数组的下标。
这个模的除数一般为一个质数，有助于降低碰撞的概率，具体为什么我也不知道。
接下来我们需要构造一个数组，用来储存数据。我才用了链地址法，这个数组是一个头节点数组，储存着头节点。这里用到了我自己写的链表的程序，比较复杂，这里仅仅放出它的头文件内容，并稍微解释以下其结构。

//
// Created by xs on 2021/8/23.
//

#ifndef NEWPRJ_LINKED_LIST_H
#define NEWPRJ_LINKED_LIST_H

#include <string.h>
#include <stdio.h>
#include <stdlib.h>

// 定义名字数组大小
#define data_name_buffer 30

// 定义char数据数组大小
#define data_char_buffer 30

// 定义type_name大小
#define data_type_str_buffer 30

#define operation_success 1
#define operation_fail 0

// 定义数据类型
#define data_type_none 0
#define data_type_int 1
#define data_type_char 2
#define data_type_float 3
#define data_type_double 4
#define data_type_node 5
#define data_type_head 6

struct node_;

typedef struct head_
{
    struct node_ *first_node;
    char name[data_name_buffer];
    struct head_ *last_head;
    int len;
}head;

typedef struct node_
{
    struct node_ *next;
    struct node_ *next1;
    char name[data_name_buffer];
    int data_type;
    void *data;
    head *node_head;
    struct node_ *last_node;
}node;

void HeadInit(head *head_pointer);
head *CreateEmptyLinkedList();
int NodeInit(node *node_pointer);
int NodeSetData(node *node_pointer, int type, char const *data_str);
node *ListInsertNode(node *node_pointer, head *head_pointer);
int InsertExistedNode(node *target_node, head *target_head, node *source_node);
node *HeadIndexLinkedList(head *head_pointer, int index);
int NodeTypePrint(node *node_pointer, char *str);
void PrintNode(node *node_pointer);
void Traverse(head *head_pointer, node *node_pointer);
void HeadDelSingleList(head *head_pointer);
void NodeDelSingleList(node *node_pointer);
void NodeDelLinkedList(node *node_pointer, int depth);
int SetHeadName(head *head_pointer, char const *str);
int SetNodeName(node *node_pointer, char const *str);

#endif //NEWPRJ_LINKED_LIST_H

我所构建的（单向）链表包括两种结构体，分别是储存整个链表信息的头结构体，以及储存数据的链表节点。
头结构体包含几个主要的内容：

• 链表的第一个节点
• 链表的名称
• 链表包含元素的数量（即长度len）

链表节点包括几个主要内容：

• 链表节点的名字name
• 链表的下一个节点next
• 链表的种类data_type，再宏定义中具体定义
• 指向数据地址的void指针

head与node其它部分的定义（next1等），在这里使用不上，就不再介绍了，读者可以忽略。数据地址采用了void类型主要为了通用性，通过data_type确定数据类型后，便可以确定指针指向数据的读取方式。这样子可以很方便的扩展容纳的数据类型，也可做到链表的嵌套。
如果读者需要实现bkdrhash，需要自己去实现链表，或者等待我将完整的学生成绩管理系统写完，放出源码。
对于链表的构建处理完成后，就是需要去构建哈希表，插入函数以及查找了。

// 构建哈希表结构体
// 包含哈希表和哈希表长度
// 方便查询
typedef struct
{
    head *hash_table;
    unsigned int hash_len;
}hash_table_struct;

// 建立哈希表
// 意味着需要建立哈希表的程序去维护
head *HashTableCreate(unsigned int divisor)
{
    head *hash_table;
    hash_table = (head*) malloc(sizeof(head)*divisor); // 开辟head数组，即哈希表
    hash_struct->hash_len = divisor; // 确定哈希表长度
    return hash_table; // 返回该哈希表
}

// 向哈希表中插入数据
// 处理字符串
int StrHashListInsertData(node *node_pointer, hash_table_struct *hash_struct)
{
    // operation_success = 1
    // operation_fail = 0
    unsigned int data_hash;
    node *index_node; // 用于寻找到对应节点
    node *temp_node; //临时节点，用于挂载在哈希表对应链表末尾
    // 非字符串类型，返回错误
    if (node_pointer->data_type != data_type_char)return operation_fail;
    data_hash = StrOriginHash(node_pointer->data, hash_struct->hash_len); // 计算字符串哈希值
    index_node = (hash_struct->hash_table[data_hash]).first_node;
    temp_node = (node*) malloc(sizeof(node));
    NodeInit(temp_node);
    // 以下两行与索引的架构有关
    temp_node->data_type = data_type_node;
    temp_node->data = node_pointer;
    if (index_node == NULL)
    {
        hash_struct->hash_table[data_hash].first_node = temp_node;
    }
    else
    {
        while(index_node->next != NULL)index_node = index_node->next; // 寻找到哈希表链表末尾
        index_node->next = temp_node; // 将temp节点挂载到链表末尾
    }
    return operation_success;
}

这里面需要专门解释一下几行代码，方便读者理解。

index_node = (hash_struct->hash_table[data_hash]).first_node;
index_node在这样子设置以后，即指向head后的第一个节点。
另外两行代码主要针对的我存储数据的结构设计的。

temp_node->data_type = data_type_node;
temp_node->data = node_pointer;

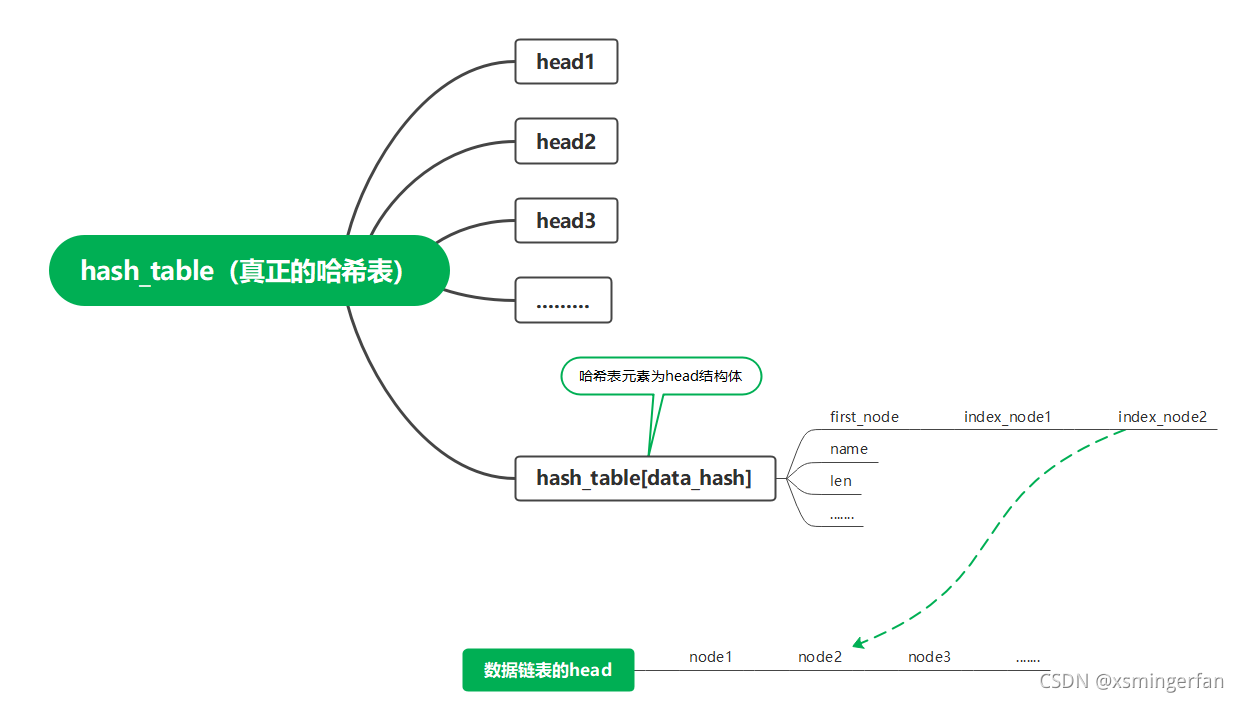
在我的学生成绩管理系统中，数据是单独储存的，由一个链表构成。哈希表仅仅是一个索引，因此哈希表的链表是不储存数据的。正如图中所示，哈希冲突后的链表节点被标注为index_node，它最终指向的是数据链表的节点。
在函数StrHashListInsertData(node *node_pointer, hash_table_struct *hash_struct)中，node_pointer即是传入的数据节点，而temp_node->data = node_pointer;就是将数据节点与哈希表的链表节点连接起来。这样一来，temp_node->data_type = data_type_node;也可以理解了。
完成节点的插入后，接下来就是完成哈希表的查询了。

// 哈希表查询
// 返回相应的数据节点
node *StrHashFind(const char *match_str, hash_table_struct *input_hash_table)
{
    unsigned int match_str_hash;
    node *temp_node; // 临时节点指针，用于遍历哈希表链表
    match_str_hash = StrOriginHash(match_str, input_hash_table->hash_len); // 产生匹配字符的哈希值
    temp_node = input_hash_table->hash_table[match_str_hash].first_node; // 找到哈希表链表第一个节点
    if (temp_node == NULL)return NULL;
    // 循环直到找到匹配项
    while(temp_node != NULL)
    {
        // 哈希表链表中节点映射的数据与搜索的字符串对比
        if (strcmp(((node*)temp_node->data)->data, match_str) == 0)return temp_node->data;
        temp_node = temp_node->next;
    }
    return NULL;
}

这里代码注释比较清晰，就不详细解释了。
做完这一步，其实还有一个比较重要的函数，就是删除哈希表及其链表的函数。由于是C语言且使用了malloc函数，需要去手动释放内存，否则会造成内存泄漏。

// 删除哈希表
int DelHashTable(hash_table_struct *input_hash_table)
{
    unsigned int count; // 用于索引哈希表内容并删除
    node *temp_node;
    if (input_hash_table == NULL)return operation_fail;
    // 遍历哈希表
    for (count = 0; count < input_hash_table->hash_len; count++)
    {
        temp_node = input_hash_table->hash_table[count].first_node;
        if (temp_node != NULL) // 哈希表在此处非空
        {
            // NodeDelSingleList()
            // 删除节点后接的那一条链
            // 传入节点地址
            // flag为0不包括节点自身，为1包括节点自身
            NodeDelSingleList(temp_node, 1);    // 删除哈希表链表
        }
    }
    free(input_hash_table); // 释放哈希表内存
    return operation_success;
}

这里要注意的是，释放哈希表的内存，不可以仅仅释放掉数组的内存，也要释放数组对应链表的内存，否则就不能算作完全释放哈希表的内存。另外，写程序时需要注意不要释放掉数据链表的内存，否则会造成严重的问题。

写完哈希表后，就是验证的工作了。

#include <stdio.h>
#include "linked_list.h"
#include "data_manager.h"
#include "HashManager.h"
#include <string.h>
#include <windows.h>

node *DataNode(node* input_node)
{
    if (input_node->data_type != data_type_node)return NULL;
    else return input_node->data;
}

int main()
{
    node *node_pointer;
    head *head_pointer;
    char input_string[50];  // 容纳输入的指令
    int running = 1; // 确定循环是否进行
    DWORD time; // 用于计时
    hash_table_struct *hash_student_number;
    head_pointer = ReadFileData("../student");  // 读取文件
    node_pointer = head_pointer->first_node;

    time = GetTickCount();
    //添加哈希表
    hash_student_number = DataAddHashTable(proper_divisor1, item_name_list[0], head_pointer);
    printf("Time: %lu ms\n", GetTickCount()-time);

    // 列举部分哈希表内容用于确认数据已读入
    for (unsigned int count = 0; count < hash_student_number->hash_len/100; count++)
    {
        Traverse(&(hash_student_number->hash_table[count]), NULL, DataNode);
    }

    while (running)
    {
        printf("Please type order:");
        scanf_s("%s", input_string, 50);
        if (strcmp(input_string, "EXIT") == 0)running = 0;  // 输入EXIT中止程序
        else if (strcmp(input_string, "FIND") == 0)
        {
            printf("Please type data you need find:");
            scanf_s("%s", input_string, 50);
            time = GetTickCount();
            PrintNode(StrHashFind(input_string, hash_student_number));
            printf("Time: %lu ms\n", GetTickCount()-time);
        }
    }
}

这里采用了哈希函数进行数据查询的方式，总共10万个数据得到的部分结果如下

Time: 46 ms
Please type order:FIND
Please type data you need find:19660654092
19660654092
Time: 0 ms

这里可以看到，构建哈希表使用了46ms，而查询使用了1ms不到的时间，作为对比，我附上普通查询的代码与时间。

node *FindData(head *data_pointer, char *data_name)
{
    node *temp_node, *temp_node1; // 用于遍历链表
    if (data_pointer == NULL || data_pointer->first_node == NULL)return NULL;
    temp_node = data_pointer->first_node;
    while (temp_node != NULL)
    {
        if (temp_node->data_type == data_type_head)
        {
            temp_node1 = ((head*)temp_node->data)->first_node;
            while (temp_node1 != NULL)
            {
                if (strcmp(temp_node1->name, data_name) == 0)
                {
                    return temp_node1;
                }
                temp_node1 = temp_node1->next;
            }
        }
        temp_node = temp_node->next;
    }
    return NULL;
}

Please type data you need find:19870387192
19870387192
Time: 16 ms

Please type data you need find:19470185124
19470185124
Time: 0 ms

Please type data you need find:19340284003
19340284003
Time: 31 ms

Please type data you need find:19520137066
19520137066
Time: 0 ms

Please type data you need find:19850927034
19850927034
Time: 15 ms

可以发现，时间在0ms至32ms不等。为了保证严谨性，我对相同数值尝试使用hash寻找，得到以下结果：

Please type data you need find:19870387192
19870387192
Time: 0 ms

Please type data you need find:19470185124
19470185124
Time: 0 ms

Please type data you need find:19340284003
19340284003
Time: 0 ms

Please type data you need find:19520137066
19520137066
Time: 0 ms

Please type data you need find:19850927034
19850927034
Time: 0 ms

以上结果全部小于1ms，因此可以很好的看出哈希算法的优越性，大大缩减了查找时间。
以上就是我关于bkdrhash的见解与实践。写这篇博文主要是为了让自己能够更好地理解这个算法。如果可以在加深自己对这个算法理解地同时，让阅读这篇文章的人可以了解如何使用这个算法，我会非常高兴。当然，这篇文章一定存在一些漏洞以及错误，希望读者能够予以指出。