以下内容来源互联网与书籍。
文章目录
1.决策树算法原理
决策树的基本原理是:对于一个数据集 D D D,其基本的格式是由多个未知关联的多个特征共同决定一个输出。如果是分类问题,那么最后的输出是类别;而如果是回归问题,最后输出的是一个回归值。而在决策树的思想中,就是要对多个未知关联的特征挑选出最合适的一个特征(比如使用信息增益等等),来对数据集 D D D进行划分,划分为多个子数据集。然后,对于这些同样的感觉信息增益进一步划分子数据集,这是一个迭代的过程,最后得到一整个的决策树结构来解决当前特征输出哪一类或者是输出哪一个特征值。
1.1 信息增益
一条信息的信息量和其不确定性有直接的关系。一个问题的不确定性越大,那么要搞清楚这个问题,需要了解的信息就越多,其信息熵就越大。信息熵的计算公式为:
H
(
X
)
=
?
∑
x
∈
X
P
(
x
)
log
?
2
P
(
x
)
H(X) = -\sum_{x \in X}P(x)\log_{2}P(x)
H(X)=?x∈X∑?P(x)log2?P(x)
其中:
P
(
x
)
P(x)
P(x)表示事件x出现的概率
而当构建一个决策树时,我们需要遍历所有的特征,如果选择特征前后信息熵的变化幅度最大的那一个特征 A A A,来优选作为数据集划分的依据。其中,这里涉及到的信息熵变化幅度也就是信息增益。其表示是划分数据前与根据特征 A A A划分数据后,数据集的信息熵的变化幅度。将信息增益定义为: g ( D , A ) g(D,A) g(D,A)
表达式为:
g
(
D
,
A
)
=
H
(
D
)
?
H
(
D
∣
A
)
g(D,A) = H(D)-H(D|A)
g(D,A)=H(D)?H(D∣A)
其中:
H
(
D
)
H(D)
H(D)表示经验熵,也就是数据集D本身的不确定性;而
H
(
D
∣
A
)
H(D|A)
H(D∣A)表示条件熵,是在A条件下集合D的不确定性。
而信息增益比可以表示为:
g
R
(
D
,
A
)
=
g
(
D
,
A
)
H
(
D
∣
A
)
g_{R}(D,A) = \frac{g(D,A)}{H(D|A)}
gR?(D,A)=H(D∣A)g(D,A)?
这里,我理解的是信息增益与训练集D关于特征A的信息熵。
1.1.1 信息增益计算例子
下面以一个例子说明具体的计算方法,比如一个盒子中有红白黑蓝4中颜色的球共16个。其中红球2个,白球2个,黑球4个,蓝球8个。其中红球黑球体积单位为1,而白球蓝球体积单位为2。红球白球黑球质量单位为1,而蓝球质量单位为2。
在决策树的思想里,我们要对这些球做一个分类,来更好预测。分类就需要挑选一个特征对数据集进行划分,而选择的特征有颜色,质量,体积,我们需要对这些特征分别计算其信息增益,来选择使得数据集更加有序。
- 首先,计算基础的信息熵
也就是划分数据集前的信息熵。红白黑蓝球出现的概率分别是:2/16、2/16、4/16、8/16。所以,划分前的信息熵计算为:
H
(
D
b
a
s
e
)
=
?
(
2
16
log
?
2
2
16
+
2
16
log
?
2
2
16
+
4
16
log
?
2
4
16
+
8
16
log
?
2
8
16
)
=
1.75
H(D_{base}) = -(\frac{2}{16}\log_{2}\frac{2}{16}+\frac{2}{16}\log_{2}\frac{2}{16}+\frac{4}{16}\log_{2}\frac{4}{16}+\frac{8}{16}\log_{2}\frac{8}{16})=1.75
H(Dbase?)=?(162?log2?162?+162?log2?162?+164?log2?164?+168?log2?168?)=1.75
- 计算体积特征的信息增益
现在选择体积这个特征对数据集进行划分,这时就会划分出两个数据集。因为红球黑球的体积单位是1,而白球蓝球的体积单位是2。对于第一个子数据集,红球黑球分别是2个与4个,概率分别为
2
6
\frac{2}{6}
62?、
4
6
\frac{4}{6}
64?,所以其信息熵为:
H
(
D
1
s
u
b
1
)
=
?
(
2
6
log
?
2
2
6
+
4
6
log
?
2
4
6
)
=
0.918296
H(D1_{sub1}) = -(\frac{2}{6}\log_{2}\frac{2}{6}+\frac{4}{6}\log_{2}\frac{4}{6})=0.918296
H(D1sub1?)=?(62?log2?62?+64?log2?64?)=0.918296
对于第二字数据集白球黑球分别是2个与8个,其概率分别为
2
10
\frac{2}{10}
102?、
8
10
\frac{8}{10}
108?,所以其信息熵为:
H
(
D
1
s
u
b
2
)
=
?
(
2
10
log
?
2
2
10
+
8
10
log
?
2
8
10
)
=
0.721928
H(D1_{sub2}) = -(\frac{2}{10}\log_{2}\frac{2}{10}+\frac{8}{10}\log_{2}\frac{8}{10})=0.721928
H(D1sub2?)=?(102?log2?102?+108?log2?108?)=0.721928
所以,使用了体积这个特征划分数据集后,其信息熵为:
H
(
D
1
)
=
H
(
D
1
s
u
b
1
)
+
H
(
D
1
s
u
b
2
)
H(D1) = H(D1_{sub1}) +H(D1_{sub2})
H(D1)=H(D1sub1?)+H(D1sub2?),其信息增益既为:
H
(
D
b
a
s
e
)
?
H
(
D
1
)
=
1.75
?
1.640224
=
0.109776
H(D_{base}) - H(D1) = 1.75-1.640224=0.109776
H(Dbase?)?H(D1)=1.75?1.640224=0.109776
- 计算质量特征的信息增益
同样的,对于质量这个特征同样可以对数据进行划分成两个子数据集,红白黑球的质量都是1个单位;而蓝球的质量单位是2。针对第一个子数据集,红白黑球出现的概率分别是2/8、2/8/、4/8,所以其信息熵为:
H
(
D
2
s
u
b
1
)
=
?
(
2
8
log
?
2
2
8
+
2
8
log
?
2
2
8
+
4
8
log
?
2
4
8
)
=
1.5
H(D2_{sub1}) = -(\frac{2}{8}\log_{2}\frac{2}{8}+\frac{2}{8}\log_{2}\frac{2}{8} +\frac{4}{8}\log_{2}\frac{4}{8})=1.5
H(D2sub1?)=?(82?log2?82?+82?log2?82?+84?log2?84?)=1.5
而第二个子数据集中只有蓝球,其概率为1,所以其信息熵为0。所以用质量划分的信息增益为:
H
(
D
b
a
s
e
)
?
H
(
D
2
)
=
1.75
?
1.5
=
0.25
H(D_{base}) - H(D2) = 1.75-1.5=0.25
H(Dbase?)?H(D2)=1.75?1.5=0.25
- 选择最高的信息增益
由于使用质量划分数据集比使用体积划分数据集得到了更高的信息增益,所以优先选择质量这个特征划分数据集。
1.1.2 信息增益代码实现
- 创建数据集,计算经验熵的代码如下:
from math import log
"""
函数说明:创建测试数据集
Parameters:无
Returns:
dataSet:数据集
labels:分类属性
Modify:
2018-03-12
"""
def creatDataSet():
# 数据集
dataSet=[[0, 0, 0, 0, 'no'],
[0, 0, 0, 1, 'no'],
[0, 1, 0, 1, 'yes'],
[0, 1, 1, 0, 'yes'],
[0, 0, 0, 0, 'no'],
[1, 0, 0, 0, 'no'],
[1, 0, 0, 1, 'no'],
[1, 1, 1, 1, 'yes'],
[1, 0, 1, 2, 'yes'],
[1, 0, 1, 2, 'yes'],
[2, 0, 1, 2, 'yes'],
[2, 0, 1, 1, 'yes'],
[2, 1, 0, 1, 'yes'],
[2, 1, 0, 2, 'yes'],
[2, 0, 0, 0, 'no']]
#分类属性
labels=['年龄','有工作','有自己的房子','信贷情况']
#返回数据集和分类属性
return dataSet,labels
"""
函数说明:计算给定数据集的经验熵(香农熵)
Parameters:
dataSet:数据集
Returns:
shannonEnt:经验熵
Modify:
2018-03-12
"""
def calcShannonEnt(dataSet):
#返回数据集行数
numEntries=len(dataSet)
#保存每个标签(label)出现次数的字典
labelCounts={}
#对每组特征向量进行统计
for featVec in dataSet:
currentLabel=featVec[-1] #提取标签信息
if currentLabel not in labelCounts.keys(): #如果标签没有放入统计次数的字典,添加进去
labelCounts[currentLabel]=0
labelCounts[currentLabel]+=1 #label计数
shannonEnt=0.0 #经验熵
#计算经验熵
for key in labelCounts:
prob=float(labelCounts[key])/numEntries #选择该标签的概率
shannonEnt-=prob*log(prob,2) #利用公式计算
return shannonEnt #返回经验熵
#main函数
if __name__=='__main__':
dataSet,features=creatDataSet()
print(dataSet)
print(calcShannonEnt(dataSet))
结果:
第0个特征的增益为0.083
第1个特征的增益为0.324
第2个特征的增益为0.420
第3个特征的增益为0.363
第0个特征的增益为0.252
第1个特征的增益为0.918
第2个特征的增益为0.474
{'有自己的房子': {0: {'有工作': {0: 'no', 1: 'yes'}}, 1: 'yes'}}
- 利用代码计算信息增益
from math import log
"""
函数说明:创建测试数据集
Parameters:无
Returns:
dataSet:数据集
labels:分类属性
Modify:
2018-03-12
"""
def creatDataSet():
# 数据集
dataSet=[[0, 0, 0, 0, 'no'],
[0, 0, 0, 1, 'no'],
[0, 1, 0, 1, 'yes'],
[0, 1, 1, 0, 'yes'],
[0, 0, 0, 0, 'no'],
[1, 0, 0, 0, 'no'],
[1, 0, 0, 1, 'no'],
[1, 1, 1, 1, 'yes'],
[1, 0, 1, 2, 'yes'],
[1, 0, 1, 2, 'yes'],
[2, 0, 1, 2, 'yes'],
[2, 0, 1, 1, 'yes'],
[2, 1, 0, 1, 'yes'],
[2, 1, 0, 2, 'yes'],
[2, 0, 0, 0, 'no']]
#分类属性
labels=['年龄','有工作','有自己的房子','信贷情况']
#返回数据集和分类属性
return dataSet,labels
"""
函数说明:计算给定数据集的经验熵(香农熵)
Parameters:
dataSet:数据集
Returns:
shannonEnt:经验熵
Modify:
2018-03-12
"""
def calcShannonEnt(dataSet):
#返回数据集行数
numEntries=len(dataSet)
#保存每个标签(label)出现次数的字典
labelCounts={}
#对每组特征向量进行统计
for featVec in dataSet:
currentLabel=featVec[-1] #提取标签信息
if currentLabel not in labelCounts.keys(): #如果标签没有放入统计次数的字典,添加进去
labelCounts[currentLabel]=0
labelCounts[currentLabel]+=1 #label计数
shannonEnt=0.0 #经验熵
#计算经验熵
for key in labelCounts:
prob=float(labelCounts[key])/numEntries #选择该标签的概率
shannonEnt-=prob*log(prob,2) #利用公式计算
return shannonEnt #返回经验熵
"""
函数说明:计算给定数据集的经验熵(香农熵)
Parameters:
dataSet:数据集
Returns:
shannonEnt:信息增益最大特征的索引值
Modify:
2018-03-12
"""
def chooseBestFeatureToSplit(dataSet):
#特征数量
numFeatures = len(dataSet[0]) - 1
#计数数据集的香农熵
baseEntropy = calcShannonEnt(dataSet)
#信息增益
bestInfoGain = 0.0
#最优特征的索引值
bestFeature = -1
#遍历所有特征
for i in range(numFeatures):
# 获取dataSet的第i个所有特征
featList = [example[i] for example in dataSet]
#创建set集合{},元素不可重复
uniqueVals = set(featList)
#经验条件熵
newEntropy = 0.0
#计算信息增益
for value in uniqueVals:
#subDataSet划分后的子集
subDataSet = splitDataSet(dataSet, i, value)
#计算子集的概率
prob = len(subDataSet) / float(len(dataSet))
#根据公式计算经验条件熵
newEntropy += prob * calcShannonEnt((subDataSet))
#信息增益
infoGain = baseEntropy - newEntropy
#打印每个特征的信息增益
print("第%d个特征的增益为%.3f" % (i, infoGain))
#计算信息增益
if (infoGain > bestInfoGain):
#更新信息增益,找到最大的信息增益
bestInfoGain = infoGain
#记录信息增益最大的特征的索引值
bestFeature = i
#返回信息增益最大特征的索引值
return bestFeature
"""
函数说明:按照给定特征划分数据集
Parameters:
dataSet:待划分的数据集
axis:划分数据集的特征
value:需要返回的特征的值
Returns:
shannonEnt:经验熵
Modify:
2018-03-12
"""
def splitDataSet(dataSet,axis,value):
retDataSet=[]
for featVec in dataSet:
if featVec[axis]==value:
reducedFeatVec=featVec[:axis]
reducedFeatVec.extend(featVec[axis+1:])
retDataSet.append(reducedFeatVec)
return retDataSet
#main函数
if __name__=='__main__':
dataSet,features=creatDataSet()
# print(dataSet)
# print(calcShannonEnt(dataSet))
print("最优索引值:"+str(chooseBestFeatureToSplit(dataSet)))
结果:
第0个特征的增益为0.083
第1个特征的增益为0.324
第2个特征的增益为0.420
第3个特征的增益为0.363
最优索引值:2
1.2 决策树的构建
决策树的创建基本上分为以下几步:
1)计算数据集划分前的信息熵
2)遍历所以未作为划分条件的特征,分别计算根据每个特征划分数据集后的信息熵
3)选择想你想增益最大的特征,并使用这个特征作为数据划分节点来划分数据
4)递归处理被划分后的所以子数据集,从未被选择的特征里继续选择最优数据划分特征来划分子数据集
其中:递归结束的终止条件有两个:
一是所以的特征都用完了,没有新的特征可以用来进一步划分数据集。
二是划分后的信息增益足够小了。
在后面的内容会提及到,sklearn中提供了许多的参数来选择数据集的样本大小后者是决策树的叶子节点的大小又或者是决策树的深度等等。不过这里首先是用代码直观了解,而不是简单调用。
其中,使用信息增益作为特征选择指标的决策树构建算法称为ID3算法;而使用信息增益比作为特征选择指标的决策树构建算法称为C4.5算法
1.2.1 ID3、C4.5、CART算法
这三个是非常著名的决策树算法。简单粗暴来说,ID3 使用信息增益作为选择特征的准则;C4.5 使用信息增益比作为选择特征的准则;CART 使用 Gini 指数作为选择特征的准则。
- ID3算法
熵表示的是数据中包含的信息量大小。熵越小,数据的纯度越高,也就是说数据越趋于一致,这是我们希望的划分之后每个子节点的样子。
信息增益 = 划分前熵 - 划分后熵。信息增益越大,则意味着使用属性 a 来进行划分所获得的 “纯度提升” 越大 **。也就是说,用属性 a 来划分训练集,得到的结果中纯度比较高。
ID3 仅仅适用于二分类问题。ID3 仅仅能够处理离散属性。
- C4.5算法
C4.5 克服了 ID3 仅仅能够处理离散属性的问题,以及信息增益偏向选择取值较多特征的问题,使用信息增益比来选择特征。信息增益比 = 信息增益 / 划分前熵 选择信息增益比最大的作为最优特征。
C4.5 处理连续特征是先将特征取值排序,以连续两个值中间值作为划分标准。尝试每一种划分,并计算修正后的信息增益,选择信息增益最大的分裂点作为该属性的分裂点。
- CART算法
CART 与 ID3,C4.5 不同之处在于 CART 生成的树必须是二叉树。也就是说,无论是回归还是分类问题,无论特征是离散的还是连续的,无论属性取值有多个还是两个,内部节点只能根据属性值进行二分。
CART 的全称是分类与回归树。从这个名字中就应该知道,CART 既可以用于分类问题,也可以用于回归问题。
回归树中,使用平方误差最小化准则来选择特征并进行划分。每一个叶子节点给出的预测值,是划分到该叶子节点的所有样本目标值的均值,这样只是在给定划分的情况下最小化了平方误差。
要确定最优化分,还需要遍历所有属性,以及其所有的取值来分别尝试划分并计算在此种划分情况下的最小平方误差,选取最小的作为此次划分的依据。由于回归树生成使用平方误差最小化准则,所以又叫做最小二乘回归树。
分类树种,使用 Gini 指数最小化准则来选择特征并进行划分;
Gini 指数表示集合的不确定性,或者是不纯度。基尼指数越大,集合不确定性越高,不纯度也越大。这一点和熵类似。另一种理解基尼指数的思路是,基尼指数是为了最小化误分类的概率。
信息增益 vs 信息增益比
之所以引入了信息增益比,是由于信息增益的一个缺点。那就是:信息增益总是偏向于选择取值较多的属性。信息增益比在此基础上增加了一个罚项,解决了这个问题。
Gini 指数 vs 熵
既然这两个都可以表示数据的不确定性,不纯度。那么这两个有什么区别那?
- Gini 指数的计算不需要对数运算,更加高效;
- Gini 指数更偏向于连续属性,熵更偏向于离散属性。
1.2.2 ID3算法代码实现
编写ID3算法的代码
from math import log
import operator
"""
函数说明:计算给定数据集的经验熵(香农熵)
Parameters:
dataSet:数据集
Returns:
shannonEnt:经验熵
Modify:
2018-03-12
"""
def calcShannonEnt(dataSet):
#返回数据集行数
numEntries=len(dataSet)
#保存每个标签(label)出现次数的字典
labelCounts={}
#对每组特征向量进行统计
for featVec in dataSet:
currentLabel=featVec[-1] #提取标签信息
if currentLabel not in labelCounts.keys(): #如果标签没有放入统计次数的字典,添加进去
labelCounts[currentLabel]=0
labelCounts[currentLabel]+=1 #label计数
shannonEnt=0.0 #经验熵
#计算经验熵
for key in labelCounts:
prob=float(labelCounts[key])/numEntries #选择该标签的概率
shannonEnt-=prob*log(prob,2) #利用公式计算
return shannonEnt #返回经验熵
"""
函数说明:创建测试数据集
Parameters:无
Returns:
dataSet:数据集
labels:分类属性
Modify:
2018-03-13
"""
def createDataSet():
# 数据集
dataSet=[[0, 0, 0, 0, 'no'],
[0, 0, 0, 1, 'no'],
[0, 1, 0, 1, 'yes'],
[0, 1, 1, 0, 'yes'],
[0, 0, 0, 0, 'no'],
[1, 0, 0, 0, 'no'],
[1, 0, 0, 1, 'no'],
[1, 1, 1, 1, 'yes'],
[1, 0, 1, 2, 'yes'],
[1, 0, 1, 2, 'yes'],
[2, 0, 1, 2, 'yes'],
[2, 0, 1, 1, 'yes'],
[2, 1, 0, 1, 'yes'],
[2, 1, 0, 2, 'yes'],
[2, 0, 0, 0, 'no']]
#分类属性
labels=['年龄','有工作','有自己的房子','信贷情况']
#返回数据集和分类属性
return dataSet,labels
"""
函数说明:按照给定特征划分数据集
Parameters:
dataSet:待划分的数据集
axis:划分数据集的特征
value:需要返回的特征值
Returns:
无
Modify:
2018-03-13
"""
def splitDataSet(dataSet,axis,value):
#创建返回的数据集列表
retDataSet=[]
#遍历数据集
for featVec in dataSet:
if featVec[axis]==value:
#去掉axis特征
reduceFeatVec=featVec[:axis]
#将符合条件的添加到返回的数据集
reduceFeatVec.extend(featVec[axis+1:])
retDataSet.append(reduceFeatVec)
#返回划分后的数据集
return retDataSet
"""
函数说明:计算给定数据集的经验熵(香农熵)
Parameters:
dataSet:数据集
Returns:
shannonEnt:信息增益最大特征的索引值
Modify:
2018-03-13
"""
def chooseBestFeatureToSplit(dataSet):
#特征数量
numFeatures = len(dataSet[0]) - 1
#计数数据集的香农熵
baseEntropy = calcShannonEnt(dataSet)
#信息增益
bestInfoGain = 0.0
#最优特征的索引值
bestFeature = -1
#遍历所有特征
for i in range(numFeatures):
# 获取dataSet的第i个所有特征
featList = [example[i] for example in dataSet]
#创建set集合{},元素不可重复
uniqueVals = set(featList)
#经验条件熵
newEntropy = 0.0
#计算信息增益
for value in uniqueVals:
#subDataSet划分后的子集
subDataSet = splitDataSet(dataSet, i, value)
#计算子集的概率
prob = len(subDataSet) / float(len(dataSet))
#根据公式计算经验条件熵
newEntropy += prob * calcShannonEnt((subDataSet))
#信息增益
infoGain = baseEntropy - newEntropy
#打印每个特征的信息增益
print("第%d个特征的增益为%.3f" % (i, infoGain))
#计算信息增益
if (infoGain > bestInfoGain):
#更新信息增益,找到最大的信息增益
bestInfoGain = infoGain
#记录信息增益最大的特征的索引值
bestFeature = i
#返回信息增益最大特征的索引值
return bestFeature
"""
函数说明:统计classList中出现次数最多的元素(类标签)
Parameters:
classList:类标签列表
Returns:
sortedClassCount[0][0]:出现次数最多的元素(类标签)
Modify:
2018-03-13
"""
def majorityCnt(classList):
classCount={}
#统计classList中每个元素出现的次数
for vote in classList:
if vote not in classCount.keys():
classCount[vote]=0
classCount[vote]+=1
#根据字典的值降序排列
sortedClassCount=sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)
return sortedClassCount[0][0]
"""
函数说明:创建决策树
Parameters:
dataSet:训练数据集
labels:分类属性标签
featLabels:存储选择的最优特征标签
Returns:
myTree:决策树
Modify:
2018-03-13
"""
def createTree(dataSet,labels,featLabels):
#取分类标签(是否放贷:yes or no)
classList=[example[-1] for example in dataSet]
#如果类别完全相同,则停止继续划分
if classList.count(classList[0])==len(classList):
return classList[0]
#遍历完所有特征时返回出现次数最多的类标签
if len(dataSet[0])==1:
return majorityCnt(classList)
#选择最优特征
bestFeat=chooseBestFeatureToSplit(dataSet)
#最优特征的标签
bestFeatLabel=labels[bestFeat]
featLabels.append(bestFeatLabel)
#根据最优特征的标签生成树
myTree={bestFeatLabel:{}}
#删除已经使用的特征标签
del(labels[bestFeat])
#得到训练集中所有最优特征的属性值
featValues=[example[bestFeat] for example in dataSet]
#去掉重复的属性值
uniqueVls=set(featValues)
#遍历特征,创建决策树
for value in uniqueVls:
myTree[bestFeatLabel][value]=createTree(splitDataSet(dataSet,bestFeat,value),
labels,featLabels)
return myTree
if __name__=='__main__':
dataSet,labels=createDataSet()
featLabels=[]
myTree=createTree(dataSet,labels,featLabels)
print(myTree)
结果:
第0个特征的增益为0.083
第1个特征的增益为0.324
第2个特征的增益为0.420
第3个特征的增益为0.363
第0个特征的增益为0.252
第1个特征的增益为0.918
第2个特征的增益为0.474
{'有自己的房子': {0: {'有工作': {0: 'no', 1: 'yes'}}, 1: 'yes'}}
1.3 决策树剪枝处理
决策树生成算法递归的产生决策树,直到不能继续下去为止,这样产生的树往往对训练数据的分类很准确,但对未知测试数据的分类缺没有那么精确,即会出现过拟合现象。过拟合产生的原因在于在学习时过多的考虑如何提高对训练数据的正确分类,从而构建出过于复杂的决策树,解决方法是考虑决策树的复杂度,对已经生成的树进行简化。
1.3.1 前剪枝
前剪枝是在构造决策树的同时进行剪枝。
1)使用阈值进行限定
在决策树的构建过程中,信息熵已经无法进一步的降低,已经低过所设置的阈值,停止分支
2)限制叶子节点样本个数
当样本个数小于一定的阈值时,不再继续创建分支也可以进行剪枝
sklearn中提高了许多前剪枝的参数,可以自由设置,或者所以GridSearchCV进行寻找最优参数。
1.3.2 后剪枝
后剪枝是指决策树构造完成后进行剪枝处理。剪枝的过程是对拥有同样的父节点的一组节点进行检查,判断如果将其合并,信息熵的增加量是否小于某一个阈值。如果小于阈值,则这一组节点可以合并一个节点。
但是sklearn没有提供后剪枝的方法。
1.4 决策数分类实现
依靠训练数据构造了决策树之后,我们可以将它用于实际数据的分类。在执行数据分类时,需要决策树以及用于构造树的标签向量。然后,程序比较测试数据与决策树上的数值,递归执行该过程直到进入叶子结点;最后将测试数据定义为叶子结点所属的类型。在构建决策树的代码,可以看到,有个featLabels参数。它是用来干什么的?它就是用来记录各个分类结点的,在用决策树做预测的时候,我们按顺序输入需要的分类结点的属性值即可。举个例子,比如我用上述已经训练好的决策树做分类,那么我只需要提供这个人是否有房子,是否有工作这两个信息即可,无需提供冗余的信息。
代码如下:
from math import log
import operator
"""
函数说明:计算给定数据集的经验熵(香农熵)
Parameters:
dataSet:数据集
Returns:
shannonEnt:经验熵
Modify:
2018-03-12
"""
def calcShannonEnt(dataSet):
#返回数据集行数
numEntries=len(dataSet)
#保存每个标签(label)出现次数的字典
labelCounts={}
#对每组特征向量进行统计
for featVec in dataSet:
currentLabel=featVec[-1] #提取标签信息
if currentLabel not in labelCounts.keys(): #如果标签没有放入统计次数的字典,添加进去
labelCounts[currentLabel]=0
labelCounts[currentLabel]+=1 #label计数
shannonEnt=0.0 #经验熵
#计算经验熵
for key in labelCounts:
prob=float(labelCounts[key])/numEntries #选择该标签的概率
shannonEnt-=prob*log(prob,2) #利用公式计算
return shannonEnt #返回经验熵
"""
函数说明:创建测试数据集
Parameters:无
Returns:
dataSet:数据集
labels:分类属性
Modify:
2018-03-13
"""
def createDataSet():
# 数据集
dataSet=[[0, 0, 0, 0, 'no'],
[0, 0, 0, 1, 'no'],
[0, 1, 0, 1, 'yes'],
[0, 1, 1, 0, 'yes'],
[0, 0, 0, 0, 'no'],
[1, 0, 0, 0, 'no'],
[1, 0, 0, 1, 'no'],
[1, 1, 1, 1, 'yes'],
[1, 0, 1, 2, 'yes'],
[1, 0, 1, 2, 'yes'],
[2, 0, 1, 2, 'yes'],
[2, 0, 1, 1, 'yes'],
[2, 1, 0, 1, 'yes'],
[2, 1, 0, 2, 'yes'],
[2, 0, 0, 0, 'no']]
#分类属性
labels=['年龄','有工作','有自己的房子','信贷情况']
#返回数据集和分类属性
return dataSet,labels
"""
函数说明:按照给定特征划分数据集
Parameters:
dataSet:待划分的数据集
axis:划分数据集的特征
value:需要返回的特征值
Returns:
无
Modify:
2018-03-13
"""
def splitDataSet(dataSet,axis,value):
#创建返回的数据集列表
retDataSet=[]
#遍历数据集
for featVec in dataSet:
if featVec[axis]==value:
#去掉axis特征
reduceFeatVec=featVec[:axis]
#将符合条件的添加到返回的数据集
reduceFeatVec.extend(featVec[axis+1:])
retDataSet.append(reduceFeatVec)
#返回划分后的数据集
return retDataSet
"""
函数说明:计算给定数据集的经验熵(香农熵)
Parameters:
dataSet:数据集
Returns:
shannonEnt:信息增益最大特征的索引值
Modify:
2018-03-13
"""
def chooseBestFeatureToSplit(dataSet):
#特征数量
numFeatures = len(dataSet[0]) - 1
#计数数据集的香农熵
baseEntropy = calcShannonEnt(dataSet)
#信息增益
bestInfoGain = 0.0
#最优特征的索引值
bestFeature = -1
#遍历所有特征
for i in range(numFeatures):
# 获取dataSet的第i个所有特征
featList = [example[i] for example in dataSet]
#创建set集合{},元素不可重复
uniqueVals = set(featList)
#经验条件熵
newEntropy = 0.0
#计算信息增益
for value in uniqueVals:
#subDataSet划分后的子集
subDataSet = splitDataSet(dataSet, i, value)
#计算子集的概率
prob = len(subDataSet) / float(len(dataSet))
#根据公式计算经验条件熵
newEntropy += prob * calcShannonEnt((subDataSet))
#信息增益
infoGain = baseEntropy - newEntropy
#打印每个特征的信息增益
print("第%d个特征的增益为%.3f" % (i, infoGain))
#计算信息增益
if (infoGain > bestInfoGain):
#更新信息增益,找到最大的信息增益
bestInfoGain = infoGain
#记录信息增益最大的特征的索引值
bestFeature = i
#返回信息增益最大特征的索引值
return bestFeature
"""
函数说明:统计classList中出现次数最多的元素(类标签)
Parameters:
classList:类标签列表
Returns:
sortedClassCount[0][0]:出现次数最多的元素(类标签)
Modify:
2018-03-13
"""
def majorityCnt(classList):
classCount={}
#统计classList中每个元素出现的次数
for vote in classList:
if vote not in classCount.keys():
classCount[vote]=0
classCount[vote]+=1
#根据字典的值降序排列
sortedClassCount=sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)
return sortedClassCount[0][0]
"""
函数说明:创建决策树
Parameters:
dataSet:训练数据集
labels:分类属性标签
featLabels:存储选择的最优特征标签
Returns:
myTree:决策树
Modify:
2018-03-13
"""
def createTree(dataSet,labels,featLabels):
#取分类标签(是否放贷:yes or no)
classList=[example[-1] for example in dataSet]
#如果类别完全相同,则停止继续划分
if classList.count(classList[0])==len(classList):
return classList[0]
#遍历完所有特征时返回出现次数最多的类标签
if len(dataSet[0])==1:
return majorityCnt(classList)
#选择最优特征
bestFeat=chooseBestFeatureToSplit(dataSet)
#最优特征的标签
bestFeatLabel=labels[bestFeat]
featLabels.append(bestFeatLabel)
#根据最优特征的标签生成树
myTree={bestFeatLabel:{}}
#删除已经使用的特征标签
del(labels[bestFeat])
#得到训练集中所有最优特征的属性值
featValues=[example[bestFeat] for example in dataSet]
#去掉重复的属性值
uniqueVls=set(featValues)
#遍历特征,创建决策树
for value in uniqueVls:
myTree[bestFeatLabel][value]=createTree(splitDataSet(dataSet,bestFeat,value),
labels,featLabels)
return myTree
"""
使用决策树进行分类
Parameters:
inputTree;已经生成的决策树
featLabels:存储选择的最优特征标签
testVec:测试数据列表,顺序对应最优特征标签
Returns:
classLabel:分类结果
Modify:2018-03-13
"""
def classify(inputTree,featLabels,testVec):
#获取决策树节点
firstStr=next(iter(inputTree))
#下一个字典
secondDict=inputTree[firstStr]
featIndex=featLabels.index(firstStr)
for key in secondDict.keys():
if testVec[featIndex]==key:
if type(secondDict[key]).__name__=='dict':
classLabel=classify(secondDict[key],featLabels,testVec)
else: classLabel=secondDict[key]
return classLabel
if __name__=='__main__':
dataSet,labels=createDataSet()
featLabels=[]
myTree=createTree(dataSet,labels,featLabels)
#测试数据
testVec=[0,1]
result=classify(myTree,featLabels,testVec)
if result=='yes':
print('放贷')
if result=='no':
print('不放贷')
结果:
第0个特征的增益为0.083
第1个特征的增益为0.324
第2个特征的增益为0.420
第3个特征的增益为0.363
第0个特征的增益为0.252
第1个特征的增益为0.918
第2个特征的增益为0.474
放贷
1.5 决策树的加载与存储
1.5.1 决策树存储
构造决策树是很耗时的任务,即使处理很小的数据集,如前面的样本数据,也要花费几秒的时间,如果数据集很大,将会耗费很多计算时间。然而用创建好的决策树解决分类问题,则可以很快完成。因此,为了节省计算时间,最好能够在每次执行分类时调用已经构造好的决策树。为了解决这个问题,需要使用Python模块pickle序列化对象。序列化对象可以在磁盘上保存对象,并在需要的时候读取出来。
假设我们已经得到决策树
{'有自己的房子': {0: {'有工作': {0: 'no', 1: 'yes'}}, 1: 'yes'}}
使用pickle.dump存储决策树。
import pickle
"""
函数说明:存储决策树
Parameters:
inputTree:已经生成的决策树
filename:决策树的存储文件名
Returns:
无
Modify:
2018-03-13
"""
def storeTree(inputTree,filename):
with open(filename,'wb') as fw:
pickle.dump(inputTree,fw)
if __name__=='__main__':
myTree={'有自己的房子':{0:{'有工作':{0:'no',1:'yes'}},1:'yes'}}
storeTree(myTree,'classifierStorage.txt')
运行代码,在该Python文件的相同目录下,会生成一个名为classifierStorage.txt的txt文件,这个文件二进制存储着我们的决策树。
1.5.2 决策树的加载
很简单使用pickle.load进行载入即可,编写代码如下:
import pickle
"""
函数说明:读取决策树
Parameters:
filename:决策树的存储文件名
Returns:
pickle.load(fr):决策树字典
Modify:
2018-03-13
"""
def grabTree(filename):
fr = open(filename, 'rb')
return pickle.load(fr)
if __name__ == '__main__':
myTree = grabTree('classifierStorage.txt')
print(myTree)
通过以上的代码实现应该能比较清晰的了解决策树的具体过程。但是一般使用的时候直接调用sklearn实现的工具包即可,不可能自己从头可以写一个决策树算法去使用。所以,下面内容会介绍sklearn的决策树使用。
2. 决策树算法使用
在sklearn中sklearn.tree,提供了决策树使用的两个接口,分别用来解决分类问题与回归问题DecisionTreeClassifier,DecisionTreeRegressor
下面对DecisionTreeClassifier函数进行简单介绍:
class sklearn.tree.DecisionTreeClassifier(
criterion=’gini’,
splitter=’best’,
max_depth=None,
min_samples_split=2,
min_samples_leaf=1,
min_weight_fraction_leaf=0.0,
max_features=None,
random_state=None,
max_leaf_nodes=None,
min_impurity_decrease=0.0,
min_impurity_split=None,
class_weight=None,
presort=False)[source]
参数说明如下:
criterion:特征选择标准,可选参数,默认是gini,可以设置为entropy。gini是基尼不纯度,是将来自集合的某种结果随机应用于某一数据项的预期误差率,是一种基于统计的思想。entropy是香农熵,也就是上篇文章讲过的内容,是一种基于信息论的思想。Sklearn把gini设为默认参数,应该也是做了相应的斟酌的,精度也许更高些?ID3算法使用的是entropy,CART算法使用的则是gini。
splitter:特征划分点选择标准,可选参数,默认是best,可以设置为random。每个结点的选择策略。best参数是根据算法选择最佳的切分特征,例如gini、entropy。random随机的在部分划分点中找局部最优的划分点。默认的”best”适合样本量不大的时候,而如果样本数据量非常大,此时决策树构建推荐”random”。
max_features:划分时考虑的最大特征数,可选参数,默认是None。寻找最佳切分时考虑的最大特征数(n_features为总共的特征数),有如下6种情况:
如果max_features是整型的数,则考虑max_features个特征;
如果max_features是浮点型的数,则考虑int(max_features * n_features)个特征;
如果max_features设为auto,那么max_features = sqrt(n_features);
如果max_features设为sqrt,那么max_featrues = sqrt(n_features),跟auto一样;
如果max_features设为log2,那么max_features = log2(n_features);
如果max_features设为None,那么max_features = n_features,也就是所有特征都用。
一般来说,如果样本特征数不多,比如小于50,我们用默认的”None”就可以了,如果特征数非常多,我们可以灵活使用刚才描述的其他取值来控制划分时考虑的最大特征数,以控制决策树的生成时间。
max_depth:决策树最大深,可选参数,默认是None。这个参数是这是树的层数的。层数的概念就是,比如在贷款的例子中,决策树的层数是2层。如果这个参数设置为None,那么决策树在建立子树的时候不会限制子树的深度。一般来说,数据少或者特征少的时候可以不管这个值。或者如果设置了min_samples_slipt参数,那么直到少于min_smaples_split个样本为止。如果模型样本量多,特征也多的情况下,推荐限制这个最大深度,具体的取值取决于数据的分布。常用的可以取值10-100之间。
min_samples_split:内部节点再划分所需最小样本数,可选参数,默认是2。这个值限制了子树继续划分的条件。如果min_samples_split为整数,那么在切分内部结点的时候,min_samples_split作为最小的样本数,也就是说,如果样本已经少于min_samples_split个样本,则停止继续切分。如果min_samples_split为浮点数,那么min_samples_split就是一个百分比,ceil(min_samples_split * n_samples),数是向上取整的。如果样本量不大,不需要管这个值。如果样本量数量级非常大,则推荐增大这个值。
min_weight_fraction_leaf:叶子节点最小的样本权重和,可选参数,默认是0。这个值限制了叶子节点所有样本权重和的最小值,如果小于这个值,则会和兄弟节点一起被剪枝。一般来说,如果我们有较多样本有缺失值,或者分类树样本的分布类别偏差很大,就会引入样本权重,这时我们就要注意这个值了。
max_leaf_nodes:最大叶子节点数,可选参数,默认是None。通过限制最大叶子节点数,可以防止过拟合。如果加了限制,算法会建立在最大叶子节点数内最优的决策树。如果特征不多,可以不考虑这个值,但是如果特征分成多的话,可以加以限制,具体的值可以通过交叉验证得到。
class_weight:类别权重,可选参数,默认是None,也可以字典、字典列表、balanced。指定样本各类别的的权重,主要是为了防止训练集某些类别的样本过多,导致训练的决策树过于偏向这些类别。类别的权重可以通过{class_label:weight}这样的格式给出,这里可以自己指定各个样本的权重,或者用balanced,如果使用balanced,则算法会自己计算权重,样本量少的类别所对应的样本权重会高。当然,如果你的样本类别分布没有明显的偏倚,则可以不管这个参数,选择默认的None。
random_state:可选参数,默认是None。随机数种子。如果是证书,那么random_state会作为随机数生成器的随机数种子。随机数种子,如果没有设置随机数,随机出来的数与当前系统时间有关,每个时刻都是不同的。如果设置了随机数种子,那么相同随机数种子,不同时刻产生的随机数也是相同的。如果是RandomState instance,那么random_state是随机数生成器。如果为None,则随机数生成器使用np.random。
min_impurity_split:节点划分最小不纯度,可选参数,默认是1e-7。这是个阈值,这个值限制了决策树的增长,如果某节点的不纯度(基尼系数,信息增益,均方差,绝对差)小于这个阈值,则该节点不再生成子节点。即为叶子节点 。
presort:数据是否预排序,可选参数,默认为False,这个值是布尔值,默认是False不排序。一般来说,如果样本量少或者限制了一个深度很小的决策树,设置为true可以让划分点选择更加快,决策树建立的更加快。如果样本量太大的话,反而没有什么好处。问题是样本量少的时候,我速度本来就不慢。所以这个值一般懒得理它就可以了。
2.1 决策树解决分类问题
在解决分类问题中,这里以预测泰坦尼克号幸存者为示例介绍。决策树解决分类任务的基本思想是,将使用特征对数据集划分为多个样本类,然后对于需要预测的样本一一解析。
首先进行导入数据
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
data = pd.read_csv('train.csv')
data.head()
| PassengerId | Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 3 | Braund, Mr. Owen Harris | male | 22.0 | 1 | 0 | A/5 21171 | 7.2500 | NaN | S |
| 1 | 2 | 1 | 1 | Cumings, Mrs. John Bradley (Florence Briggs Th... | female | 38.0 | 1 | 0 | PC 17599 | 71.2833 | C85 | C |
| 2 | 3 | 1 | 3 | Heikkinen, Miss. Laina | female | 26.0 | 0 | 0 | STON/O2. 3101282 | 7.9250 | NaN | S |
| 3 | 4 | 1 | 1 | Futrelle, Mrs. Jacques Heath (Lily May Peel) | female | 35.0 | 1 | 0 | 113803 | 53.1000 | C123 | S |
| 4 | 5 | 0 | 3 | Allen, Mr. William Henry | male | 35.0 | 0 | 0 | 373450 | 8.0500 | NaN | S |
2.1.1 数据预处理
def read_dataset(fname):
# 指定第一列作为行索引
data = pd.read_csv(fname, index_col=0)
# 丢弃无用的数据
data.drop(['Name', 'Ticket', 'Cabin'], axis=1, inplace=True)
# 处理性别数据
data['Sex'] = (data['Sex'] == 'male').astype('int')
# 处理登船港口数据
labels = data['Embarked'].unique().tolist()
data['Embarked'] = data['Embarked'].apply(lambda n: labels.index(n))
# 处理缺失数据
data = data.fillna(0)
return data
train = read_dataset('E:/学习/机器学习/scikit-learn机器学习/code/datasets/titanic/train.csv')
train.head(6)
| Survived | Pclass | Sex | Age | SibSp | Parch | Fare | Embarked | |
|---|---|---|---|---|---|---|---|---|
| PassengerId | ||||||||
| 1 | 0 | 3 | 1 | 22.0 | 1 | 0 | 7.2500 | 0 |
| 2 | 1 | 1 | 0 | 38.0 | 1 | 0 | 71.2833 | 1 |
| 3 | 1 | 3 | 0 | 26.0 | 0 | 0 | 7.9250 | 0 |
| 4 | 1 | 1 | 0 | 35.0 | 1 | 0 | 53.1000 | 0 |
| 5 | 0 | 3 | 1 | 35.0 | 0 | 0 | 8.0500 | 0 |
| 6 | 0 | 3 | 1 | 0.0 | 0 | 0 | 8.4583 | 2 |
from sklearn.model_selection import train_test_split
y = train['Survived'].values
X = train.drop(['Survived'], axis=1).values
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
print("X_train:{}, X_test:{}, y_train:{}, y_test:{}".format(X_train.shape, X_test.shape, y_train.shape, y_test.shape))
X_train:(712, 7), X_test:(179, 7), y_train:(712,), y_test:(179,)
2.1.2 数据拟合与预测
from sklearn.tree import DecisionTreeClassifier
clf = DecisionTreeClassifier()
clf.fit(X_train,y_train)
train_score = clf.score(X_train,y_train)
test_score = clf.score(X_test,y_test)
print("train_score:{},test_score:{}".format(train_score,test_score))
train_score:0.9831460674157303,test_score:0.776536312849162
test = read_dataset('test.csv')
test.shape
(418, 7)
testpred = clf.predict(test)
test['Survived'] = testpred
test.head(10)
| Pclass | Sex | Age | SibSp | Parch | Fare | Embarked | Survived | |
|---|---|---|---|---|---|---|---|---|
| PassengerId | ||||||||
| 892 | 3 | 1 | 34.5 | 0 | 0 | 7.8292 | 0 | 0 |
| 893 | 3 | 0 | 47.0 | 1 | 0 | 7.0000 | 1 | 0 |
| 894 | 2 | 1 | 62.0 | 0 | 0 | 9.6875 | 0 | 0 |
| 895 | 3 | 1 | 27.0 | 0 | 0 | 8.6625 | 1 | 1 |
| 896 | 3 | 0 | 22.0 | 1 | 1 | 12.2875 | 1 | 1 |
| 897 | 3 | 1 | 14.0 | 0 | 0 | 9.2250 | 1 | 0 |
| 898 | 3 | 0 | 30.0 | 0 | 0 | 7.6292 | 0 | 0 |
| 899 | 2 | 1 | 26.0 | 1 | 1 | 29.0000 | 1 | 1 |
| 900 | 3 | 0 | 18.0 | 0 | 0 | 7.2292 | 2 | 1 |
| 901 | 3 | 1 | 21.0 | 2 | 0 | 24.1500 | 1 | 0 |
2.1.3 决策树可视化
from sklearn.tree import export_graphviz
with open("titanic.dot", 'w') as f:
f = export_graphviz(clf, out_file=f)
# 1. 在电脑上安装 graphviz
# 2. 运行 `dot -Tpng titanic.dot -o titanic.png`
# 3. 在当前目录查看生成的决策树 titanic.png
然后在终端输出命令dot -Tpng titanic.dot -o titanic.png即可:

ps:需要设置环境变量
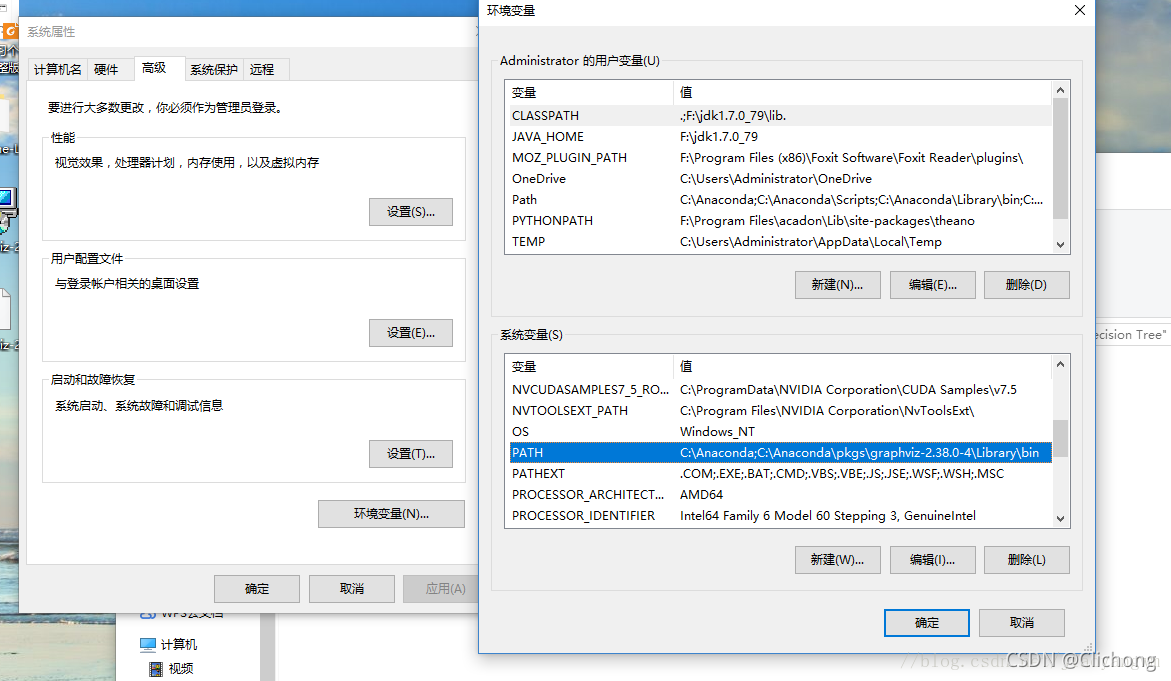
在“环境变量”中的“系统变量”中找到“PATH”,之后将路径C:\Anaconda\pkgs\graphviz-2.38.0-4\Library\bin添加到后面,重启Pycharm即可。
2.1.4 模型参数优化
使用GridSearchCV工具进行对参数评估
from sklearn.model_selection import GridSearchCV
thresholds = np.linspace(0, 0.005, 50)
# Set the parameters by cross-validation
param_grid = {'min_impurity_decrease': thresholds}
clf = GridSearchCV(DecisionTreeClassifier(), param_grid, cv=5, return_train_score=True)
clf.fit(X, y)
print("best param: {0}\nbest score: {1}".format(clf.best_params_,
clf.best_score_))
best param: {'min_impurity_decrease': 0.0011224489795918367}
best score: 0.8137216747222397
def plot_curve(train_sizes, cv_results, xlabel):
train_scores_mean = cv_results['mean_train_score']
train_scores_std = cv_results['std_train_score']
test_scores_mean = cv_results['mean_test_score']
test_scores_std = cv_results['std_test_score']
plt.figure(figsize=(10, 6), dpi=144)
plt.title('parameters turning')
plt.grid()
plt.xlabel(xlabel)
plt.ylabel('score')
plt.fill_between(train_sizes,
train_scores_mean - train_scores_std,
train_scores_mean + train_scores_std,
alpha=0.1, color="r")
plt.fill_between(train_sizes,
test_scores_mean - test_scores_std,
test_scores_mean + test_scores_std,
alpha=0.1, color="g")
plt.plot(train_sizes, train_scores_mean, '.--', color="r",
label="Training score")
plt.plot(train_sizes, test_scores_mean, '.-', color="g",
label="Cross-validation score")
plt.legend(loc="best")
plot_curve(thresholds, clf.cv_results_, xlabel='gini thresholds')
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-hQRfYB0z-1630936537313)(output_24_0.png)]](https://img-blog.csdnimg.cn/98567a364a334e6bac3765c35371398a.png?x-oss-process=image/watermark,type_ZHJvaWRzYW5zZmFsbGJhY2s,shadow_50,text_Q1NETiBAQ2xpY2hvbmc=,size_20,color_FFFFFF,t_70,g_se,x_16)
from sklearn.model_selection import GridSearchCV
entropy_thresholds = np.linspace(0, 0.01, 50)
gini_thresholds = np.linspace(0, 0.005, 50)
var = np.linspace(0,0.5,50)
# Set the parameters by cross-validation
param_grid = [
{'criterion': ['entropy'], 'min_impurity_decrease': entropy_thresholds},
{'criterion': ['gini'], 'min_impurity_decrease': gini_thresholds},
{'max_depth': range(2, 10)},
{'min_samples_split': range(2, 30, 2)},
{'min_samples_leaf': range(2,30,2)},
]
clf = GridSearchCV(DecisionTreeClassifier(), param_grid, cv=5, return_train_score=True)
clf.fit(X, y)
print("best param: {0}\nbest score: {1}".format(clf.best_params_,
clf.best_score_))
best param: {'min_samples_leaf': 8}
best score: 0.8249262444291003
2.2 决策树解决回归问题
在解决回归问题时,一时可能难以理解。因为本身决策树一般是用来解决分类任务的,但是如果区分的自己足够细,以致于在每一个区间段都有数值可以取,这里相当于将连续值离散化以实现回归预测。待落入小区间时再进行细化确定最后的预测值。
在这里使用预测波士顿房价为例子介绍,sklearn中有自带的波士顿房价数据集:
from sklearn.datasets import load_boston
boston = load_boston()
分别获得数据与标签
X = boston.data
y = boston.target
X.shape, y.shape
((506, 13), (506,))
可以获得输入特征名
boston.feature_names
array(['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD',
'TAX', 'PTRATIO', 'B', 'LSTAT'], dtype='<U7')
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import BaggingRegressor, AdaBoostRegressor, RandomForestRegressor, ExtraTreesRegressor
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.10)
X_train.shape, y_train.shape, X_test.shape, y_test.shape
((455, 13), (455,), (51, 13), (51,))
使用决策树进行回归拟合,
cls = DecisionTreeRegressor()
cls.fit(X_train, y_train)
trainscore = cls.score(X_train,y_train)
testscore = cls.score(X_test, y_test)
print("trainscore:{}, testscore:{}".format(trainscore, testscore))
trainscore:1.0, testscore:0.8006869992064902
预测与真实值之间的对比
testpred = cls.predict(X_test)
testpred,testpred.shape
(array([18.616, 7.971, 31.805, 14.509, 35.219, 21.286, 7.592, 14.331,
14.021, 22.632, 19.18 , 30.344, 36.261, 21.401, 19.119, 17.553,
23.189, 23.966, 26.453, 19.482, 8.925, 28.743, 31.395, 20.193,
20.038, 11.777, 24.309, 20.39 , 19.515, 21.522, 19.523, 31.538,
17.336, 27.974, 17.77 , 19.685, 23.374, 15.809, 43.124, 19.671,
18.355, 23.843, 21.21 , 15.566, 27.845, 14.647, 29.067, 23.775,
24.035, 23.813, 20.177]),
(51,))
y_test,y_test.shape
(array([19.6, 10.4, 33.2, 11.8, 36.4, 20.9, 10.5, 19.1, 14.6, 21.4, 18.8,
37. , 34.9, 21.7, 17.4, 20. , 23.2, 22.4, 25.1, 21.5, 5. , 30.7,
23.9, 19. , 19.9, 11.8, 29.1, 19.4, 23. , 22.6, 17.5, 23.6, 27.5,
30.8, 17.1, 17.8, 23.8, 16.7, 44. , 16.1, 18.7, 23. , 24.4, 13.3,
23.7, 13.1, 29.8, 25. , 28.7, 28.1, 18.3]),
(51,))
回归模型中score的判别式,计算的是预测系数 R 2 R^{2} R2:
u = (y_test-testpred)**2
u = u.sum()
u
506.8415439999994
v = (y_test-y_test.mean())**2
v = v.sum()
v
2819.9364705882344
R = 1-u/v
R
0.8202649069273986
决定系数(coefficient ofdetermination),有的教材上翻译为判定系数,也称为拟合优度。
决定系数反应了y的波动有多少百分比能被x的波动所描述,即表征依变数Y的变异中有多少百分比,可由控制的自变数X来解释。
意义:拟合优度越大,说明x对y的解释程度越高。自变量对因变量的解释程度越高,自变量引起的变动占总变动的百分比高。观察点在回归直线附近越密集。
使用的小Tips:
当样本数量少但是样本特征非常多的时候,决策树很容易过拟合,一般来说,样本数比特征数多一些会比较容易建立健壮的模型
如果样本数量少但是样本特征非常多,在拟合决策树模型前,推荐先做维度规约,比如主成分分析(PCA),特征选择(Losso)或者独立成分分析(ICA)。这样特征的维度会大大减小。再来拟合决策树模型效果会好。
在训练模型时,注意观察样本的类别情况(主要指分类树),如果类别分布非常不均匀,就要考虑用class_weight来限制模型过于偏向样本多的类别。
3. 集成算法
将多个分类器集成起来而形成的新的分类算法。这类算法又称元算法(meta-algorithm)。最常见的集成思想有两种bagging和boosting。
集成算法的原理是利用统计学采样原理,训练出成百上千个算法模型。当需要预测一个新样本时,使用这些模型分别对这个样本进行预测,然后采用多数服从少数原则,决定样本的类别。在scikit-learn中,所以的集成算法都实现在sklearn.ensemble包中。
这里分别使用使用集成算法进行分类与回归任务测试。
3.1 分类任务测试
from sklearn.ensemble import BaggingClassifier, AdaBoostClassifier, RandomForestClassifier, ExtraTreesClassifier
X_train.shape,y_train.shape
((712, 7), (712,))
X_test.shape,y_test.shape
((179, 7), (179,))
3.1.1 自助聚合Bagging算法
基于数据随机重抽样的分类器构建方法。
cls = BaggingClassifier()
cls.fit(X,y)
trainscore = cls.score(X_train,y_train)
testscore = cls.score(X_test,y_test)
print("trainscore:{},testscore:{}".format(trainscore,testscore))
trainscore:0.9747191011235955,testscore:0.9497206703910615
3.1.2 正向激励Boosting算法
基于错误提升分类器性能,通过集中关注被已有分类器分类错误的样本,构建新分类器并集成。
cls = AdaBoostClassifier()
cls.fit(X,y)
trainscore = cls.score(X_train,y_train)
testscore = cls.score(X_test,y_test)
print("trainscore:{},testscore:{}".format(trainscore,testscore))
trainscore:0.8384831460674157,testscore:0.7877094972067039
3.1.3 ExtraTrees算法
cls = ExtraTreesClassifier()
cls.fit(X,y)
trainscore = cls.score(X_train,y_train)
testscore = cls.score(X_test,y_test)
print("trainscore:{},testscore:{}".format(trainscore,testscore))
trainscore:0.9831460674157303,testscore:0.9776536312849162
3.1.4 随机森林
将训练集按照横(随机抽样本)、列(随机抽特征)进行有放回的随机抽取,获得n个新的训练集,训练出n个决策树,通过这n个树投票决定分类结果。主要的parameters 有n_estimators 和 max_features。
cls = RandomForestClassifier()
cls.fit(X,y)
trainscore = cls.score(X_train,y_train)
testscore = cls.score(X_test,y_test)
print("trainscore:{},testscore:{}".format(trainscore,testscore))
trainscore:0.9789325842696629,testscore:0.994413407821229
测试
test.drop(['Survived'], axis=1, inplace=True)
test.head(10)
| Pclass | Sex | Age | SibSp | Parch | Fare | Embarked | |
|---|---|---|---|---|---|---|---|
| PassengerId | |||||||
| 892 | 3 | 1 | 34.5 | 0 | 0 | 7.8292 | 0 |
| 893 | 3 | 0 | 47.0 | 1 | 0 | 7.0000 | 1 |
| 894 | 2 | 1 | 62.0 | 0 | 0 | 9.6875 | 0 |
| 895 | 3 | 1 | 27.0 | 0 | 0 | 8.6625 | 1 |
| 896 | 3 | 0 | 22.0 | 1 | 1 | 12.2875 | 1 |
| 897 | 3 | 1 | 14.0 | 0 | 0 | 9.2250 | 1 |
| 898 | 3 | 0 | 30.0 | 0 | 0 | 7.6292 | 0 |
| 899 | 2 | 1 | 26.0 | 1 | 1 | 29.0000 | 1 |
| 900 | 3 | 0 | 18.0 | 0 | 0 | 7.2292 | 2 |
| 901 | 3 | 1 | 21.0 | 2 | 0 | 24.1500 | 1 |
testpred = cls.predict(test)
test['Survived'] = testpred
输出预测结果
test.head()
| Pclass | Sex | Age | SibSp | Parch | Fare | Embarked | Survived | |
|---|---|---|---|---|---|---|---|---|
| PassengerId | ||||||||
| 892 | 3 | 1 | 34.5 | 0 | 0 | 7.8292 | 0 | 0 |
| 893 | 3 | 0 | 47.0 | 1 | 0 | 7.0000 | 1 | 0 |
| 894 | 2 | 1 | 62.0 | 0 | 0 | 9.6875 | 0 | 1 |
| 895 | 3 | 1 | 27.0 | 0 | 0 | 8.6625 | 1 | 0 |
| 896 | 3 | 0 | 22.0 | 1 | 1 | 12.2875 | 1 | 1 |
result = test.drop(['Pclass','Sex','Age','SibSp','Parch','Fare','Embarked'],axis=1)
result
| Survived | |
|---|---|
| PassengerId | |
| 892 | 0 |
| 893 | 0 |
| 894 | 1 |
| 895 | 0 |
| 896 | 1 |
| ... | ... |
| 1305 | 0 |
| 1306 | 1 |
| 1307 | 0 |
| 1308 | 0 |
| 1309 | 0 |
418 rows × 1 columns
输出了一个csv表格:
result.to_csv('test.csv')
在使用随机森林在kaggle提交之后,最后预测结果为0.74162
3.2 回归任务测试
随机森林进行回归预测
cls = RandomForestRegressor()
cls.fit(X_train, y_train)
trainscore = cls.score(X_train,y_train)
testscore = cls.score(X_test, y_test)
print("trainscore:{}, testscore:{}".format(trainscore, testscore))
trainscore:0.9839128821700205, testscore:0.8202649069273986
Bagging集成算法进行回归预测
cls = BaggingRegressor()
cls.fit(X_train, y_train)
trainscore = cls.score(X_train,y_train)
testscore = cls.score(X_test, y_test)
print("trainscore:{}, testscore:{}".format(trainscore, testscore))
trainscore:0.9698272722986764, testscore:0.7888720521864072
参考链接:
https://blog.csdn.net/jiaoyangwm/article/details/79525237