Piecewise Jerk Path Optimizer的python实现
Piecewise Jerk Path Optimizer的相关知识点可参考文末的两篇文章,本文主要是进行该算法的问题构造和实现。
cost function
J = w x ∑ i = 0 n ? 1 ( x i ? r i ) 2 + w x ′ ∑ i = 0 n ? 1 ( x i ′ ) 2 + w x ′ ′ ∑ i = 0 n ? 1 ( x i ′ ′ ) 2 + w x ′ ′ ′ ∑ i = 0 n ? 2 ( x i ′ ′ ′ ) 2 J=w_x\sum^{n-1}_{i=0}(x_i-r_i)^2+w_{x'}\sum^{n-1}_{i=0}(x'_i)^2+w_{x''}\sum^{n-1}_{i=0}(x''_i)^2+w_{x'''}\sum^{n-2}_{i=0}(x'''_i)^2 J=wx?i=0∑n?1?(xi??ri?)2+wx′?i=0∑n?1?(xi′?)2+wx′′?i=0∑n?1?(xi′′?)2+wx′′′?i=0∑n?2?(xi′′′?)2
qp problem
m i n { 1 2 x T P x + q x } l ≤ A x ≤ u min\{\frac{1}{2}x^TPx+qx\}\\l\le Ax\le u min{21?xTPx+qx}l≤Ax≤u
本文使用osqp进行二次规划问题的求解。
构造P和q矩阵
由 x i ′ ′ ′ Δ s = x i + 1 ′ ′ ? x i ′ ′ x'''_i\Delta s=x''_{i+1}-x''_i xi′′′?Δs=xi+1′′??xi′′?,得到 x i ′ ′ ′ = x i + 1 ′ ′ ? x i ′ ′ Δ s x'''_i=\frac{x''_{i+1}-x''_i}{\Delta s} xi′′′?=Δsxi+1′′??xi′′??,将其带入J中,可得
J = w x ∑ i = 0 n ? 1 [ ( x i ) 2 + ( r i ) 2 ? 2 x i r i ] + w x ′ ∑ i = 0 n ? 1 ( x i ′ ) 2 + w x ′ ′ ∑ i = 0 n ? 1 ( x i ′ ′ ) 2 + w x ′ ′ ′ Δ s 2 ∑ i = 0 n ? 2 [ ( x i + 1 ′ ′ ) 2 + ( x i ′ ′ ) 2 ? 2 x i + 1 ′ ′ x i ′ ′ ] J=w_x\sum^{n-1}_{i=0}[(x_i)^2+(r_i)^2-2x_ir_i]+w_{x'}\sum^{n-1}_{i=0}(x'_i)^2+w_{x''}\sum^{n-1}_{i=0}(x''_i)^2+\frac{w_{x'''}}{\Delta s^2}\sum^{n-2}_{i=0}[(x''_{i+1})^2+(x''_i)^2-2x''_{i+1}x''_i] J=wx?i=0∑n?1?[(xi?)2+(ri?)2?2xi?ri?]+wx′?i=0∑n?1?(xi′?)2+wx′′?i=0∑n?1?(xi′′?)2+Δs2wx′′′??i=0∑n?2?[(xi+1′′?)2+(xi′′?)2?2xi+1′′?xi′′?]
整理可得(去掉常数项):
J = w x ∑ i = 0 n ? 1 [ ( x i ) 2 ? 2 x i r i ] + w x ′ ∑ i = 0 n ? 1 ( x i ′ ) 2 + ( w x ′ ′ + 2 w x ′ ′ ′ Δ s 2 ) ∑ i = 0 n ? 1 ( x i ′ ′ ) 2 ? w x ′ ′ ′ Δ s 2 ( x 0 ′ ′ + x n ? 1 ′ ′ ) ? 2 w x ′ ′ ′ Δ s 2 ∑ i = 0 n ? 2 ( x i + 1 ′ ′ x i ′ ′ ) J=w_x\sum^{n-1}_{i=0}[(x_i)^2-2x_ir_i]+w_{x'}\sum^{n-1}_{i=0}(x'_i)^2+(w_{x''}+\frac{2w_{x'''}}{\Delta s^2})\sum^{n-1}_{i=0}(x''_i)^2-\frac{w_{x'''}}{\Delta s^2}(x''_0+x''_{n-1})-\frac{2w_{x'''}}{\Delta s^2}\sum^{n-2}_{i=0}(x''_{i+1}x''_i) J=wx?i=0∑n?1?[(xi?)2?2xi?ri?]+wx′?i=0∑n?1?(xi′?)2+(wx′′?+Δs22wx′′′??)i=0∑n?1?(xi′′?)2?Δs2wx′′′??(x0′′?+xn?1′′?)?Δs22wx′′′??i=0∑n?2?(xi+1′′?xi′′?)
令:
x = [ x 0 x 1 ? x n ? 1 x 0 ′ x 1 ′ ? x n ? 1 ′ x 0 ′ ′ x 1 ′ ′ ? x n ? 1 ′ ′ ] ∈ R 3 n × 1 x=\begin{bmatrix} x_0 \\[4pt] x_1\\[4pt]\vdots \\[4pt]x_{n-1}\\[4pt]x'_0\\[4pt]x'_1\\[4pt]\vdots\\[4pt]x'_{n-1}\\[4pt]x''_0\\[4pt]x''_1\\[4pt]\vdots\\[4pt]x''_{n-1} \end{bmatrix}\in R^{3n \times 1} x=???????????????????????????????x0?x1??xn?1?x0′?x1′??xn?1′?x0′′?x1′′??xn?1′′?????????????????????????????????∈R3n×1
则:
P x = [ w x 0 … 0 0 w x … 0 ? ? ? ? 0 0 … w x ] ∈ R n × n P_x=\begin{bmatrix} w_x &0& \ldots&0\\0&w_x&\ldots&0\\\vdots&\vdots&\ddots&\vdots\\0&0&\ldots&w_x \end{bmatrix}\in R^{n \times n} Px?=??????wx?0?0?0wx??0?……?…?00?wx????????∈Rn×n
P x ′ = [ w x ′ 0 … 0 0 w x ′ … 0 ? ? ? ? 0 0 … w x ′ ] ∈ R n × n P_{x'}=\begin{bmatrix} w_{x'} &0& \ldots&0\\0&w_{x'}&\ldots&0\\\vdots&\vdots&\ddots&\vdots\\0&0&\ldots&w_{x'} \end{bmatrix}\in R^{n \times n} Px′?=??????wx′?0?0?0wx′??0?……?…?00?wx′????????∈Rn×n
P x ′ ′ = [ w x ′ ′ + w x ′ ′ ′ Δ s 2 0 … 0 0 ? 2 w x ′ ′ ′ Δ s 2 w x ′ ′ + 2 w x ′ ′ ′ Δ s 2 … 0 0 ? ? ? ? ? 0 0 … w x ′ ′ + 2 w x ′ ′ ′ Δ s 2 0 0 0 … ? 2 w x ′ ′ ′ Δ s 2 w x ′ ′ + w x ′ ′ ′ Δ s 2 ] ∈ R n × n P_{x''}=\begin{bmatrix} w_{x''}+\frac{w_{x'''}}{\Delta s^2} &0& \ldots&0&0\\[8pt]-\frac{2w_{x'''}}{\Delta s^2}&w_{x''}+\frac{2w_{x'''}}{\Delta s^2}&\ldots&0&0\\[8pt]\vdots&\vdots&\ddots&\vdots&\vdots\\[8pt]0&0&\ldots&w_{x''}+\frac{2w_{x'''}}{\Delta s^2}&0\\[8pt]0&0&\ldots&-\frac{2w_{x'''}}{\Delta s^2}&w_{x''}+\frac{w_{x'''}}{\Delta s^2} \end{bmatrix}\in R^{n \times n} Px′′?=??????????????wx′′?+Δs2wx′′′???Δs22wx′′′???00?0wx′′?+Δs22wx′′′???00?……?……?00?wx′′?+Δs22wx′′′???Δs22wx′′′???00?0wx′′?+Δs2wx′′′?????????????????∈Rn×n
P = [ P x 0 0 0 P x ′ 0 0 0 P x ′ ′ ] ∈ R 3 n × 3 n P=\begin{bmatrix} P_x &0&0\\0&P_{x'}&0\\0&0&P_{x''} \end{bmatrix}\in R^{3n \times 3n} P=???Px?00?0Px′?0?00Px′′?????∈R3n×3n
q = [ ? r 0 ? r 1 ? ? r n ? 1 0 ? 0 ] T ∈ R 1 × 3 n q=\begin{bmatrix} -r_0\\-r_1\\\vdots\\-r_{n-1}\\0\\\vdots\\0 \end{bmatrix}^T\in R^{1 \times 3n} q=??????????????r0??r1???rn?1?0?0??????????????T∈R1×3n
构造不等式矩阵
x i + 1 = x i + x i ′ Δ s + 1 2 Δ s 2 x i ′ ′ + 1 6 Δ s 3 x i ′ ′ ′ x_{i+1}=x_i+x'_i\Delta s+\frac{1}{2}\Delta s^2x''_i+\frac{1}{6}\Delta s^3x'''_i xi+1?=xi?+xi′?Δs+21?Δs2xi′′?+61?Δs3xi′′′?
x i + 1 ′ = x i ′ + x i ′ ′ Δ s + 1 2 Δ s 2 x i ′ ′ ′ x'_{i+1}=x'_i+x''_i\Delta s+\frac{1}{2}\Delta s^2x'''_i xi+1′?=xi′?+xi′′?Δs+21?Δs2xi′′′?
将 x i ′ ′ ′ x'''_i xi′′′?提取出来,可以得到:
x i ′ ′ ′ Δ s 3 6 = x i + 1 ? x i ? x i ′ Δ s ? 1 2 Δ s 2 x i ′ ′ x'''_i\frac{\Delta s^3}{6}=x_{i+1}-x_i-x'_i\Delta s-\frac{1}{2}\Delta s^2x''_i xi′′′?6Δs3?=xi+1??xi??xi′?Δs?21?Δs2xi′′?
x i ′ ′ ′ Δ s 2 2 = x i + 1 ′ ? x i ′ ? x i ′ ′ Δ s x'''_i\frac{\Delta s^2}{2}=x'_{i+1}-x'_i-x''_i\Delta s xi′′′?2Δs2?=xi+1′??xi′??xi′′?Δs
令
A x = I ∈ R 3 n × 3 n A_x=I \in R^{3n\times3n} Ax?=I∈R3n×3n
A d s = ? Δ s I ∈ R n × n A_{ds}=-\Delta sI \in R^{n\times n} Ads?=?ΔsI∈Rn×n
A d s 2 = ? 1 2 Δ s 2 I ∈ R n × n A_{ds^2}=-\frac{1}{2}\Delta s^2I \in R^{n\times n} Ads2?=?21?Δs2I∈Rn×n
A I = [ ? 1 1 0 … 0 0 ? 1 1 … 0 ? ? ? ? ? 0 0 … ? 1 1 0 0 … 0 ? 1 ] ∈ R n × n A_{I}=\begin{bmatrix} -1 &1& 0&\ldots&0 \\0&-1&1&\ldots&0 \\\vdots&\vdots&\ddots&\ddots&\vdots \\0&0&\ldots&-1&1 \\0&0&\ldots&0&-1 \end{bmatrix}\in R^{n \times n} AI?=?????????10?00?1?1?00?01?……?……??10?00?1?1?????????∈Rn×n
A = [ A x A I A d s A d s 2 0 A I A d s ] ∈ R 5 n × 3 n A=\begin{bmatrix} &A_x\\A_I&A_{ds}&A_{ds^2} \\0&A_I&A_{ds} \end{bmatrix}\in R^{5n \times 3n} A=???AI?0?Ax?Ads?AI??Ads2?Ads?????∈R5n×3n
上下边界:
l = [ x 0 l ? x ( n ? 1 ) l x 0 l ′ ? x ( n ? 1 ) l ′ x 0 l ′ ′ ? x ( n ? 1 ) l ′ ′ ? Δ s 3 6 x b o u n d ′ ′ ′ ? ? Δ s 3 6 x b o u n d ′ ′ ′ ? Δ s 2 2 x b o u n d ′ ′ ′ ? ? Δ s 2 2 x b o u n d ′ ′ ′ ] ∈ R 5 n × 1 l=\begin{bmatrix} x_{0l}\\[8pt]\vdots \\[8pt]x_{(n-1)l}\\[8pt]x'_{0l}\\[8pt]\vdots\\[8pt]x'_{(n-1)l}\\[8pt]x''_{0l}\\[8pt]\vdots\\[8pt]x''_{(n-1)l}\\[8pt]-\frac{\Delta s^3}{6}x'''_{bound}\\[8pt]\vdots\\[8pt]-\frac{\Delta s^3}{6}x'''_{bound}\\[8pt]-\frac{\Delta s^2}{2}x'''_{bound}\\[8pt]\vdots\\[8pt]-\frac{\Delta s^2}{2}x'''_{bound} \end{bmatrix}\in R^{5n \times 1} l=????????????????????????????????????????????????????x0l??x(n?1)l?x0l′??x(n?1)l′?x0l′′??x(n?1)l′′??6Δs3?xbound′′′???6Δs3?xbound′′′??2Δs2?xbound′′′???2Δs2?xbound′′′??????????????????????????????????????????????????????∈R5n×1
u = [ x 0 u ? x ( n ? 1 ) u x 0 u ′ ? x ( n ? 1 ) u ′ x 0 u ′ ′ ? x ( n ? 1 ) u ′ ′ Δ s 3 6 x b o u n d ′ ′ ′ ? Δ s 3 6 x b o u n d ′ ′ ′ Δ s 2 2 x b o u n d ′ ′ ′ ? Δ s 2 2 x b o u n d ′ ′ ′ ] ∈ R 5 n × 1 u=\begin{bmatrix} x_{0u}\\[8pt]\vdots \\[8pt]x_{(n-1)u}\\[8pt]x'_{0u}\\[8pt]\vdots\\[8pt]x'_{(n-1)u}\\[8pt]x''_{0u}\\[8pt]\vdots\\[8pt]x''_{(n-1)u}\\[8pt]\frac{\Delta s^3}{6}x'''_{bound}\\[8pt]\vdots\\[8pt]\frac{\Delta s^3}{6}x'''_{bound}\\[8pt]\frac{\Delta s^2}{2}x'''_{bound}\\[8pt]\vdots\\[8pt]\frac{\Delta s^2}{2}x'''_{bound} \end{bmatrix}\in R^{5n \times 1} u=????????????????????????????????????????????????????x0u??x(n?1)u?x0u′??x(n?1)u′?x0u′′??x(n?1)u′′?6Δs3?xbound′′′??6Δs3?xbound′′′?2Δs2?xbound′′′??2Δs2?xbound′′′??????????????????????????????????????????????????????∈R5n×1
构造好矩阵后,使用Python实现
import matplotlib.pyplot as plt
import osqp
import numpy as np
from scipy import sparse
import random
# 障碍物设置
obs = [[5,10,2,3],[15,20,-2,-0.5],[25,30,0,1]]#start_s,end_s,l_low,l_up
s_len = 50
delta_s = 0.1
n = int(s_len / delta_s)
x = np.linspace(0,s_len,n)
up_bound = [0]*(5*n + 3)
low_bound = [0]*(5*n + 3)
s_ref = [0]*3*n
dddl_bound = 0.01
####################边界提取################
l_bound = 5
for i in range(n):
for j in range(len(obs)):
if x[i] >= obs[j][0] and x[i] <= obs[j][1]:
low_ = obs[j][2]
up_ = obs[j][3]
break
else:
up_ = l_bound
low_ = -l_bound
up_bound[i] = up_
low_bound[i] = low_
s_ref[i] = 0.5*(up_ + low_)
# cotinue_i = True
# for i in range(n):
# x_tmp = x[i]
# if cotinue_i:
# i_start = i
# up_ = random.randint(1, 3) * 0.1
# low_ = random.randint(-3, -1) * 0.1
# if up_ < low_:
# tmp = up_
# up_ = low_
# low_ = tmp
# cotinue_i = False
# if i - i_start >= obs_len / delta_s:
# cotinue_i = True
# up_bound[i] = up_
# low_bound[i] = low_
# s_ref[i] = 0.5*(up_ + low_)
for i in range(3*n,4*n):
up_bound[i] = dddl_bound * delta_s *delta_s *delta_s/6
low_bound[i] = -dddl_bound * delta_s *delta_s *delta_s/6
for i in range(4*n,5*n):
up_bound[i] = dddl_bound * delta_s *delta_s / 2
low_bound[i] = -dddl_bound * delta_s *delta_s / 2
####################构造P和Q################
w_l = 0.005
w_dl = 1
w_ddl = 1
w_dddl = 0.1
eye_n = np.identity(n)
zero_n = np.zeros((n, n))
P_zeros = zero_n
P_l = w_l * eye_n
P_dl = w_dl * eye_n
P_ddl = (w_ddl + 2*w_dddl/delta_s/delta_s) * eye_n -2 * w_dddl / delta_s/delta_s* np.eye(n,k = -1)
P_ddl[0][0] = w_ddl + w_dddl/delta_s/delta_s
P_ddl[n-1][n-1] = w_ddl + w_dddl/delta_s/delta_s
P = sparse.csc_matrix(np.block([
[P_l,P_zeros,P_zeros],
[P_zeros,P_dl,P_zeros],
[P_zeros,P_zeros,P_ddl]
]))
q = np.array([-w_l*s_ for s_ in s_ref])
####################构造A和LU################
#构造:l(i+1) = l(i) + l'(i) * delta_s + 1/2 * l''(i) * delta_s^2 + 1/6 * l'''(i) * delta_s^3
A_ll = -eye_n + np.eye(n,k = 1)
A_ldl = -delta_s * eye_n
A_lddl = -0.5 * delta_s * delta_s * eye_n
A_l = (np.block([
[A_ll,A_ldl,A_lddl]
]))
# 构造:l'(i+1) = l'(i) + l''(i) * delta_s + 1/2 * l'''(i) * delta_s^2
A_dll = zero_n
A_dldl = -eye_n + np.eye(n,k = 1)
A_dlddl = -delta_s * eye_n
A_dl = np.block([
[A_dll,A_dldl,A_dlddl]
])
A_ul = np.block([
[eye_n,zero_n,zero_n],
[zero_n,zero_n,zero_n],
[zero_n,zero_n,zero_n]
])#3n*3n
# 初始化设置
A_init = np.zeros((3, 3*n))
A_init[0][0] = 1
A = sparse.csc_matrix(np.row_stack((A_ul,A_l,A_dl,A_init)))
low_bound[5*n] = 1
up_bound[5*n] = 1
l = np.array(low_bound)
u = np.array(up_bound)
# Create an OSQP object
prob = osqp.OSQP()
# Setup workspace and change alpha parameter
prob.setup(P, q, A, l, u, alpha=1.0)
# Solve problem
res = prob.solve()
plt.plot(u[:n],'.',color = 'blue')
plt.plot(l[:n],'.',color = 'black')
# plt.plot(s_ref[:n],'.')
plt.plot(res.x[:n],'.',color = 'red')
plt.show()
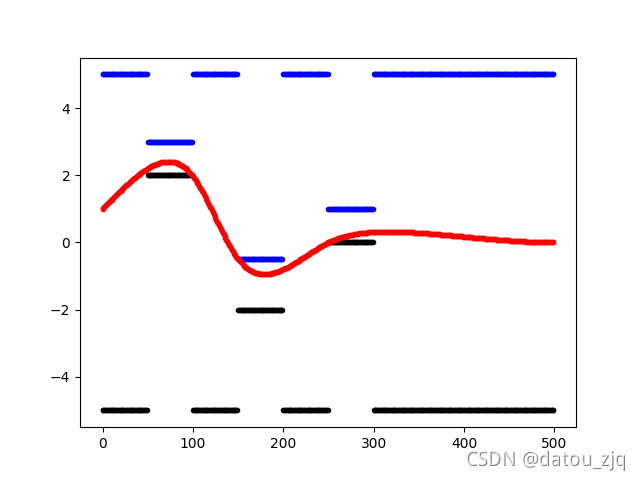
规划结果如上图所示,其中蓝色为上边界曲线,黑色为下边,红色为规划出的轨迹。
参考文章: