[数据结构与算法]围圈抽牌报数问题

问题描述

米免参加公司司建，100个同事围坐圈，裁判开始顺时针从头发牌，每发3张白牌就会发出1张黑
牌，抽到黑牌的人出局，每局第N个抽到黑牌的将获得奖励。问如果米免想获得奖品，需要坐在最
开始100人里第几个位置?
输入描述

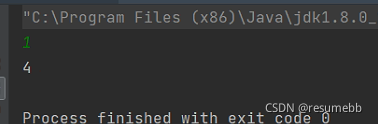
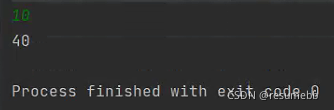
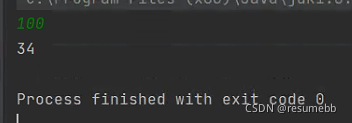
正整数N,表示要计算的为第N个抽到黑牌的同学，0< N ≤?100
输出描述

第N个抽到黑牌的同学在最开始100人里的位置(1 ~100).

思路：

典型的约瑟夫环问题，构建环形链表，遍历环形链表会是一个无限循环，如果链表中的数据逐渐减少，不控制终究会一个不剩，这又不满足我们问题的求解，因此我们需要定义出循环结束的条件，按照约瑟夫环的规则，只剩下一个的时候就结束，在环形链表结构中，那就是结点本身的下一个节点就是它自己，这样就可以结束遍历了，最后返回最后一个结点，循环条件只要环形链表还有一个元素就进行循环，每一次都发一张白牌，也就是跳过不进行操作，发了三次后的下一次就是黑牌，同时采用计数器判断本次黑牌是不是需要的N，如果是直接return本次的data，否则的话就删掉本节点，继续循环。
?

import java.util.Scanner;

class Node{
    int data;
    Node next;
    public Node(){}
    public Node(int data){this.data = data;}
}

class JosefCircleMain {
    public static int count(int n, int num){
        int k = 3,count=0;
        Node head = new Node();
        Node cur = head;
        for(int i=1;i<=n;i++){
            Node node = new Node(i);
            cur.next = node;
            cur = node;
        }
        cur.next = head.next;
        Node p = head.next;
        while(p.next!=p){
            for(int i=1;i<k;i++){
                p = p.next;
            }
            count++;
            if(count == num){
                return (int)(p.next.data);
            }
            //当数到3的时候，出局
            p.next = p.next.next;
            p = p.next;
        }
        return p.next.data;
    }
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int num = in.nextInt();
        System.out.println(count(100, num));
    }
}

?

?