[数据结构与算法]PAT 甲级 树（二）

AVL两道题的思路待补充，红黑树待写！！！

二叉搜索树最后两层节点数量

题目

二叉搜索树 (BST) 递归定义为具有以下属性的二叉树：

若它的左子树不空，则左子树上所有结点的值均小于或等于它的根结点的值
若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值
它的左、右子树也分别为二叉搜索树
将一系列数字按顺序插入到一个空的二叉搜索树中，然后，请你计算结果树的最低两层的结点个数。

输入格式
第一行包含整数 N，表示插入数字序列包含的数字个数。

第二行包含 N 个整数，表示插入数字序列。

输出格式
以如下格式，在一行中，输出结果树的最后两层的结点数：

n1 + n2 = n
n1 是最底层结点数量，n2 是倒数第二层结点数量，n 是它们的和。

数据范围
1≤N≤1000,
?1000≤ 插入数字 ≤1000。

输入样例：
9
25 30 42 16 20 20 35 -5 28
输出样例：
2 + 4 = 6

思想

1、如何根据序列插入二叉搜索树中

void insert(int& u, int w)
{
    if (!u)
    {
        u = ++ idx;
        v[u] = w;
    }
    else if (w <= v[u]) insert(l[u], w);
    else insert(r[u], w);
}

2、如何记录每一层的节点数量
（1）y总的做法——dfs ，记录深度

void dfs(int u, int depth)
{
    if (!u) return;
    cnt[depth] ++ ;
    max_depth = max(max_depth, depth);
    dfs(l[u], depth + 1);
    dfs(r[u], depth + 1);
}

（2） 我的做法——层序遍历

    queue<PII> q;
    q.push({0, 1});
    int cnt[N], max_level = 0;
    while(q.size()){
        int top = q.front().first;
        int level = q.front().second;
        q.pop();
        cnt[level] ++;
        max_level = max(level, max_level);
        if(l[top] != -1) {
            q.push({l[top], level + 1});
        }
        if(r[top] != -1) {
            q.push({r[top], level + 1});
        }
    }

自己的代码

#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
const int N = 1e3 + 10;
int tr[N], l[N], r[N], a[N];
int idx = 0;
typedef pair<int, int> PII;
void insert(int u, int k){
    if(k <= tr[u]) {
        if(l[u] != -1)
            insert(l[u], k);
        else{
            l[u] = ++idx;
            tr[idx] = k;
        }
    }
    else{
        if(r[u] != -1)
            insert(r[u], k);
        else{
            r[u] = ++idx;
            tr[idx] = k;
        }
    }
}
int main(){
    int n, i;
    cin>>n;
    memset(l, -1, sizeof l);
    memset(r, -1, sizeof r);
    int root = 0;
    for(i = 0; i < n; i ++){
        cin>>a[i];
        if(!i) tr[root] = a[i];
        else insert(root, a[i]);
    }
    
    //层序遍历
    queue<PII> q;
    q.push({0, 1});
    int cnt[N], max_level = 0;
    while(q.size()){
        int top = q.front().first;
        int level = q.front().second;
        q.pop();
        cnt[level] ++;
        max_level = max(level, max_level);
        if(l[top] != -1) {
            q.push({l[top], level + 1});
        }
        if(r[top] != -1) {
            q.push({r[top], level + 1});
        }
    }
    printf("%d + %d = %d", cnt[max_level], cnt[max_level - 1], cnt[max_level] + cnt[max_level - 1]);
}

y总的代码

#include <iostream>

using namespace std;

const int N = 1010;

int n;
int l[N], r[N], v[N], idx;
int cnt[N], max_depth;

void insert(int& u, int w)
{
    if (!u)
    {
        u = ++ idx;
        v[u] = w;
    }
    else if (w <= v[u]) insert(l[u], w);
    else insert(r[u], w);
}

void dfs(int u, int depth)
{
    if (!u) return;
    cnt[depth] ++ ;
    max_depth = max(max_depth, depth);
    dfs(l[u], depth + 1);
    dfs(r[u], depth + 1);
}

int main()
{
    cin >> n;

    int root = 0;
    for (int i = 0; i < n; i ++ )
    {
        int w;
        cin >> w;
        insert(root, w);
    }

    dfs(root, 0);

    int n1 = cnt[max_depth], n2 = cnt[max_depth - 1];
    printf("%d + %d = %d\n", n1, n2, n1 + n2);

    return 0;
}

作者：yxc
链接：https://www.acwing.com/activity/content/code/content/283562/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

前序和后序遍历

题目

假设一个二叉树上所有结点的权值都互不相同。

我们可以通过后序遍历和中序遍历来确定唯一二叉树。

也可以通过前序遍历和中序遍历来确定唯一二叉树。

但是，如果只通过前序遍历和后序遍历，则有可能无法确定唯一二叉树。

现在，给定一组前序遍历和后序遍历，请你输出对应二叉树的中序遍历。

如果树不是唯一的，则输出任意一种可能树的中序遍历即可。

输入格式
第一行包含整数 N，表示结点数量。

第二行给出前序遍历序列。

第三行给出后序遍历序列。

一行中的数字都用空格隔开。

输出格式
首先第一行，如果树唯一，则输出 Yes，如果不唯一，则输出 No。

然后在第二行，输出树的中序遍历。

注意，如果树不唯一，则输出任意一种可能的情况均可。

数据范围
1≤N≤30
输入样例1：
7
1 2 3 4 6 7 5
2 6 7 4 5 3 1
输出样例1：
Yes
2 1 6 4 7 3 5
输入样例2：
4
1 2 3 4
2 4 3 1
输出样例2：
No
2 1 3 4

思想

关键：找到不同遍历之间的特点！

// 先序遍历是根左右，后序遍历是左右根，我们没法判断左子树在哪里结束，于是我们通过枚举的方式,去递归遍历
// 枚举左子树在不同位置结束的时候的方案数，如果方案数 > 1,说明不唯一
// 同时在过程中，由于每次遍历左右子树，于是我们可以借此求得中序遍历。

自己的代码

//  先序遍历是根左右，后序遍历是左右根，我们没法判断左子树在哪里结束，于是我们通过枚举的方式,去递归遍历
// 枚举左子树在不同位置结束的时候的方案数，如果方案数 > 1,说明不唯一
// 同时在过程中，由于每次遍历左右子树，于是我们可以借此求得中序遍历。

#include<iostream>
using namespace std;
const int N = 40;
int pre[N], post[N];
int dfs(int l1, int r1, int l2, int r2, string& in){
    //l1是pre， l2是post
    if(l1 > r1) return 1;//注意这里是return 1
    if(pre[l1] != post[r2]) return 0;
    
    int cnt = 0;
    for (int i = l1; i <= r1; i ++ ){//按理来说，i应该是从l1 + 1开始的，但是如果改成l1 + 1，就会报错
        string lin, rin;
        int lcnt = dfs(l1 + 1, i, l2, l2 + i - l1 - 1, lin);
        int rcnt = dfs(i + 1, r1, l2 + i - l1 , r2 - 1, rin);
        if(lcnt && rcnt){
            cnt += lcnt * rcnt;
            in = lin + to_string(pre[l1]) + ' ' + rin;
            if(cnt > 1) break;
        }
    }
    return cnt;
}
int main(){
    int n, i;
    cin>>n;
    for(i = 0; i < n; i ++) cin>>pre[i];
    for(i = 0; i < n; i ++) cin>>post[i];
    
    string in;
    int cnt = dfs(0, n - 1, 0, n - 1, in);

    if (cnt > 1) puts("No");
    else puts("Yes");
    
    in.pop_back();//会多一个空格，所以要pop_back
    cout << in << endl;
}

y总的代码

#include <iostream>

using namespace std;

const int N = 40;

int n;
int pre[N], post[N];

int dfs(int l1, int r1, int l2, int r2, string& in)
{
    if (l1 > r1) return 1;
    if (pre[l1] != post[r2]) return 0;

    int cnt = 0;
    for (int i = l1; i <= r1; i ++ )  // 枚举左子树包含的节点数量
    {
        string lin, rin;
        int lcnt = dfs(l1 + 1, i, l2, l2 + i - l1 - 1, lin);
        int rcnt = dfs(i + 1, r1, l2 + i - l1 - 1 + 1, r2 - 1, rin);

        if (lcnt && rcnt)
        {
            in = lin + to_string(pre[l1]) + ' ' + rin;
            cnt += lcnt * rcnt;
            if (cnt > 1) break;
        }
    }

    return cnt;
}

int main()
{
    cin >> n;
    for (int i = 0; i < n; i ++ ) cin >> pre[i];
    for (int i = 0; i < n; i ++ ) cin >> post[i];

    string in;    
    int cnt = dfs(0, n - 1, 0, n - 1, in);

    if (cnt > 1) puts("No");
    else puts("Yes");

    in.pop_back();
    cout << in << endl;

    return 0;
}

作者：yxc
链接：https://www.acwing.com/activity/content/code/content/283585/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

Z字形遍历二叉树

题目

假设一个二叉树上各结点的权值互不相同。

我们就可以通过其后序遍历和中序遍历来确定唯一二叉树。

请你输出该二叉树的 Z 字形遍历序列----也就是说，从根结点开始，逐层遍历，第一层从右到左遍历，第二层从左到右遍历，第三层从右到左遍历，以此类推。

例如，下图所示二叉树，其 Z 字形遍历序列应该为：1 11 5 8 17 12 20 15。

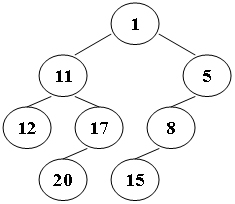
输入格式
第一行包含整数 N，表示二叉树结点数量。

第二行包含 N 个整数，表示二叉树的中序遍历序列。

第三行包含 N 个整数，表示二叉树的后序遍历序列。

输出格式
输出二叉树的 Z 字形遍历序列。

数据范围
1≤N≤30
输入样例：
8
12 11 20 17 1 15 8 5
12 20 17 11 15 8 5 1
输出样例：
1 11 5 8 17 12 20 15

思想

1、给定二叉树中序遍历和后序遍历，重建二叉树

int build(int il, int ir, int pl, int pr)
{
    int root = post[pr];
    int k = pos[root];

    if (il < k) l[root] = build(il, k - 1, pl, pl + k - 1 - il);
    if (k < ir) r[root] = build(k + 1, ir, pl + k - 1 - il + 1, pr - 1);

    return root;
}

2、Z字形层序遍历
只有在偶数层时翻转即可

reverse函数的使用，第二个形参是最后一位的下一个位置

void bfs(int root)
{
    int hh = 0, tt = 0;
    q[0] = root;

    int step = 0;
    while (hh <= tt)
    {
        int head = hh, tail = tt;
        while (hh <= tail)
        {
            int t = q[hh ++ ];
            if (l.count(t)) q[ ++ tt] = l[t];
            if (r.count(t)) q[ ++ tt] = r[t];
        }

        if ( ++ step % 2) reverse(q + head, q + tail + 1);
    }
}

自己的代码

//y总的
//y总的思路，将奇数层的翻转即可
#include <iostream>
#include <algorithm>
#include <unordered_map>

using namespace std;

using namespace std;

const int N = 40;

int n;
unordered_map<int, int> l, r, pos;
int in[N], post[N];
int q[N];

int build(int il, int ir, int pl, int pr)
{
    int root = post[pr];
    int k = pos[root];

    if (il < k) l[root] = build(il, k - 1, pl, pl + k - 1 - il);
    if (k < ir) r[root] = build(k + 1, ir, pl + k - 1 - il + 1, pr - 1);

    return root;
}
//这里记录了如何写出层序遍历每一层的写法，q即为层序遍历结果
void bfs(int root){
    int hh = 0, tt = 0;
    q[0] = root;
    int step = 0;
    while(hh <= tt){
        int head = hh, tail = tt;
        while(hh <= tail){//只遍历到上一层添加到的tt处
            int t = q[hh ++];
            if (l.count(t)) q[ ++ tt] = l[t];
            if (r.count(t)) q[ ++ tt] = r[t];
        }
        if(++ step % 2 == 1) reverse(q + head, q + tail + 1);
    }
}
int main()
{
    cin >> n;
    for (int i = 0; i < n; i ++ )
    {
        cin >> in[i];
        pos[in[i]] = i;
    }
    for (int i = 0; i < n; i ++ ) cin >> post[i];

    int root = build(0, n - 1, 0, n - 1);

    bfs(root);

    cout << q[0];
    for (int i = 1; i < n; i ++ ) cout << ' ' << q[i];
    cout << endl;

    return 0;
}




//自己的代码
/*#include <iostream>
#include <cstring>
#include <queue>
#include <stack>
using namespace std;
const int N = 1e4 + 10;
int post[N], in[N], r[N], l[N], pos[N];
typedef pair<int, int> PII;
int build(int l1, int r1, int l2, int r2){
    if(l1 > r1) return false;
    int root = post[r2];
    int k = pos[root];
    
    if(l1 < k) l[root] = build(l1, k - 1, l2, l2 + k - 1- l1);
    if(k < r1) r[root] = build(k + 1, r1, l2 + k - l1, r2 - 1);
    
    return root;
}
int main(){
    int n;
    cin>>n;
    for (int i = 0; i < n; i ++ )
    {
        cin >> in[i];
        pos[in[i]] = i;
    }
    for(int i = 0; i < n; i ++) cin>>post[i];
    memset(l, -1, sizeof l);
    memset(r, -1, sizeof r);
    
    int root = build(0, n - 1, 0, n - 1);
    
    queue<PII> q;
    q.push({root, 1});
    //cout<<root;
    int before_level = 1;
    string str;
    queue<PII> a;
    while(q.size()){
        int top = q.front().first;
        int level = q.front().second;
        if(before_level != level){
            if(level % 2 ==  1){
                //reverse(q);
                a = q;
                stack<PII> s;
                while(a.size()){
                    s.push(a.front());
                    a.pop();
                }
                while(s.size()){
                    a.push(s.top());
                    s.pop();
                }
            }
        }
        if(level > 2 && level % 2 == 1){
            str += to_string(a.front().first) + " ";
            a.pop();
        }
        else str += to_string(top) + " ";
        //cout<<top<<endl;
        q.pop();
        before_level = level;
        if(l[top] != -1)
            q.push({l[top], level + 1});
        if(r[top] != -1)
            q.push({r[top], level + 1});
    }
    str.pop_back();
    cout<<str<<endl;
}*/

y总的代码

#include <iostream>
#include <algorithm>
#include <unordered_map>

using namespace std;

using namespace std;

const int N = 40;

int n;
unordered_map<int, int> l, r, pos;
int in[N], post[N];
int q[N];

int build(int il, int ir, int pl, int pr)
{
    int root = post[pr];
    int k = pos[root];

    if (il < k) l[root] = build(il, k - 1, pl, pl + k - 1 - il);
    if (k < ir) r[root] = build(k + 1, ir, pl + k - 1 - il + 1, pr - 1);

    return root;
}

void bfs(int root)
{
    int hh = 0, tt = 0;
    q[0] = root;

    int step = 0;
    while (hh <= tt)
    {
        int head = hh, tail = tt;
        while (hh <= tail)
        {
            int t = q[hh ++ ];
            if (l.count(t)) q[ ++ tt] = l[t];
            if (r.count(t)) q[ ++ tt] = r[t];
        }

        if ( ++ step % 2) reverse(q + head, q + tail + 1);
    }
}

int main()
{
    cin >> n;
    for (int i = 0; i < n; i ++ )
    {
        cin >> in[i];
        pos[in[i]] = i;
    }
    for (int i = 0; i < n; i ++ ) cin >> post[i];

    int root = build(0, n - 1, 0, n - 1);

    bfs(root);

    cout << q[0];
    for (int i = 1; i < n; i ++ ) cout << ' ' << q[i];
    cout << endl;

    return 0;
}

作者：yxc
链接：https://www.acwing.com/activity/content/code/content/283592/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

后序遍历

题目

假设二叉树上各结点的权值互不相同且都为正整数。

给定二叉树的前序遍历和中序遍历，请你输出二叉树的后序遍历的第一个数字。

输入格式
第一行包含整数 N，表示二叉树结点总数。

第二行给出二叉树的前序遍历序列。

第三行给出二叉树的中序遍历序列。

输出格式
输出二叉树的后序遍历的第一个数字。

数据范围
1≤N≤50000
输入样例：
7
1 2 3 4 5 6 7
2 3 1 5 4 7 6
输出样例：
3

思想

自己的代码

//这题要用哈希表来存，不能用遍历来找root的下标，会超时
//其他题，也可能用哈希表存l，和r， 因为不知道节点的值多大，有可能很大
#include<iostream>
#include <unordered_map>
using namespace std;
unordered_map<int,int> pos;
int post = 0;
const int N = 1e5 + 10;
int pre[N], in[N];
void build(int pl, int pr, int il, int ir){
    int root = pre[pl];
    int k = pos[root];
    if(il < k) build(pl + 1, pl + + 1 + k - 1 - il, il, k - 1);
    if(k < ir) build(pl + 1 + k - 1 - il + 1, pr, k + 1, ir);
    
    if(!post) post = root;//第一个return的就是它
}
int main(){
    int n;
    cin>>n;
    for (int i = 0; i < n; i ++ ) cin >> pre[i];
    for (int i = 0; i < n; i ++ )
    {
        cin >> in[i];
        pos[in[i]] = i;
    }
    build(0, n - 1, 0, n - 1);
    cout<<post<<endl;
}

y总的代码

#include <iostream>
#include <unordered_map>

using namespace std;

const int N = 50010;

int n;
int pre[N], in[N];
unordered_map<int, int> pos;
int post;

void build(int il, int ir, int pl, int pr)
{
    int root = pre[pl];
    int k = pos[root];

    if (il < k) build(il, k - 1, pl + 1, pl + 1 + k - 1 - il);
    if (k < ir) build(k + 1, ir, pl + 1 + k - 1 - il + 1, pr);

    if (!post) post = root;
}

int main()
{
    cin >> n;

    for (int i = 0; i < n; i ++ ) cin >> pre[i];
    for (int i = 0; i < n; i ++ )
    {
        cin >> in[i];
        pos[in[i]] = i;
    }

    build(0, n - 1, 0, n - 1);

    cout << post << endl;
    return 0;
}

作者：yxc
链接：https://www.acwing.com/activity/content/code/content/283601/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

AVL树的根

题目

AVL树是一种自平衡二叉搜索树。

在AVL树中，任何节点的两个子树的高度最多相差 1 个。

如果某个时间，某节点的两个子树之间的高度差超过 1，则将通过树旋转进行重新平衡以恢复此属性。

图 1?4 说明了旋转规则。

31.jpg 32.jpg
33.jpg 34.jpg

现在，给定插入序列，请你求出 AVL 树的根是多少。

输入格式
第一行包含整数 N，表示总插入值数量。

第二行包含 N 个不同的整数，表示每个插入值。

输出格式
输出得到的 AVL 树的根是多少。

数据范围
1≤N≤20
输入样例1：
5
88 70 61 96 120
输出样例1：
70
输入样例2：
7
88 70 61 96 120 90 65
输出样例2：
88

思想

待补充！！！！

自己的代码

#include<iostream>
using namespace std;
const int N = 100;
int l[N], r[N], h[N], v[N];
int idx = 0;
void update(int u){
    h[u] = max(h[l[u]], h[r[u]]) + 1;
}
void R(int &u){
    int p = l[u];
    l[u] = r[p];
    r[p] = u;
    update(u),update(p);//更新高度
    u = p;//要用引用更新根
}
void L(int &u){
    int p = r[u];
    r[u] = l[p];
    l[p] = u;
    update(u),update(p);
    u = p;
}
int get_balance(int u){
    
    return h[l[u]] - h[r[u]];
}

void insert(int &u, int w){
    if(!u){//第一种情况，一开始u==0， 第二种l[u]或r[u]==0,插入到对应位置 
        u = ++ idx;//注意0位置不存任何东西，0位置时用来表示空的
        v[u] = w;
    }
    else if(w < v[u]){
        insert(l[u], w);
        if(get_balance(u) == 2){
            if(get_balance(l[u]) == 1) R(u);
            else L(l[u]), R(u);
        }
    }
    else{
        insert(r[u], w);
        if (get_balance(u) == -2)
        {
            if(get_balance(r[u]) == -1) L(u);//注意这里是-1
            else R(r[u]), L(u);
        }
    }
    update(u);//每次插入都要更新h
}

int main(){
    int n;
    cin>>n;
    int u = 0, i, w;
    for(i = 0; i < n; i ++){
        cin>>w;
        insert(u, w);
    }
    cout<<v[u]<<endl;
    
}

y总的代码

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 30;

int l[N], r[N], v[N], h[N], idx;

void update(int u)
{
    h[u] = max(h[l[u]], h[r[u]]) + 1;
}

void R(int& u)
{
    int p = l[u];
    l[u] = r[p], r[p] = u;
    update(u), update(p);
    u = p;
}

void L(int& u)
{
    int p = r[u];
    r[u] = l[p], l[p] = u;
    update(u), update(p);
    u = p;
}

int get_balance(int u)
{
    return h[l[u]] - h[r[u]];
}

void insert(int& u, int w)
{
    if (!u) u = ++ idx, v[u] = w;
    else if (w < v[u])
    {
        insert(l[u], w);
        if (get_balance(u) == 2)
        {
            if (get_balance(l[u]) == 1) R(u);
            else L(l[u]), R(u);
        }
    }
    else
    {
        insert(r[u], w);
        if (get_balance(u) == -2)
        {
            if (get_balance(r[u]) == -1) L(u);
            else R(r[u]), L(u);
        }
    }

    update(u);
}

int main()
{
    int n, root = 0;
    cin >> n;

    while (n -- )
    {
        int w;
        cin >> w;
        insert(root, w);
    }

    cout << v[root] << endl;

    return 0;
}

作者：yxc
链接：https://www.acwing.com/activity/content/code/content/283632/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

判断完全AVL树

题目

AVL树是一种自平衡二叉搜索树。

在AVL树中，任何节点的两个子树的高度最多相差 1 个。

如果某个时间，某节点的两个子树之间的高度差超过 1，则将通过树旋转进行重新平衡以恢复此属性。

图 1?4 说明了旋转规则。

1.jpg 2.jpg
3.jpg 4.jpg

现在，给定插入序列，请你输出得到的AVL树的层序遍历，并判断它是否是完全二叉树。

输入格式
第一行包含整数 N，表示插入序列中元素个数。

第二行包含 N 个不同的整数表示插入序列。

输出格式
第一行输出得到的AVL树的层序遍历序列。

第二行，如果该AVL树是完全二叉树，则输出 YES，否则输出 NO。

数据范围
1≤N≤20
输入样例1：
5
88 70 61 63 65
输出样例1：
70 63 88 61 65
YES
输入样例2：
8
88 70 61 96 120 90 65 68
输出样例2：
88 65 96 61 70 90 120 68
NO
难度：中等
时/空限制：0.4s / 64MB
总通过数：374
总尝试数：634
来源：PAT甲级真题1123
算法标签

代码

#include <iostream>

using namespace std;

const int N = 30;

int n;
int l[N], r[N], v[N], h[N], idx;
int q[N], pos[N];

void update(int u)
{
    h[u] = max(h[l[u]], h[r[u]]) + 1;
}

void R(int& u)
{
    int p = l[u];
    l[u] = r[p], r[p] = u;
    update(u), update(p);
    u = p;
}

void L(int& u)
{
    int p = r[u];
    r[u] = l[p], l[p] = u;
    update(u), update(p);
    u = p;
}

int get_balance(int u)
{
    return h[l[u]] - h[r[u]];
}

void insert(int& u, int w)
{
    if (!u) u = ++ idx, v[u] = w;
    else if (w < v[u])
    {
        insert(l[u], w);
        if (get_balance(u) == 2)
        {
            if (get_balance(l[u]) == 1) R(u);
            else L(l[u]), R(u);
        }
    }
    else
    {
        insert(r[u], w);
        if (get_balance(u) == -2)
        {
            if (get_balance(r[u]) == -1) L(u);
            else R(r[u]), L(u);
        }
    }

    update(u);
}

bool bfs(int root)
{
    int hh = 0, tt = 0;
    q[0] = root;
    pos[root] = 1;

    bool res = true;
    while (hh <= tt)
    {
        int t = q[hh ++ ];
        if (pos[t] > n) res = false;

        if (l[t]) q[ ++ tt] = l[t], pos[l[t]] = pos[t] * 2;
        if (r[t]) q[ ++ tt] = r[t], pos[r[t]] = pos[t] * 2 + 1;
    }

    return res;
}

int main()
{
    int root = 0;
    cin >> n;
    for (int i = 0; i < n; i ++ )
    {
        int w;
        cin >> w;
        insert(root, w);
    }

    bool res = bfs(root);

    cout << v[q[0]];
    for (int i = 1; i < n; i ++ ) cout << ' ' << v[q[i]];
    cout << endl;

    if (res) puts("YES");
    else puts("NO");

    return 0;
}

作者：yxc
链接：https://www.acwing.com/activity/content/code/content/283649/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

判断红黑树

待补充！！！

题目

思想

代码

等重路径

题目

给定一个非空的树，树根为 R。

树中每个节点 Ti 的权重为 Wi。

从 R 到 L 的路径权重定义为从根节点 R 到任何叶节点 L 的路径中包含的所有节点的权重之和。

现在给定一个加权树以及一个给定权重数字，请你找出树中所有的权重等于该数字的路径（必须从根节点到叶节点）。

例如，我们考虑下图的树，对于每个节点，上方的数字是节点 ID，它是两位数字，而下方的数字是该节点的权重。

假设给定数为 24，则存在 4 个具有相同给定权重的不同路径：{10 5 2 7}，{10 4 10}，{10 3 3 6 2}，{10 3 3 6 2}， 已经在图中用红色标出。

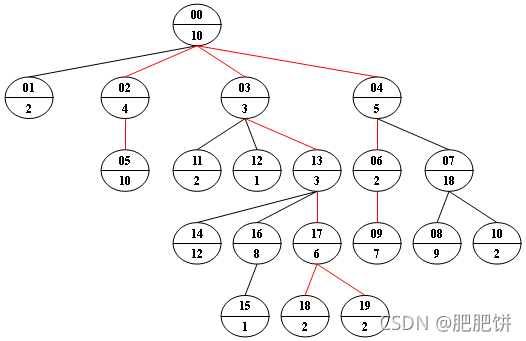
输入格式
第一行包含三个整数 N,M,S，分别表示树的总节点数量，非叶子节点数量，给定权重数字。

第二行包含 N 个整数 Wi，表示每个节点的权重。

接下来 M 行，每行的格式为：

ID K ID[1] ID[2] … ID[K]
ID 是一个两位数字，表示一个非叶子结点编号，K 是一个整数，表示它的子结点数，接下来的 K 个 ID[i] 也是两位数字，表示一个子结点的编号。

出于方便考虑，根节点固定为 00，且树中所有节点的编号为 00～N?1。

输出格式
以单调递减的顺序输出所有权重为S的路径。

每个路径占一行，从根节点到叶节点按顺序输出每个节点的权重。

注意：我们称 A 序列 {A1,A2,…,An} 大于 B 序列 {B1,B2,…,Bm}，当且仅当存在一个整数 k，1≤k<min(n,m)，对于所有 1≤i≤k，Ai=Bi 成立，并且 Ak+1>Bk+1。

数据范围
1≤N≤100,
0≤M<N,
0<S<230,
0<Wi<1000
输入样例：
20 9 24
10 2 4 3 5 10 2 18 9 7 2 2 1 3 12 1 8 6 2 2
00 4 01 02 03 04
02 1 05
04 2 06 07
03 3 11 12 13
06 1 09
07 2 08 10
16 1 15
13 3 14 16 17
17 2 18 19
输出样例：
10 5 2 7
10 4 10
10 3 3 6 2
10 3 3 6 2
难度：中等
时/空限制：0.4s / 64MB
总通过数：504
总尝试数：801
来源：PAT甲级真题1053
算法标签

思想

1、dfs去求

void dfs(int u, int s, vector<int> &path)
{
    bool is_leaf = true;
    for (int i = 0; i < n; i ++ )
        if (g[u][i])
        {
            is_leaf = false;
            break;
        }

    if (is_leaf)
    {
        if (s == S) ans.push_back(path);
    }
    else
    {
        for (int i = 0; i < n; i ++ )
            if (g[u][i])
            {
                path.push_back(w[i]);
                dfs(i, s + w[i], path);
                path.pop_back();
            }
    }
}

2、 从大到小排序，价格后面的greater

vector<vector<int>> ans;

sort(ans.begin(), ans.end(), greater<vector<int>>());

自己的代码

//用vector可以实现如上的比较
//用vector<vector<int>> 来存路径
//判断叶子节点——bool数组，我感觉很多方法都可以
//使用dfs可以搜索从根节点到每一个叶子节点的路径
#include<iostream>
#include <vector>
#include <algorithm>
using namespace std;
const int N = 110;
int w[N];
bool g[N][N];
vector<vector<int>> ans;
int n, m, S;
void dfs(int u, int s, vector<int> &path){
    bool is_leaf = true;
    for(int i = 0; i < n; i ++){
        if(g[u][i]){
            is_leaf = false;
            break;
        }
    }
    if(is_leaf){
        if(s == S)
            ans.push_back(path);
        return;
    }
    else{
        for(int i = 0; i < n; i ++){
            if(g[u][i]){
                path.push_back(w[i]);
                dfs(i,s + w[i],path);
                path.pop_back();
            }
        }
    }
    return;
}
int main(){
    cin>>n>>m>>S;
    for(int i = 0; i < n; i ++) cin>>w[i];
    for(int i = 0; i < m; i ++){
        int id, k;
        cin>>id>>k;
        for(int j = 0; j < k; j ++){
            int child;
            cin>>child;
            g[id][child] = true;
        }
    }
    vector<int> path;
    path.push_back(w[0]);
    dfs(0, w[0], path);
    
    sort(ans.begin(), ans.end(), greater<vector<int>>());//这个greater什么意思？？？？
    
    for(auto an : ans){
        cout<<an[0];
        for(int i = 1; i < an.size(); i ++){
            cout<<" "<<an[i];
        }
        cout<<endl;
    }
}

y总的代码

#include <iostream>
#include <cstring>
#include <vector>
#include <algorithm>

using namespace std;

const int N = 110;

int n, m, S;
int w[N];
bool g[N][N];
vector<vector<int>> ans;

void dfs(int u, int s, vector<int> &path)
{
    bool is_leaf = true;
    for (int i = 0; i < n; i ++ )
        if (g[u][i])
        {
            is_leaf = false;
            break;
        }

    if (is_leaf)
    {
        if (s == S) ans.push_back(path);
    }
    else
    {
        for (int i = 0; i < n; i ++ )
            if (g[u][i])
            {
                path.push_back(w[i]);
                dfs(i, s + w[i], path);
                path.pop_back();
            }
    }
}

int main()
{
    cin >> n >> m >> S;
    for (int i = 0; i < n; i ++ ) cin >> w[i];

    while (m -- )
    {
        int id, k;
        cin >> id >> k;
        while (k -- )
        {
            int son;
            cin >> son;
            g[id][son] = true;
        }
    }

    vector<int> path({w[0]});
    dfs(0, w[0], path);

    sort(ans.begin(), ans.end(), greater<vector<int>>());

    for (auto p : ans)
    {
        cout << p[0];
        for (int i = 1; i < p.size(); i ++ ) cout << ' ' << p[i];
        cout << endl;
    }

    return 0;
}

作者：yxc
链接：https://www.acwing.com/activity/content/code/content/294234/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。