动态规划-01背包

动态规划中最为经典的题目必然就是背包问题, 而背包问题的基础就是01背包.

引用一个大佬梳理的背包图解

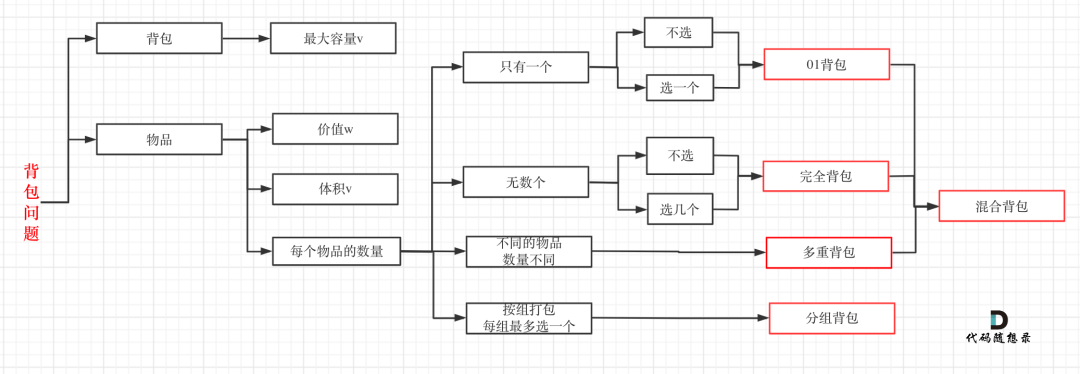
由上图可以看到,01背包其实就是背包选物品,一种物品只有一个,要么选,要么不选.

先通过一个简单的01背包问题来理解01背包问题.

01背包

有N件物品和一个最多能被重量为W 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

| 物品名称 | 价值 | 重量 |
| ----- |:----: |
| 物品0 | 1 | 10 |
| 物品1 | 2 | 15 |
| 物品2 | 51 | 20 |

根据我们上一张总结的动态规划步骤,

第一步:确定dp数组

dp[i][j]：从0到i件物品中选择放入背包容量为j的背包中的最大价值

第二步:递推公式

dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i]] + value[i])
按照题目的描述,一个物品要么选,要么不选,选的话只能选一次物品i不选的情况为dp[i-1][j],物品i选择的情况是dp[i-1][j-weight[i]] + value[i];

第三步:dp数组初始化

物品0放入容量小于它重量的背包的value应该都是0,容量为0的背包放不下任何一件物品.
dp[0][i] = 0;
dp[j][0] = 0;

第四步:确定遍历顺序

遍历的顺序:从前到后遍历

第五步:举例推导dp数组

滚动数组

前面一篇中我们有提到滚动数组,作为优化空间复杂度.

01背包是否可以用滚动数组呢?

当然是可以的,我们可以看到01背包的遍历也是一层一层的往下的

所以公式 dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i]] + value[i]) 好像可以简化成 dp[j] = max(dp[j], dp[j-weight[i]] + value[i]).

有没有感觉有什么不对?

是的, 如果按照二维数组的遍历顺序来执行这个一位数组,会导致被重复的抽取,即从小到大的遍历顺序时,

dp[j] = max(dp[j], dp[j-weight[i]] + value[i]) 等价于二维数组的 dp[i][j] = max(dp[i-1][j], dp[i][j-weight[i]] + value[i])

所以在一维数组的公式下,我们需要以背包容量倒序的顺序进行遍历.

代码实现

func backpack01(arr [][]int, cap int) int {
	if len(arr) == 0 {
		return 0
	}
	x := len(arr)
	dp := make([][]int, x)
	for k := range dp {
		dp[k] = make([]int, cap + 1)
	}
	for i := 0; i < x; i++  {
		dp[i][0] = 0
	}
	for j := 0; j <= cap; j++ {
		if arr[0][0] <= j {
			dp[0][j] = arr[0][1]
		} else {
			dp[0][j] = 0
		}
	}
	var tmp float64
	for i := 1; i < x; i++  {
		for j := 1; j <= cap; j++ {

			if j - arr[i][0] >= 0  {
				tmp = math.Max(float64(dp[i - 1][j]), float64(dp[i - 1][j - arr[i][0]] + arr[i][1]))
			} else {
				tmp = float64(dp[i - 1][j])
			}
			dp[i][j] = int(tmp)
		}
	}
	return dp[x - 1][cap]
}