[数据结构与算法]环形链表——返回环开始的节点

环形链表Ⅱ

解法一：

使用HashSet存储每个节点：

public class Solution {
    public ListNode detectCycle(ListNode head) {
        ListNode node = head;
        HashSet<ListNode> set = new HashSet<ListNode>();
        while (node != null) {
            if (set.contains(node)) {
                return node;
            } else {
                set.add(node);
            }
            node = node.next;
        }
        return null;
    }
}

解法二

使用快慢指针：

public class Solution {
    public ListNode detectCycle(ListNode head) {
        if (head == null || head.next == null)
            return null;

        ListNode slow = head;
        ListNode fast = head;

        while (fast != null && fast.next != null) {
            fast = fast.next.next;
            slow = slow.next;

            if (slow == fast) {	//标记
                slow = head;
                while (slow != fast) {
                    slow = slow.next;
                    fast = fast.next;
                }
                return slow;
            }
        }
        return null;
    }
}

标记处思路解析

假设slow和fast相遇时，slow总共走了k步，那么fast走了2k步，假设圆环长度为h，则k=nh，也就是说，k是h的整数倍，理由如下：

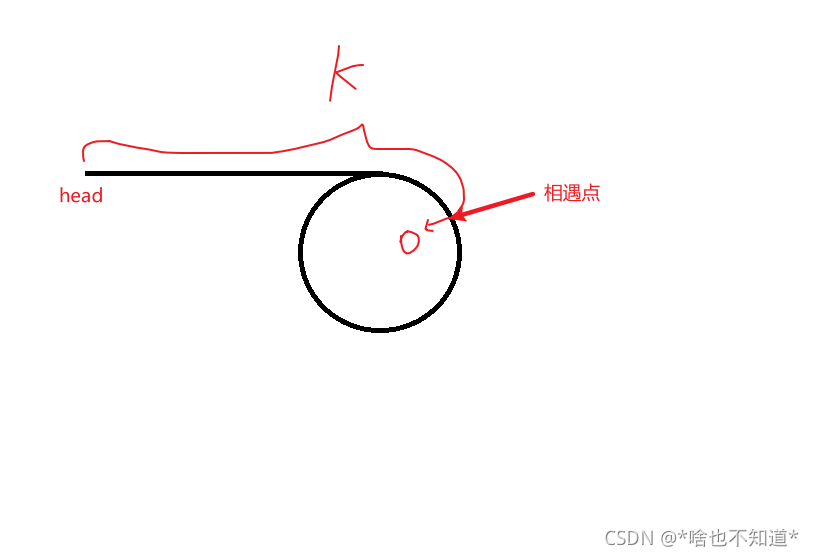
如上图所示，假设slow和fast的相遇点为o，slow和fast同时从head出发，fast先到达o点，然后在环内继续移动，当slow到达o点时，fast刚好也到达，所以fast的第二个k步是在环内o开始，绕环n圈后回到o点产生的，所以k是环长的整数倍。

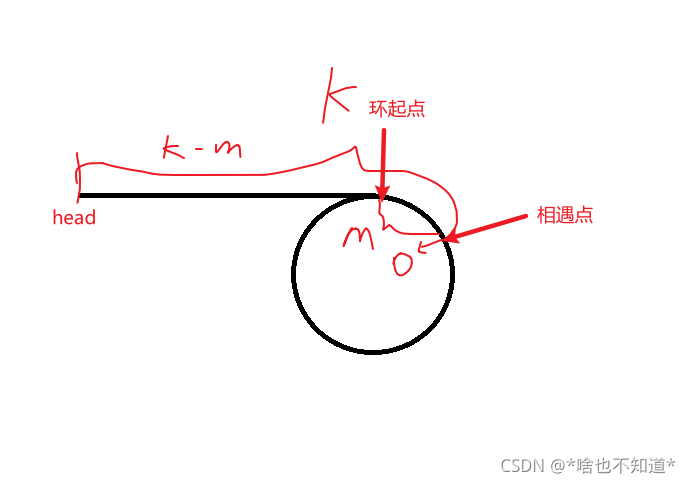
这时假设环起点和相遇点的距离为m，则从head到环起点的距离为k-m，此时令fast从相遇点出发，走k-m步，正好回到了环起点，在fast出发的同时，让slow指针同时从head出发，步幅相同的情况下，当slow == fast时，slow就是环起点。