基本概念
图(Graph)是一种复杂的非线性结构,在图结构中,每个元素都可以有零个或多个前驱,也可以有零个或多个后继,也就是说,元素之间的关系是任意的。
常用术语:
| 术语 | 含义 |
|---|---|
| 顶点 | 图中的某个结点 |
| 边 | 顶点之间连线 |
| 相邻顶点 | 由同一条边连接在一起的顶点 |
| 度 | 一个顶点的相邻顶点个数 |
| 简单路径 | 由一个顶点到另一个顶点的路线,且没有重复经过顶点 |
| 回路 | 出发点和结束点都是同一个顶点 |
| 无向图 | 图中所有的边都没有方向 |
| 有向图 | 图中所有的边都有方向 |
| 无权图 | 图中的边没有权重值 |
| 有权图 | 图中的边带有一定的权重值 |
图的结构很简单,就是由顶点 V 集和边 E 集构成,因此图可以表示成 G = (V,E)
无向图:
若顶点 Vi 到 Vj 之间的边没有方向,则称这条边为无向边 (Edge) ,用无序偶对 (Vi,Vj) 来表示。如果图中任意两个顶点之间的边都是无向边,则称该图为无向图 (Undirected graphs)。
如:下图就是一个无向图,由于是无方向的,连接顶点 A 与 D 的边,可以表示无序队列(A,D),也可以写成 (D,A),但不能重复。顶点集合 V = {A,B,C,D};边集合 E = {(A,B),(A,D),(A,C)(B,C),(C,D),}
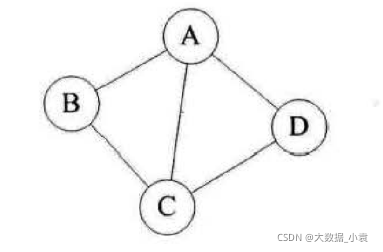
有向图:
用有序偶<Vi,Vj>来表示,Vi 称为弧尾 (Tail) , Vj称为弧头 (Head)。 如果图中任意两个顶点之间的边都是有向边,则称该图为有向图 (Directed grahs)。
如:下图就是一个有向图。连接顶点 A 到 D 的有向边就是弧,A是弧尾,D 是弧头, <A, D>表示弧, 注意不能写成<D,A>。其中顶点集合 V = { A,B,C,D}; 弧集合 E = {<A,D>,<B,A>,<B,C>,<C,A>}
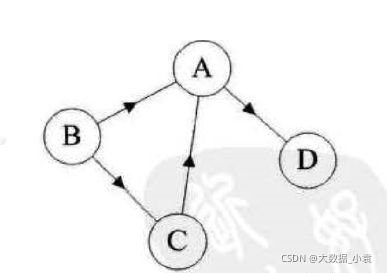
注意:无向边用小括号 “()” 表示,而有向边则是用尖括号"<>"表示
有权图:
有些图的边或弧具有与它相关的数字,这种与图的边或弧相关的数叫做权 (Weight) 。这些权可以表示从一个顶点到另一个顶点的距离或耗费。这种带权的图通常称为网 (Network)。
如下图
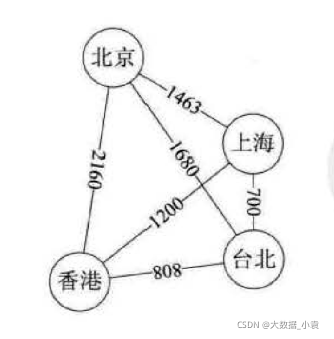
图的存储结构及实现
图结构的常见的两个存储方式: 邻接矩阵 、邻接表
邻接矩阵
 图中的 0 表示该顶点无法通向另一个顶点,相反 1 就表示该顶点能通向另一个顶点
图中的 0 表示该顶点无法通向另一个顶点,相反 1 就表示该顶点能通向另一个顶点
先来看第一行,该行对应的是顶点A,那我们就拿顶点A与其它点一一对应,发现顶点A除了不能通向顶点D和自身,可以通向其它任何一个的顶点
因为该图为无向图,因此顶点A如果能通向另一个顶点,那么这个顶点也一定能通向顶点A,所以这个顶点对应顶点A的也应该是 1
虽然我们确实用邻接矩阵表示了图结构,但是它有一个致命的缺点,那就是矩阵中存在着大量的 0,这在程序中会占据大量的内存。此时我们思考一下,0 就是表示没有,没有为什么还要写,所以我们来看一下第二种表示图结构的方法,它就很好的解决了邻接矩阵的缺陷
代码实现:
- 顶点类
public class Vertex {
private String value;
public Vertex(String value) {
this.value = value;
}
public String getValue() {
return value;
}
public void setValue(String value) {
this.value = value;
}
@Override
public String toString() {
return value;
}
}
- 图类
public class Graph {
private Vertex[] vertex; //顶点数组
private int currentSize; //默认顶点位置
public int[][] adjMat; //邻接表
public Graph(int size) {
vertex = new Vertex[size];
adjMat = new int[size][size];
}
//向图中加入顶点
public void addVertex(Vertex v) {
vertex[currentSize++] = v;
}
//添加边
public void addEdge(String v1, String v2) {
//找出两个点的下标
int index1 = 0;
for (int i = 0; i < vertex.length; i++) {
if (vertex[i].getValue().equals(v1)) {
index1 = i;
break;
}
}
int index2 = 0;
for (int i = 0; i < vertex.length; i++) {
if (vertex[i].getValue().equals(v2)) {
index2 = i;
break;
}
}
//表示两个点互通
adjMat[index1][index2] = 1;
adjMat[index2][index1] = 1;
}
}
- 测试类
public class Demo {
public static void main(String[] args) {
Vertex v1 = new Vertex("A");
Vertex v2 = new Vertex("B");
Vertex v3 = new Vertex("C");
Vertex v4 = new Vertex("D");
Vertex v5 = new Vertex("E");
Graph g = new Graph(5);
g.addVertex(v1);
g.addVertex(v2);
g.addVertex(v3);
g.addVertex(v4);
g.addVertex(v5);
//增加边
g.addEdge("A", "B");
g.addEdge("A", "C");
g.addEdge("A", "E");
g.addEdge("C", "E");
g.addEdge("C", "D");
for (int[] a : g.adjMat) {
System.out.println(Arrays.toString(a));
}
}
}
- 结果值
[0, 1, 1, 0, 1]
[1, 0, 0, 0, 0]
[1, 0, 0, 1, 1]
[0, 0, 1, 0, 0]
[1, 0, 1, 0, 0]
邻接表
邻接表 是由每个顶点以及它的相邻顶点组成的
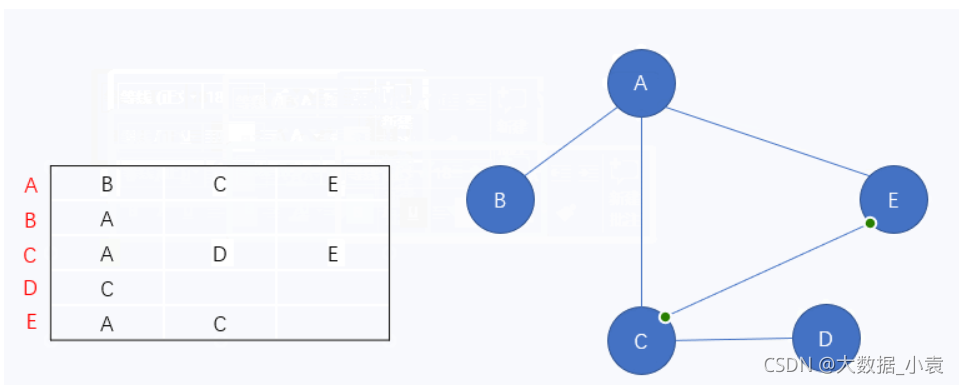
如上图:图中最左侧红色的表示各个顶点,它们对应的那一行存储着与它相关联的顶点
顶点A与 顶点B 、顶点C 、顶点E 相关联顶点B与 顶点A 相关联顶点C与 顶点A 、顶点D 、顶点E 相关联顶点D与 顶点C 相关联顶点E与 顶点A 、顶点C 相关联
图的遍历方式及实现
从图中某一顶点出发访遍图中其余顶点,且使每一个顶点仅被访问一次,这一过程就叫做图的遍历
在图结构中,存在着两种遍历搜索的方式,分别是 广度优先搜索 和 深度优先搜索
广度优先搜索
广度优先遍历(BFS):类似于图的层次遍历,它的基本思想是:首先访问起始顶点v,然后选取v的所有邻接点进行访问,再依次对v的邻接点相邻接的所有点进行访问,以此类推,直到所有顶点都被访问过为止
BFS和树的层次遍历一样,采取队列实现,这里添加一个标记数组,用来标记遍历过的顶点
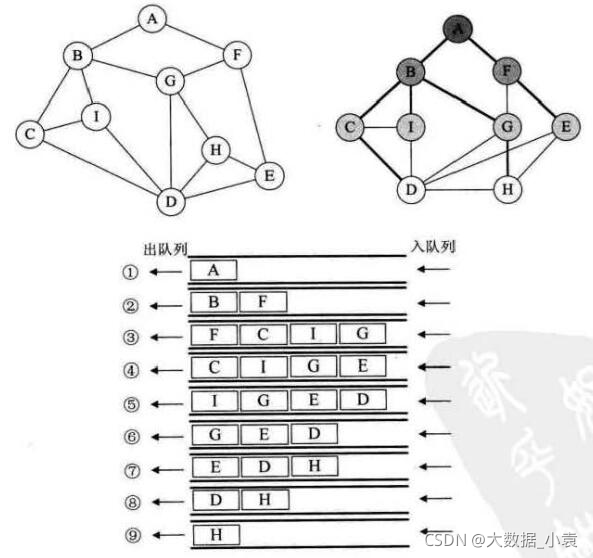
执行步骤:
- 1、先把 A 压入队列,然后做出队操作,A 出队
- 2、把 A 直接相关的顶点 ,B、F 做入队操作
- 3、B 做出队操作,B 相关的点 C、I、G 做入队操作
- 4、F 做出队操作,F 相关的点 E 做入队操作
- 5、C 做出队操作,C 相关的点 D 做入队操作
- 6、I 做出队操作(I 相关的点B、C、D 都已经做过入队操作了,不能重复入队)
- 7、G 做出队操作,G 相关的点 H 做入队操作
- 8、E 做出队操作…
- 9、D 做出队操作…
- 10、H 做出队操作,没有元素了
代码实现:
深度优先搜索
深度优先遍历(DFS):从一个顶点开始,沿着一条路径一直搜索,直到到达该路径的最后一个结点,然后回退到之前经过但未搜索过的路径继续搜索,直到所有路径和结点都被搜索完毕
DFS与二叉树的先序遍历类似,可以采用递归或者栈的方式实现

执行步骤:
- 1、从 1 出发,路径为:
1 -> 2 -> 3 -> 6 -> 9 -> 8 -> 5 -> 4 - 2、当搜索到 4 时,相邻没有发现未被访问的点,此时我们要往后倒退,找寻别的没搜索过的路径
- 3、退回到 5 ,相邻没有发现未被访问的点,继续后退
- 4、退回到 8 ,相邻发现未被访问的点 7,路径为:
8 -> 7 - 5、当搜索到 7 ,相邻没有发现未被访问的点,,此时我们要往后倒退…
- 6、退回路径
7 -> 8 -> 9 -> 6 -> 3 -> 2 -> 1,流程结束
代码实现:
- 栈类
public class MyStack {
//栈的底层使用数组来存储数据
//private int[] elements;
int[] elements; //测试时使用
public MyStack() {
elements = new int[0];
}
//添加元素
public void push(int element) {
//创建一个新的数组
int[] newArr = new int[elements.length + 1];
//把原数组中的元素复制到新数组中
for (int i = 0; i < elements.length; i++) {
newArr[i] = elements[i];
}
//把添加的元素放入新数组中
newArr[elements.length] = element;
//使用新数组替换旧数组
elements = newArr;
}
//取出栈顶元素
public int pop() {
//当栈中没有元素
if (is_empty()) {
throw new RuntimeException("栈空");
}
//取出数组的最后一个元素
int element = elements[elements.length - 1];
//创建一个新数组
int[] newArr = new int[elements.length - 1];
//原数组中除了最后一个元素其他元素放入新数组
for (int i = 0; i < elements.length - 1; i++) {
newArr[i] = elements[i];
}
elements = newArr;
return element;
}
//查看栈顶元素
public int peek() {
return elements[elements.length - 1];
}
//判断栈是否为空
public boolean is_empty() {
return elements.length == 0;
}
//查看栈的元素个数
public int size() {
return elements.length;
}
}
- 顶点类
public class Vertex {
private String value;
public boolean visited; //访问状态
public Vertex(String value) {
super();
this.value = value;
}
public String getValue() {
return value;
}
public void setValue(String value) {
this.value = value;
}
@Override
public String toString() {
return value;
}
}
- 图类
import mystack.MyStack;
public class Graph {
private Vertex[] vertex; //顶点数组
private int currentSize; //默认顶点位置
public int[][] adjMat; //邻接表
private MyStack stack = new MyStack(); //栈
private int currentIndex; //当前遍历的下标
public Graph(int size) {
vertex = new Vertex[size];
adjMat = new int[size][size];
}
//向图中加入顶点
public void addVertex(Vertex v) {
vertex[currentSize++] = v;
}
//添加边
public void addEdge(String v1, String v2) {
//找出两个点的下标
int index1 = 0;
for (int i = 0; i < vertex.length; i++) {
if (vertex[i].getValue().equals(v1)) {
index1 = i;
break;
}
}
int index2 = 0;
for (int i = 0; i < vertex.length; i++) {
if (vertex[i].getValue().equals(v2)) {
index2 = i;
break;
}
}
//表示两个点互通
adjMat[index1][index2] = 1;
adjMat[index2][index1] = 1;
}
//深度优先搜索
public void dfs() {
//把第0个顶点标记为已访问状态
vertex[0].visited = true;
//把第0个的下标放入栈中
stack.push(0);
//打印顶点值
System.out.println(vertex[0].getValue());
//遍历
out:
while (!stack.is_empty()) {
for (int i = currentIndex + 1; i < vertex.length; i++) {
//如果和下一个遍历的元素是通的
if (adjMat[currentIndex][i] == 1 && vertex[i].visited == false) {
//把下一个元素压入栈中
stack.push(i);
vertex[i].visited = true;
System.out.println(vertex[i].getValue());
continue out;
}
}
//弹出栈顶元素(往后退)
stack.pop();
//修改当前位置为栈顶元素的位置
if (!stack.is_empty()) {
currentIndex = stack.peek();
}
}
}
}
- 测试类
import java.util.Arrays;
public class Demo {
public static void main(String[] args) {
Vertex v1 = new Vertex("A");
Vertex v2 = new Vertex("B");
Vertex v3 = new Vertex("C");
Vertex v4 = new Vertex("D");
Vertex v5 = new Vertex("E");
Graph g = new Graph(5);
g.addVertex(v1);
g.addVertex(v2);
g.addVertex(v3);
g.addVertex(v4);
g.addVertex(v5);
//增加边
g.addEdge("A", "B");
g.addEdge("A", "C");
g.addEdge("A", "E");
g.addEdge("C", "E");
g.addEdge("C", "D");
for (int[] a : g.adjMat) {
System.out.println(Arrays.toString(a));
}
//深度优先遍历
g.dfs();
// A
// B
// C
// E
// D
}
}