化繁为简的分治法
1.算法解释
顾名思义,分治问题由“分”(divide)和“治”(conquer)两部分组成,通过把原问题分为子问题,再将子问题进行处理合并,从而实现对原问题的求解。我们在排序章节展示的归并排序就是典型的分治问题,其中“分”即为把大数组平均分成两个小数组,通过递归实现,最终我们会得到多个长度为 1 的子数组;“治”即为把已经排好序的两个小数组合成为一个排好序的大数组,从长度为 1 的子数组开始,最终合成一个大数组。
我们也使用数学表达式来表示这个过程。定义 T(n) 表示处理一个长度为 n 的数组的时间复杂度,则归并排序的时间复杂度递推公式为 T(n) = 2T(n/2) + O(n)。其中 2T(n/2) 表示我们分成了两个长度减半的子问题,O(n) 则为合并两个长度为 n/2 数组的时间复杂度。那么怎么利用这个递推公式得到最终的时间复杂度呢?这里我们可以利用著名的主定理 (Master theorem)求解:
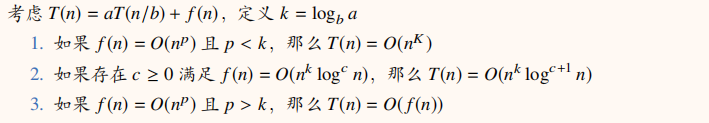
通过主定理我们可以知道,归并排序属于第二种情况,且时间复杂度为 O(n log n)。其他的分治问题也可以通过主定理求得时间复杂度。
另外,自上而下的分治可以和 memoization 结合,避免重复遍历相同的子问题。如果方便推导,也可以换用自下而上的动态规划方法求解。
2.例题
给定一个只包含加、减和乘法的数学表达式,求通过加括号可以得到多少种不同的结果

题解:利用分治思想,可以把加括号转化为,对于每个运算符号,先执行处理两侧的数学表达式,再处理此运算符号。注意边界情况,即字符串内无运算符号,只有数字。
vector<int>diffWaysToCompute(string input)
{
vector<int>ways;
for(int i=0;i<input.length();i++)
{
char c = input[i];
if(c=='+'||c=='-'||c=='*')
{
vector<int>left=diffWaysToCompute(input.sub(0,i));
vector<int>right=diffWaysToCompute(input.sub(i+1));
for(const int & 1:left)
{
for(const int & r:right)
{
switch(c){
case'+':ways.push_back(l+r);break;
case'-':ways.push_back(l-r);break;
case'*':ways.push_back(l*r);break;
}
}
}
}
}
if(ways.empty()) ways.push_back(stoi(input));
return ways;
}
我们发现,某些被 divide 的子字符串可能重复出现多次,因此我们可以用 memoization 来去重。或者与其我们从上到下用分治处理 +memoization,不如直接从下到上用动态规划处理。
vector<int>diffWaysToCompute(string input){
vector<int>data;
vector<char>ops;
int num=0;
char op=' ';
istringstream ss(input + "+");
while(ss>>num&&ss>>op)
{
data.push_back(num);
ops.push_back(op);
}
int n=data.size();
vector<vector<vector<int>>> dp(n,vector<vector<int<<(n,vector<int>()));
for(int i=0;i<n;++i)
{
for(int j=i;j>=0;--j)
{
if(i==j)
{
dp[j][i].push_back(data[i]);
}
else{
for(int k=j;k<i;k+=1)
{
for(auto left : dp[j][k])
{
for(auto right : dp[k+1][i])
{
int val=0;
switch(ops[k])
{
case '+':val=left+right;break;
case '-':val=left-right;break;
case '*':val=left*right;break;
}
dp[j][i].push_back(val);
}
}
}
}
}
}
return dp[0][n-1];
}
上节动态规划还有一解决股票交易问题没写,这里补上:
3.股票交易
题目一:给定一段时间内每天的股票价格,已知你只可以买卖各一次,求最大的收益、
例:输入一个数组,表示每天的股票价格;输出一个整数,表示最大的收益

我们可以遍历一遍数组,在每一个位置 i 时,记录 i 位置之前所有价格中的最低价格,然后将当前的价格作为售出价格,查看当前收益是不是最大收益即可。
int maxProfit(vector<int>&prices)
{
int sell=0,buy=INT_MIN;
for(int i=0;i<prices.size();++i)
{
buy=max(buy,-prices[i]);
sell=max(sell,buy+prices[i]);
}
return sell;
}
题目二:给定一段时间内每天的股票价格,已知你只可以买卖各k次,且每次只能拥有一只股票,求最大的收益。

如果 k 大于总天数,那么我们一旦发现可以赚钱就进行买卖。如果 k 小于总天数,我们可以
建立两个动态规划数组 buy 和 sell,对于每天的股票价格,buy[j] 表示在第 j 次买入时的最大收
益,sell[j] 表示在第 j 次卖出时的最大收益。
//辅函数
int maxProfitUnlimited(vector<int>prices)
{
int maxProfit=0;
for(int i=1;i<prices.size();++i)
{
if(peices[i]>prices[i-1])
{
maxProfit += prices[i] - prices[i-1];
}
}
return maxProfit;
}
//主函数
int maxProfit(int k,vector<int>&prices)
{
int days=prices.size();
if(days<2)
{
return 0;
}
if(k>=days)
{
return maxProfitUnlimited(prices);
}
vector<int>buy(k+1,INT_MIN),sell(k+1,0);
for(int i=0;i<days;++i)
{
for(int j=0;j<=k;++k)
{
buy[j] = max(buy[j],sell[j-1] - prices[i]);
sell[j] = max(sell[j],buy[j] + prices[i]);
}
}
return sell[k];
}
题目三:给定一段时间内每天的股票价格,已知每次卖出之后必须冷却一天,且每次只能拥有一支股票,求最大的收益。

我们可以使用状态机来解决这类复杂的状态转移问题,通过建立多个状态以及它们的转移方式,我们可以很容易地推导出各个状态的转移方程。如图所示,我们可以建立四个状态来表示带有冷却的股票交易,以及它们的之间的转移方式。

int maxProfit(vector<int>&prices)
{
int n=prices.size();
if(n==0){
return 0;
}
vector<int>buy(n),sell(n),s1(n),s2(n);
s1[0]=buy[0]=-prices[0];
sell[0]=s2[0]=0;
for(int i=1;i<n;i++)
{
buy[i]=s2[i-1]-prices[i];
s1[i]=max(buy[i-1],s1[i-1]);
sell[i]=max(buy[i-1],s1[i-1])+prices[i];
s2[i]=max(s2[i-1],sell[i-1]);
}
return max(sell[n-1],s2[n-1]);
}
2021.09.09
滴滴,入职工作5个月零3天了
经验、方法、思考、练习、积累
好好加油,以一个好的面貌迎接2022年!