当你顺利用树的递归解决完了问题,面试官说递归太简单,问你能写一个迭代版本的吗?
那么这个时候,就是到数据结构来模拟jvm帮我们构建的栈的时候啦!
二叉树的前序遍历(※)

思路一:递归
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> res = new LinkedList<>();
if(root == null ) return res;
res.add(root.val);
res.addAll(preorderTraversal(root.left));
res.addAll(preorderTraversal(root.right));
return res;
}
}
思路二:迭代
递归转换为非递归的一个通用方法就是手动模拟栈来维护。
递归的时候jvm帮我们隐式地维护了一个栈,而我们在迭代的时候需要显式地将这个栈模拟出来。
将整棵树的最左边的一条链压入栈 压入栈顶的同时在res链表中加入元素,每一次取出栈顶的元素判断是否有右子树
- 如果有右子树 就将以右子树为根结点的左子树压入栈中 并在结果res中记录 。然后再次取出栈顶的元素,并判断是否有右子树(循环了)
- 如果没有右子树,就继续弹出栈
循环结束的条件就是 当前的指向不为空 或者 是栈不为空
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> res = new LinkedList<>();
if(root == null) return res;
Deque<TreeNode> stack = new LinkedList<>();
while(root != null || !stack.isEmpty()) {
//添加当前结点的左分支
while(root != null){
res.add(root.val);
stack.push(root);
root = root.left;
}
if(!stack.isEmpty()){
TreeNode temp = stack.pop();
root = temp.right;
}
}
return res;
}
}
二叉树的中序遍历(※)

思路一 : 递归写法
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new LinkedList<>();
if(root == null) return res;
//先遍历左子树
res.addAll(inorderTraversal(root.left));
//再加入根
res.add(root.val);
//在遍历右子树
res.addAll(inorderTraversal(root.right));
return res;
}
}
思路二:迭代写法
由于使用迭代的写法,用来内存的栈一层层的调用,现在不让使用递归的方式,那么就自己模拟写一个栈来进行入栈和出栈的操作。
自定义栈的方式来模拟迭代的写法非常常见,一定要掌握!
将整棵树的最左边的一条链压入栈,每一次取出栈顶的元素,加入结果集中,并判断是否有右子树
- 如果有右子树 就将以右子树为根结点的左子树压入栈中。然后再次取出栈顶的元素,加入结果集中并判断是否有右子树(循环了)
- 如果没有右子树,就继续弹出栈
循环结束的条件就是 当前的指向不为空 或者 是栈不为空
上面的这个逻辑写成代码,我觉得还是有一点点难得,转换的时候要仔细想一想
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> list = new LinkedList<>();
Deque<TreeNode> stack = new LinkedList<>();
while(root != null || stack.size() != 0){
while(root != null){
stack.push(root);
root = root.left;
}
//将当前的根加入list 同时判断是否有右结点
TreeNode temp = stack.pop();
list.add(temp.val);
if(temp.right != null){
root = temp.right;
}
}
return list;
}
}
二叉树的后序遍历 (※)

思路一:递归
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
LinkedList<Integer> res = new LinkedList<>();
if(root == null) return res;
res.addAll(postorderTraversal(root.left));
res.addAll(postorderTraversal(root.right));
res.add(root.val);
return res;
}
}
思路二:迭代
手动构建一个栈,对这颗树进行前序遍历,将前序遍历的结果压栈,之后对栈顶的结点进行判断。
- 该节点没有右子树 那么这个结点就是根节点了,可以直接添加
- 该节点有右子树,需要先去添加它的右子树。让指针指向它的右子树,然后在对他的右子树进行前序遍历压栈,取栈顶,判断这样的循环的操作。
当前元素加入res 的标准是 当前结点的右子树为空 || 当前结点的右子树已经添加到结果集了。

但是这里面有一个坑就是要记录当前节点的右子树是否添加过的状态
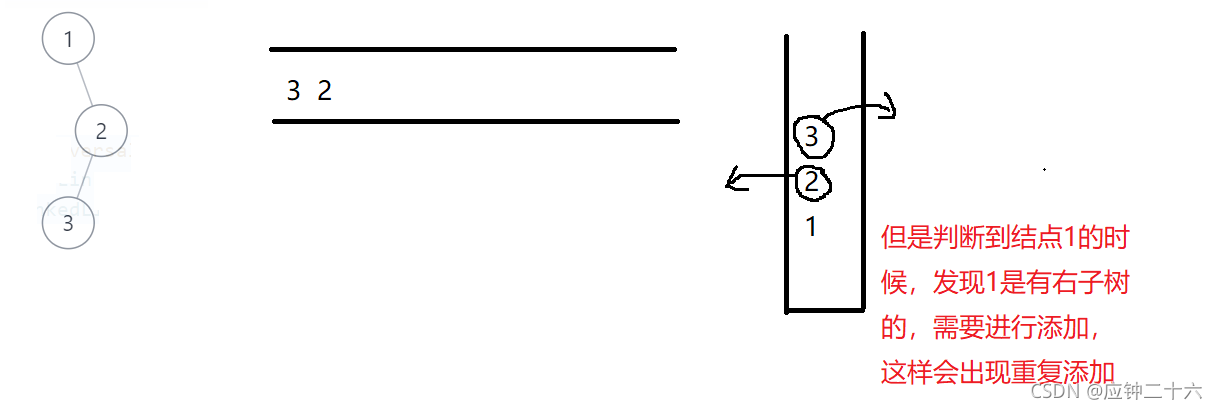
所以解决的办法就是:只要有元素添加到list 中 ,就记录这个结点,就表明这以这个结点为根的子树都已经添加过了。
下次对某一个结点的右子树进行添加的时候,判断一下右节点是不是刚刚加入过list中即可。
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
Deque<TreeNode> stack = new LinkedList<>();
List<Integer>list = new LinkedList<>();
TreeNode prev = null;//prev 用来指向以当前结点为根节点的子树已经添加过了
while(root != null || stack.size() != 0){
//进行前序遍历放所有的左子树
while(root != null ){
stack.push(root);
root = root.left;
}
TreeNode temp = stack.peek();
if(temp.right != null && temp.right != prev){
//当前的结点是有右子树的 并且没有添加过
root = temp.right;
}else{
//出栈 同时进行标记 添加的元素
list.add(stack.pop().val);
prev = temp;//这里进行标记 list 最近一次添加的元素 表示以当前结点的为根的子树都添加过了
}
}
return list;
}
}
二叉树的层序遍历

思路一:
借助队列的方式 拖动结点的左右孩子。
不断的新建临时的list,但是通过循环控制list里面添加的数量。
堆列没有拖动孩子之前队列中的元素的个数 就是当前的temp 中的个数!
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> res = new LinkedList<>();
Queue<TreeNode> queue = new LinkedList<>();
if(root == null) return res;
queue.add(root);
while(!queue.isEmpty()){
List<Integer> temp = new LinkedList<>();
int size = queue.size();//获得没有拖动孩子时候的队列个数
//控制当前的temp 里面添加的元素个数
for(int i = 0; i<size;i++){
TreeNode node = queue.remove();
temp.add(node.val);
if(node.left != null){
queue.add(node.left);
}
if(node.right != null){
queue.add(node.right);
}
}
res.add(temp);
}
return res;
}
}
思路二:带结点数字的的层序遍历
判断当前结点的序号 是不是已经等于res列表中的size个数 如果等于就新建立一个temp。
当开始 第零层 res 的size是0 相等 创立一个temp ,并加入list 它的左右孩子就是 第一层
遍历到第一层的第一个元素时 res 的size 是1 当前的level 也是1 于是在res中创建第二个temp 并加入当前元素。
遍历到第一层的第二个元素时 res的size是 2 当前的level 是1 于是拿出最后最后一个temp 加入。
遍历到第二层第一个元素时 res 的size 是2 当前的level 也是2 于是在res中创建第三个temp 并加入当前元素。
遍历到第二层的第二个元素时 res的size是 3 当前的level 是2 于是拿出最后最后一个temp 加入。
…
class Solution {
//自定义了一个带层级的类
//这个val表示的是当前遍历的是第几层
class NT{
TreeNode node;
int val;
public NT(TreeNode node, int val) {
this.node = node;
this.val = val;
}
}
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> res = new LinkedList<>();
//建立一个队列辅助完成二叉树的层序遍历
Queue<NT> queue = new LinkedList<>();
if(root == null) return res;
queue.add(new NT(root,0));
while(!queue.isEmpty()){
NT cur = queue.poll();
int level = cur.val;
TreeNode node = cur.node;
if(level == res.size()){
//在总的结果中添加list
res.add(new ArrayList<>());
}
//拿到对应的内层的list
List<Integer> innerList = res.get(level);
innerList.add(node.val);
//把它的两个孩子拖动进来
if(node.left != null){
queue.add(new NT(node.left,level+1));
}
if(node.right != null){
queue.add(new NT(node.right,level+1));
}
}
return res;
}
}