Prim算法
算法思想:从图中任意取出一个顶点,把它当成一颗树,然后从与这棵树相连接的边中选取一条最短的(权值最小)的边,并将这条边及其所连接的顶点并入到当前树中。
生成树生成过程
候选边长的算法:此时树中只有0这个顶点,与0相连接的顶点分别为1、2、3长度分别为5、1、2这个长度就是候选边的边长,如果后续有其他顶点加入到生成树中,也需要把新加入的顶点可能到达的边加入到候选边长中。
一、如图a所示,先选取点0,然后选取候选边的边长分别为5、1和2,最小边长为1;
二、如图b所示,选取边长为1的边,此时候选边长分别为5、3、2、6和2,最小边长为2;

三、如图c所示,选取边长为2的边,此时候选边的边长分别为5、3、2和3,其中最小边长为2;
四、选取边长为2的边,此时候选边长分别为3、4、5、,其中最小边长为3

五、选取边长为3的边,此时所有顶点都已并入树中,生成树求解完毕

Prime算法执行过程
从树中某一个顶点v0开始,构造生成树的算法执行过程如下:
1)将v0到其他顶点的所有边当作候选边;
2)重复以下步骤n-1次,使得其他n-1个顶点被并入到生成树中。
- 从候选边中挑选出权值最小的边输出,并将与该边另一端相接的顶点v并入到生成树中;
- 考察所有剩余顶点vi,如果(v,vi)的权值比lowcost[vi],则用(v,vi)的权值更新lowcost[vi]
Prime算法代码
void Prim(MGraph g, int v0, int &sum) {
int lowcost[maxSize], vset[maxSize], v;
int i, j, k, min;
v = v0;
for (i = 0; i < g.n; ++i) {
lowcost[i] = g.edges[v0][i];
vset[i] = 0;
}
vset[v0] = 1; // 将v0并入树中
sum = 0; // sum清零用来累计树的权值
for (i = 0; i < g.n-1; ++i) {
min = INF; // INF是一个已经定义的比图中所有边权值都大的常量
// 下面这个循环用于选出候选边中的最小者
for (j = 0; j < g.n; ++j) {
if (vset[j] == 0 && lowcost[j] < min) { // 选出当前生成树其他顶点到最短边中最短的一条
min = lowcost[j];
k = j;
}
vset[k] = 1;
v = k;
sum += min; // 这里用sum记录了最小生成树的权值
// 下面这个循环以刚进入的顶点v为媒介更新候选边
for (j = 0; j < g.n; ++j) {
if (vset[j] == 0 && g.edges[v][j] < lowcost[j]) {
lowcost[j] = g.edges[v][j];
}
}
}
}
}
Kruskal算法
每次找出候选边中权值最小的边,就将改变并入生成树中。重复直至所有边都被检测完
Kruskal算法执行过程
总思想:每次找到候选边中权值最小的边,将该边并入到生成树中。- 先找到图a中权值最小的边为1
- 将权值为1的边两端连接并入到生成树中,查找到下一个最小的权值为2

- 此时有两个权值为2的边,将其中一个与生成树进行连接,我选择的是2-4这条边,0-3这条边也可以。再次查找到最小的权值为2
- 将权值为2的边与生成树进行连接,此时还剩下点1,点1能连接到生成树中的最小边长为3

- 将点1与生成树进行连接,最后所有的点都并入到生成树中,算法结束。

相关存储结构
| 数组下标 | 边的信息 | 边的权值 |
|---|---|---|
| 0 | (0,1) | 5 |
| 1 | (0,2) | 1 |
| 2 | (0,3) | 2 |
| 3 | (1,2) | 3 |
| 4 | (2,3) | 6 |
| 5 | (1,4) | 4 |
| 6 | (2,4) | 2 |
| 7 | (3,4) | 3 |
Kruskal算法代码
typedef struct {
int a, b; // a和b为一条边所连的两个顶点
int w; // 边的权值
}Road;
Road road[maxSize];
int v[maxSize]; // 定义并查集数组
int getRoot(int a) { //取根节点
while (a != v[a]) // 在并查集中查找根结点的函数
a = v[a]; //当a等于v[a]时找到根节点
return a;
}
根据下图所示,只有根节点结点与上一个结点相同,即0为根节点
| 结点 | 上一个节点 |
|---|---|
| 0 | 0 |
| 1 | 2 |
| 2 | 0 |
| 3 | 0 |
| 4 | 2 |

void Kruskal(MGraph g, int &sum, Road road[]) {
int i, N, E, a, b;
N = g.n;
E = g.e;
sum = 0;
for (i = 0; i < N; ++i) v[i] = i;
sort(road, E); // 对road数组中的E条边按其权值从小到大排序, 假设该函数已定义好
for (i = 0; i < E; ++i) {
a = getRoot(road[i].a);
b = getRoot(road[i].b);
if (a != b) {
v[a] = b;
sum += road[i].w;
}
}
}
Dijkstra算法
Dijkstra算法代码
void Dijkstra(MGraph g, int v, int dist[], int path[]) {
int set[maxSize];
int min, i, j, u;
// 从这句开始对各数组进行初始化
for (i = 0; i < g.n; ++i) {
dist[i] = g.edges[v][i];
set[i] = 0;
if (g.edges[v][i] < INF)
path[i] = v;
else {
path[i] = -1;
}
}
set[v] = 1; path[v] = -1;
// 初始化结束
// 关键操作开始
for (i = 0; i < g.n-1; ++i) {
min = INF;
// 这个循环每次从剩余顶点中选出一个顶点,通往这个顶点的路径在通往所有剩余顶点的路径中是长度最短的
for (j = 0; j < g.n; ++j) {
if (set[j] == 0 && dist[j] < min) {
u = j;
min = dist[j];
}
}
set[u] = 1; // 将选出的顶点并入最短路径中
// 这个循环以刚并入的顶点作为中间点,对所有通往剩余顶点的路径进行检测
for (j = 0; j < g.n; ++j) {
// 这个if语句判断顶点u的加入是否为出现通往顶点j的更短的路径
if (set[j] == 0 && dist[u]+g.edges[u][j] < dist[j]) {
dist[j] = dist[u] + g.edges[u][j];
path[j] = u;
}
}
}
}
Floyd算法
Floyd算法代码
void Floyd(MGraph g, int Path[][maxSize]) {
int i, j, k;
int A[maxSize][maxSize];
// 这个双循环对数组A[][]和Path[][]进行了初始化
for (i = 0; i < g.n; ++i) {
for (j = 0; j < g.n; ++j) {
A[i][j] = g.edges[i][j];
Path[i][j] = -1;
}
}
// 下面三层循环是主要操作,完成了以k为中间点对所有的顶点对{i, }进行检测和修改
for (k = 0; k < g.n; ++k) {
for (i = 0; i < g.n; ++i) {
for (j = 0; j < g.n; ++j) {
if (A[i][j] > A[i][k] + A[k][j]) {
A[i][j] = A[i][k] + A[k][j];
Path[i][j] = k;
}
}
}
}
}
AOV网
Aov网是一种以顶点表示活动、以边表示活动先后次序且没有回路的有向图
在一个有向图中找到拓扑排序的过程如下:
① 从有向图中选择一个没有前驱(入度为零)的顶点输出;
② 删除①中的顶点,并删除剩余图中从该顶点发出的全部边;
③重复上述两步,直到剩余的图中不存在没有前驱的顶点为止。
下面来举个例子:
某产品生产过程如图所示: 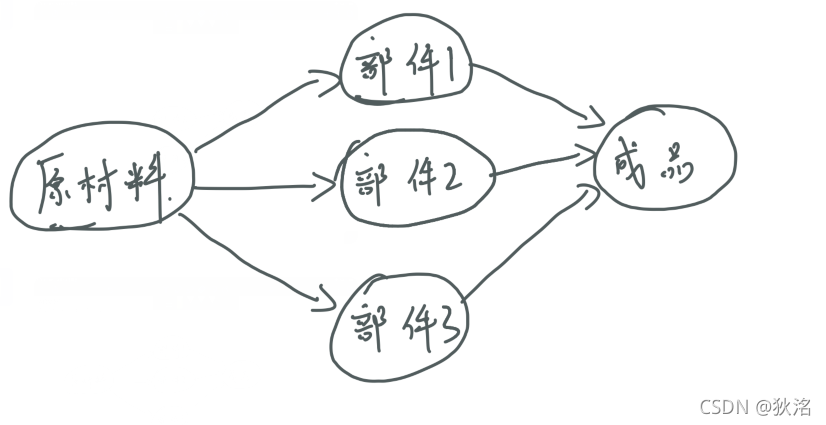-
先找到入度为零的顶点,即为原材料顶点,删除该顶点,并删除该顶点出发的所有边

-
这时会发现部件1、部件2、部件3入度都为0,这时可以选择这三个中的任意一个,我选择的部件1

按照上边1、2两步删除部件2,部件3

拓扑排序中对邻接表表头结构的修改
typedef struct {
char data;
int count; // 此处为新增代码,count用来统计顶点当前的入度
ArcNode *firstarc;
}VNode;
拓扑排序算法代码
【分析】:先找到所有入度为0的顶点,将它们压入入stack[ ]栈中,然后出栈,出栈时将以此次出栈点为firstarc的顶点的入度全部减1,再次进行遍历,查看是否有新的入度为0的顶点,如果有就将它入栈
int TopSort(AGraph *G) { //使用指针是为了避免整个图的复制
int i, j, n = 0; //n 是用于统计输出顶点的个数
int stack[maxSize], top = -1; // 定义并初始化栈、栈中保存所有入度为0的顶点
ArcNode *p;
// 这个循环将图中入度为0的顶点入栈
for (i = 0; i < G->n; ++i) { // 图中的顶点从0开始编号
if (G->adjlist[i].count == 0) {
stack[++top] = i;
}
}
// 关键操作开始
while (top != -1) {
i = stack[top--]; // 顶点出栈
++n; // 计数器加1,统计当前顶点
cout << i << " "; // 输出当前顶点
p = G->adjlist[i].firstarc;
// 这个循环实现了将所有由此顶点引出的边所指向的顶点的入度都减少1
// 并将这个过程中入度变为0的顶点入栈
while (nullptr != p) {
j = p->adjvex;
--(G->adjlist[j].count);
if (G->adjlist[j].count == 0)
stack[++top] = j;
p = p->nextarc;
}
}
// 关键操作结束
return n == G->n;
}