以邻接矩阵作为存储结构存储下面无向图,采用深度优先或广度优先遍历,输出图的所有顶点的值。
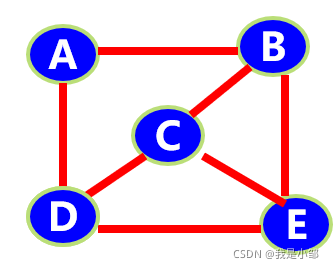
**
程序代码:
**
#include<iostream>
using namespace std;
#define MaxInt 32767
#define MVNum 100
#define OK 1
typedef int Status;
typedef char VerTexType;//顶点数据类型
typedef int ArcType; //边的权值类型
int visited[MVNum];
typedef struct {
VerTexType vexs[MVNum];//顶点表
ArcType arcs[MVNum][MVNum];//邻接矩阵
int vexnum,arcnum;//图的当前点数和边数
} AMGraph;
int LocateVex(AMGraph G,VerTexType u) {
//存在则返回u在顶点表中的下标;否则返回-1
int i;
for(i=0; i<G.vexnum; ++i) {
if(u==G.vexs[i])
return i;
}
return -1;
}
Status CreateUDN(AMGraph &G) {
int i,j,k;
char v1,v2;
cin>>G.vexnum>>G.arcnum; //输入总顶点数,总边数
for(i = 0; i<G.vexnum; ++i)
cin>>G.vexs[i]; //依次输入点的信息
for(i = 0; i<G.vexnum; ++i) {
for(j = 0; j<G.vexnum; ++j)
G.arcs[i][j] = 0;
} //初始化邻接矩阵,边的权值均置为极大值
for(k = 0; k<G.arcnum; ++k) { //构造邻接矩阵
cin>>v1>>v2; //输入一条边依附的顶点及权值
i = LocateVex(G, v1);
j = LocateVex(G, v2); //确定v1和v2在G中的位置
G.arcs[i][j] = 1; //边<v1, v2>的权值置为w
G.arcs[j][i] = G.arcs[i][j];//置<v1, v2>的对称边<v2, v1>的权值为w
}
return OK;
}
void DFS(AMGraph G, int v) { //深度优先搜索,图G为邻接矩阵类型,v为访问顶点元素对应数组下标
cout<<G.vexs[v];//输出下标对应的顶点元素值
visited[v] = true;//访问第v个顶点
for(int w = 0; w< G.vexnum; w++) { //依次检查邻接矩阵v所在的行
if((G.arcs[v][w]!=0)&& (!visited[w]))
DFS(G, w); //w是v的邻接点,如果w未访问,则递归调用DFS
}
}
void PrintAMGraph(AMGraph G) {//输出邻接矩阵
int i,j;
for(i=0; i<G.vexnum; i++) {
for(j=0; j<G.vexnum; j++) {
cout<<G.arcs[i][j]<<' ';
}
cout<<endl;
}
}
int main() {
AMGraph G;
cout<<"创建无向图,请依次输入顶点数,边数,顶点值,每条边关联的顶点"<<endl;
CreateUDN(G);
cout<<"无向图对应邻接矩阵为:"<<endl;
PrintAMGraph(G);
cout<<"请输入要深度遍历的起始顶点值:"<<endl;
VerTexType V;
cin>>V;
int k = LocateVex(G, V);//获取初始遍历顶点元素值
cout<<"深度优先遍历结果为:"<<endl;
DFS(G, k);
return 0;
}
运行截图:

总结:
1,邻接矩阵表示法的优点:直观、简单、好理解,方便检查任意一对顶点间是否存在边,方便找任一顶点的所有“邻接点”(有边直接相连的顶点),方便计算任一顶点的“度”。
2,邻接矩阵表示法的缺点:判断两顶点间是否有边或弧,需搜索两结点对应的单链表,没有邻接矩阵方便。
3,邻接表中每个链表对应于邻接矩阵中的一行,链表中结点个数等于一行中非零元素的个数。
4,对于任一确定的无向图,邻接矩阵是唯一的(行列号与顶点编号一致),但邻接表不唯一(链接次序与顶点编号无关)。空间复杂度:邻接矩阵为O(n2),有向和无向图的邻接表O(n+e)和O(n+2e)。
5,邻接矩阵多用于稠密图,而邻接表多用于稀疏图。
6,深度优先搜索:从同一顶点起始深度遍历的结果不一定唯一访问完当前结点访问其邻接点,访问每个顶点的判断和操作方法相同。
7,广度优先搜索:从图的某一结点出发,首先依次访问该结点的所有邻接点V1,V2,…Vn,再按这些顶点被访问的先后次序依次访问与它们相邻接的所有未被访问的顶点,重复此过程直至所有顶点均被访问位置。